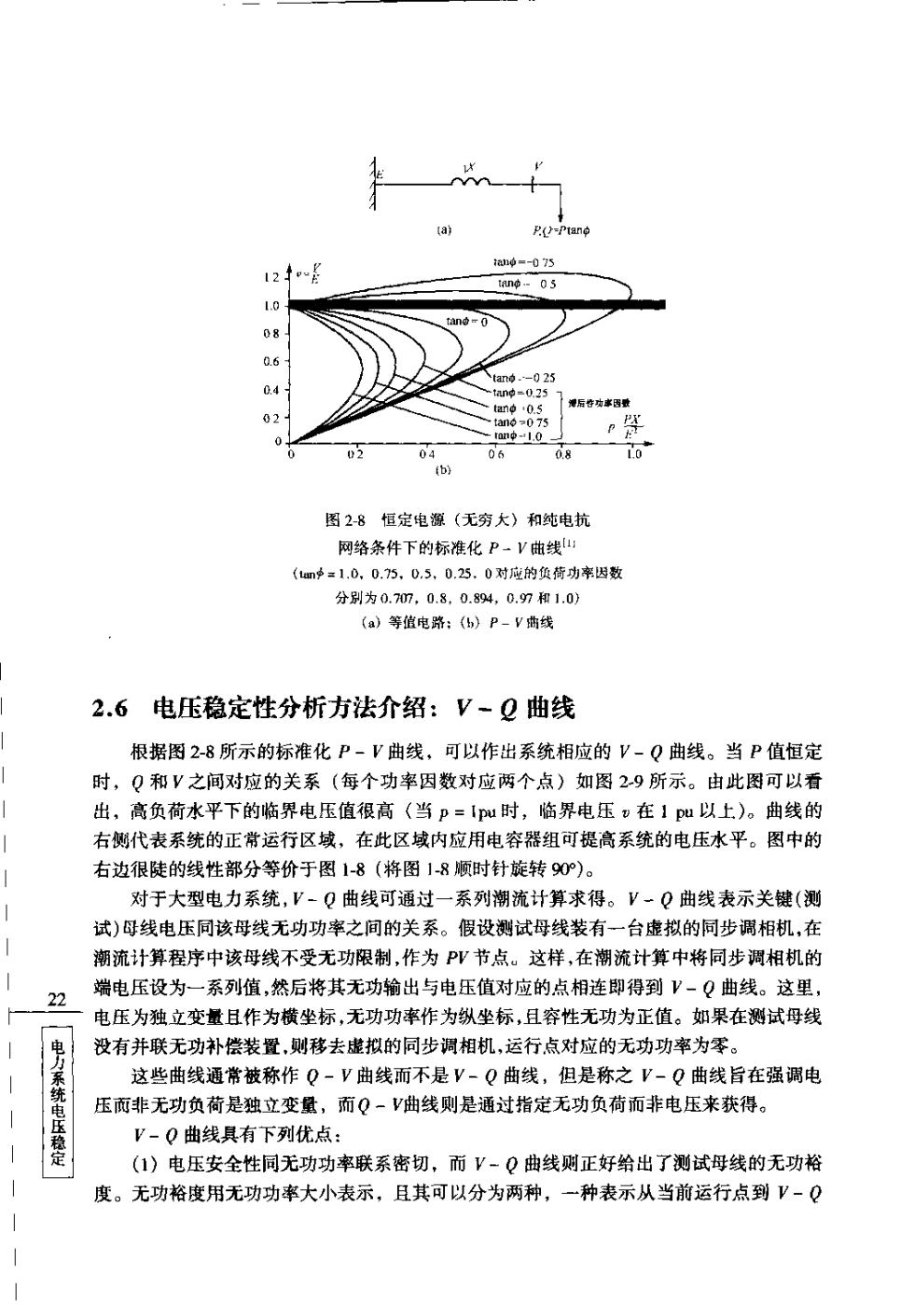
12 L.C ib) 图2-8恒定电源(无穷大)和纯电抗 网络条件下的标准化P一V曲线 (m=1.00.5.0,5.0.25.0对应的负荷功辛因数 分别为0.7m.0.8.0.4,0.97和1.0 (a)等值电路:(h)P-V线 2.6电压稳定性分析方法介绍:V-Q曲线 根据图2-8所示的标准化P-V曲线,可以作出系统相应的V-Q曲线。当P值恒定 时,Q和V之间对应的关系(每个功率因数对应两个点)如图29所示。由此图可以看 出,高负荷水平下的临界电压值很高(当p=Iu时,临界电压在1pu以上)。曲线的 右侧代表系统的正常运行区域,在此区域内应用电容器组可提高系统的电压水平。图中的 右边很陡的线性部分等价于图1-8(将图1-8顺时针旋转90)。 对于大型电力系统,V-Q曲线可通过一系列潮流计算求得。V一Q曲线表示关键(测 试)母线电压同该母线无功功率之间的关系。假设测试母线装有一台虚拟的同步调相机,在 潮流计算程序中该母线不受无功限制,作为PΨ节点。这样,在潮流计算中将同步调相机的 22 端电压设为一系列值,然后将其无功输出与电压值对应的点相连即得到V-Q曲线。这里 电压为独立变量且作为横坐标,无功功率作为纵坐标,且容性无功为正值。如果在测试母线 没有并联无功补偿装置,则移去虚拟的同步调相机,运行点对应的无功功率为零。 这些曲线通常被称作Q-V曲线而不是V-Q曲线,但是称之V-Q曲线旨在强调电 压而非无功负荷是独立变量,而Q-V曲线则是通过指定无功负荷而非电压来获得。 电压稳定 V-Q曲线具有下列优点: (1)电压安全性同无功功率联系密切,而V-Q曲线则正好给出了测试母线的无功裕 度。无功裕度用无功功率大小表示,且其可以分为两种,一种表示从当前运行点到V-Q
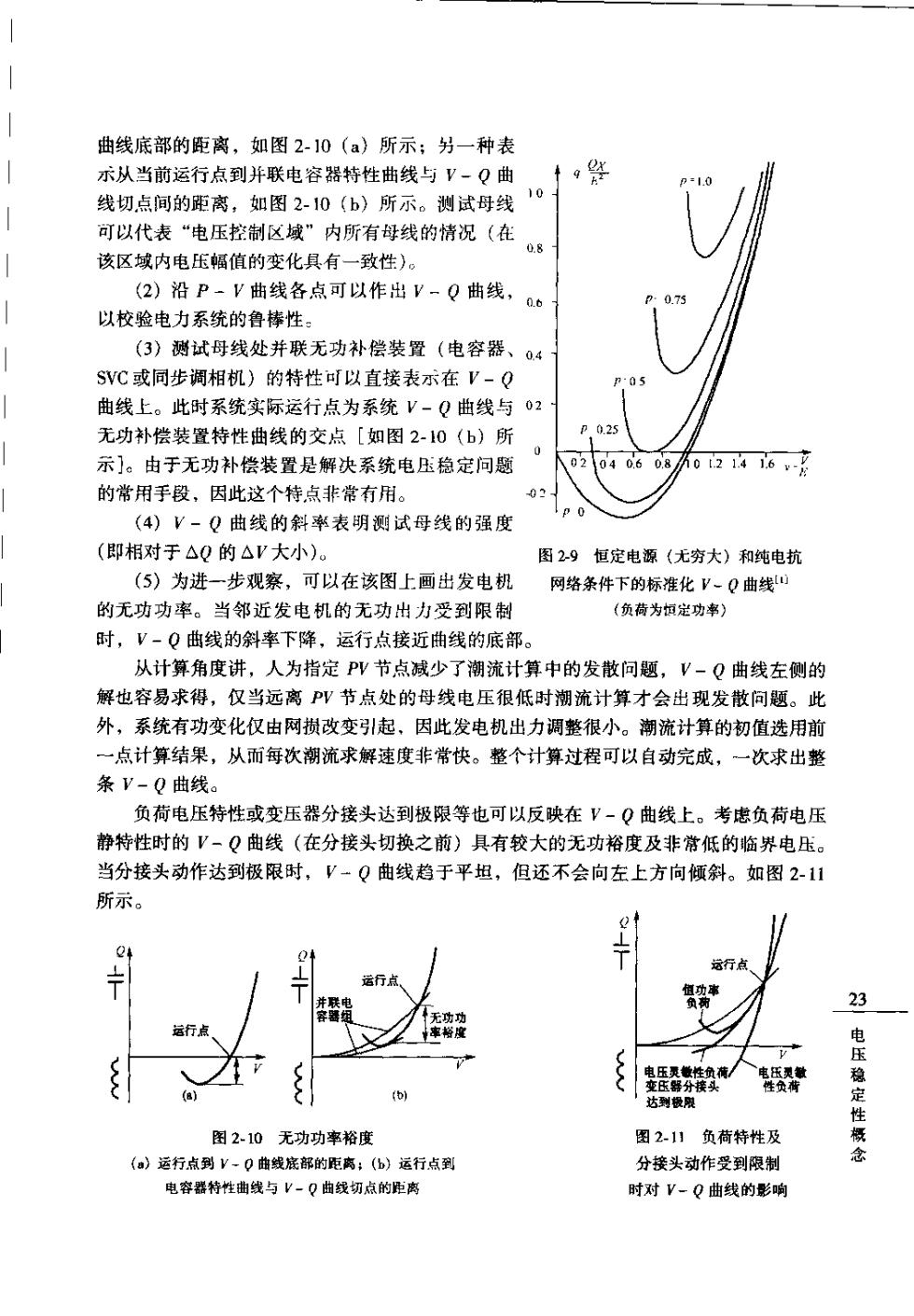
曲线底部的距离,如图2-10(a)所示;另一种表 示从当前运行点到并联电容器特性曲线与V-Q曲 线切.点间的距离,如图2-10(b)所示。测试母线 10 可以代表“电压控制区域”内所有母线的情况(在 该区域内电压幅值的变化具有一致性)。 (2)沿P-V曲线各点可以作出V-Q曲线, 以校验电力系统的鲁棒性」 (3)测试母线处并联无功补偿装置(电容器、Q4 SVC或同步调相机)的特性以直接表示在V-Q 曲线上。此时系统实际运行点为系统V-Q曲线与02 无功补偿装置特性曲线的交点[如图2-10(b)所 示]。由于无功补偿装置是解决系统电压稳定问题 02 10 0121416 的常用手段,因此这个特点非常有用。 -0 (4)V-Q曲线的斜率表明测试母线的强度 (即相对于△Q的△V大小), 图2-9恒定电源(无穷大)和纯电抗 (5)为讲一步现察。可以在该图上画出发电机. 网络条件下的标准化V-Q曲线口 的无功功率。当邻近发电机的无功出力受到限制 负荷为恒定功率) 时,V-O曲线的斜率下降,运行点接近曲线的底部。 从计算角度讲,人为指定PV节点减少了潮流计算中的发散问题,V-Q曲线左侧的 解也容易求得,仅当远离V节点处的母线电压很低时潮流计算才会出现发散问题。此 外,系统有功变化仅由网损改变引起、因此发电机出力调整很小。潮流计算的初值选用前 一点计算结果,从而每次潮流求解速度非常快。整个计算过程可以自动完成,一次求出整 条V=O曲线 负荷电压特性或变压器分接头达到极限等也可以反映在V-Q曲线上。考虑负荷电压 静特性时的V-Q曲线(在分接头切换之前)具有较大的无功裕度及非常低的临界电压。 当分接头动作达到极限时,V一Q曲线趋于平坦,但还不会向左上方向倾斜。如图2-11 所示。 行 运行点 23 远行点 (a) 图2.10无功功率裕度 图211负荷特性及 (a)运行点到Y-0曲线底部的距离:(6)运行点到 分接头动作受到限制 电容器特性曲线与V一Q曲切点的距离 时对V-Q曲线的影

V-Q曲线现在是许多电力公司分析电压稳定性的主要方法。但因该方法人为地强调 单个母线特性,因而所得结论应用更切合实际的方法来验证。 2.7长期电压稳定图释 本节应用P-V曲线揭示与负荷特性相关的电压稳定性,同时研究变压器分接头调 整、恒能负荷(d)与发电机电流限制环节的影响。 图212表示一个示例系统。当电压变化范围在0.9一1.1u时,假设感应电动机为恒 功率静态负荷,且感应电动机无功需求由并联无功补偿装置提供。考虑不同比例的恒功率 与恒电阻负荷(在较小的电压变化范围内,其他负荷成分诸如照明设备可以用恒功率与恒 电阻负荷的组合表示),负荷电阻(对应电导G)通过乘以TC变压器变比n的平方折算 到输电线路侧。变压器分接头的调整范!制为±10% 阁212系统示意图 考虑两种极端的负荷组成情况,一种情祝为75%感应电动机负荷加25%恒电阻负荷。 近似表示工业负荷区域,或者具有大量空调的负荷区域:另一种情况为25%感应电动机 负荷加5%恒电阻负荷,近似表示具有大量加热器用户的负荷区域 高比例电动机负荷 图2-13给出3种系统特性曲线,以及含75%电动机时的负荷特性曲线,运行点为系 统特性曲线与负荷特性曲线的交点。 3种系统特性曲线分别代表:①扰动前的系统特性;②故障后发电机电流未受限制 情况下的系统特性;③扰动后某些发电机电流越限情况下的系统特性6,。发电机过载 条件下的励磁电流限制通过过励磁限制器动作或运行人员干预来实现。每一条系统特性曲 24 线都有一个最大功率点,表示发电和输电系统的稳态功率传输能力。这里,系统特性曲线 均为定性描述。 图2-13同时给出了两条含75%感应电动机时的负荷特性曲线,其中一条对应于初始 系统电压 负荷特性,另一条则为变压器分接头将变比调高10%时对应的负荷特性。负荷功率方程 表示为P=0.75+0.25n2GW。系统遭受扰动后电压下降,负荷特性曲线将与扰动后的系 统特性曲线相交。随着电压的下降,电阻负荷吸收的功率将减少,直至变压器分接头动作 为止。但是如果没有带分接头调整变压器,或者分接头位置已调整到极限位置,恒温控制 负荷或其他恒能负荷对应的电导随后将会增加

图213表示的负荷特性曲线是相当不利的情况。当考虑变压器分接头动作和发电机 电流限制时,系统将失去运行点(即系统特性曲线和负荷特性曲线无交点)。失去运行点 将导致系统发生电压崩遗。为确定系统动态行为,需采用精确模型(可能包括交流接触器 的动作特性)进行动态仿真。实际上,在用静态分析法所决定的失稳点之前感应电动机可 能已经发生失稳现象6,·。如果扰动类型包含严重的短路故僚,感应电动机不可能重新 加速。虽然如此,图2-13仍有助于从概念上理解长期电压稳定。 7n1 药死终唐贸建程时 0 找动后系统特性 扰动霸呆统特性 05 图213系统特性曲线和含75%电动机时的负简特性曲线 [负荷特性为P=0.75+0.252G(G=lw) 初始运矿点时电和功水均等于1】 。高比例电阻负荷 图2-14给出了含75%恒电阻时的负荷特性曲线(系统特性曲线保持不变)。此时负荷 功率方程为P=0.25+0.75n2G2,对应于曲线a与b的G值均取为1.0u,对应于曲线c 的G值取为1.2u,且认为曲线c中G值的增加来自恒温负荷的调整特性,即表示全部加 热器都投人运行。L心℃动作和恒温调节会导纹负荷增加,但增加后的负荷功率不超过初始 值1.0pu(图中的垂直线)。 当发电机电流未越限时,扰动后运行点为垂直线与系统扰动后特性曲线的交点,表示 负荷全部恢复,此时变压器变比大约为1.03。假设发电机电流越限但负荷电导尚未增加, 运行点为曲线b与考虑发电机电流限制时的系统特性曲线的交点。当考虑负荷电导增加 时,运行点相应为A点。 显然,这种负荷特性曲线比较理想,系统不容易因失去运行点(对应于负荷与系统特 性曲线无交点)而导致发生电压崩微,且有可能稳定运行在电压很低的情况,对应于P- 25 V曲线的下半支。在实际系统中,最终状态将依赖于电动机行为(包括堵转或脱网)、继 电保护动作和自动或手动调节的恒能负尚大小。如果系统运行点在P-V曲线的下半支, 则此时增加负荷电导将导致负荷实际吸收功半减少。正如附录F所述,在发生局部电压崩 稳 遗期间,电力系统确实可以稳定运行在极低的电压水平下(图下)。 曲线b与考意发电机电流越限时系统特性曲线的拐点相交。此时增大变压器变比反而 第6章将叙述这种情况。功率实际上是电动机的内部特性,还应当考虑电机本身的阻抗
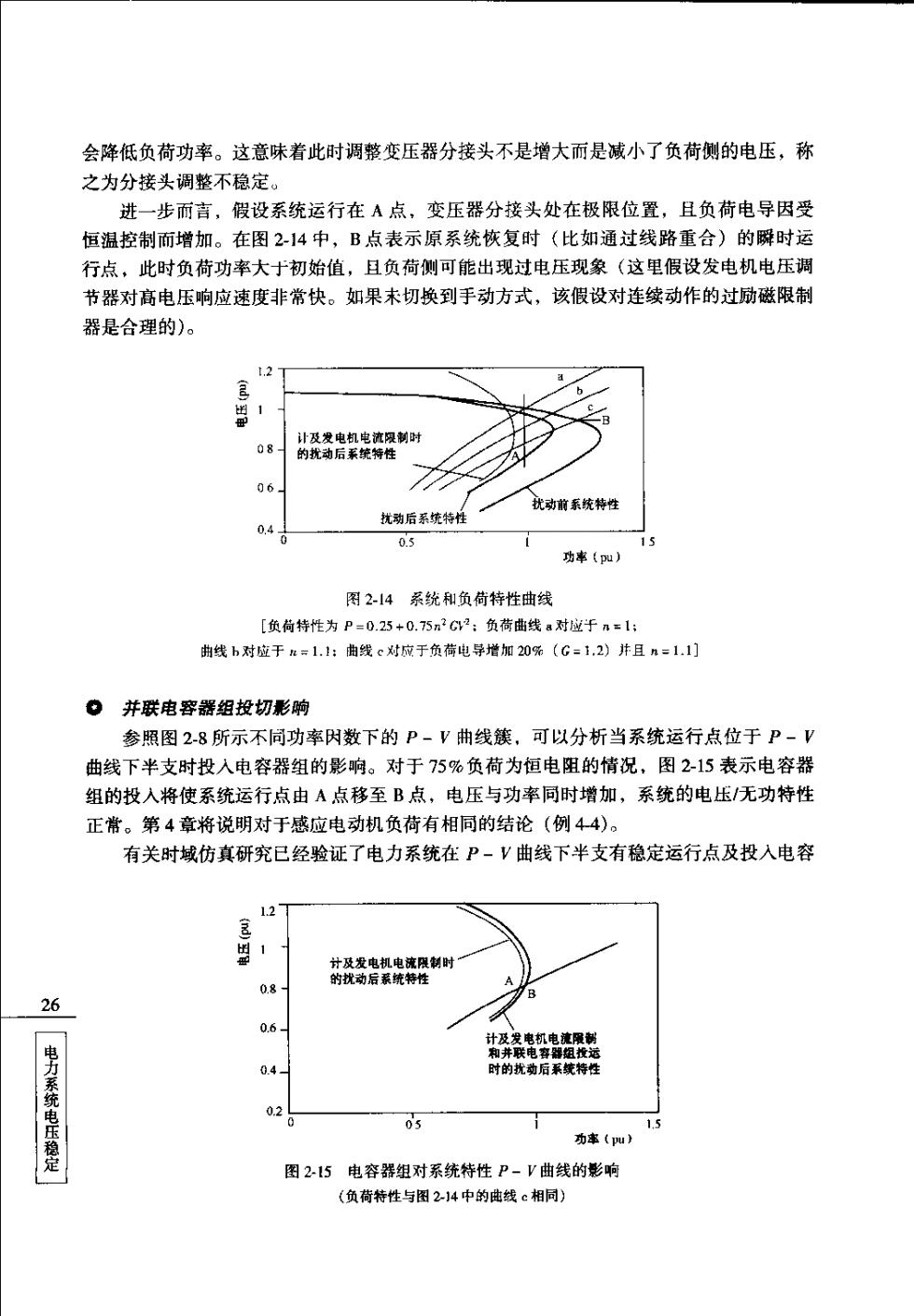
会降低负荷功率。这意味着此时调整变压器分接头不是增大而是减小了负荷侧的电压,称 之为分接头调整不稳定。 进一步而言,假设系统运行在A点,变压器分接头处在极限位置,且负荷电导因受 恒温控制而增加。在图2-14中,B点表示原系统恢复时(比如通过线路重合)的瞬时运 行点,此时负荷功率大于初始值,且负荷侧可能出现过电压现象(这里假设发电机电压调 节器对高电压响应速度非常快。如果未切换到手动方式,该假设对连续动作的过励磁限制 器是合理的)。 2 08 的瓷器轻隆林保制叶 06 犹动前系统特性 04 功率《四 图2-4系统和负荷特性曲 [负荷特惟为P025+0.75m2G2:负荷曲线。对位于n=1: 曲线b对应于:=1.:曲线c对疯于负荷电茅增加20%(G=1,2)并且n=1.] 。并联电容器组投切影响 参照图2-8所示不同功率内数下的P-V曲线熊,可以分析当系统运行点位于P-V 曲线下半支时投入电容器组的影响。对于75%负荷为恒电阻的情况,图2-15表示电容器 组的投入将使系统运行点由A点移至B点,电压与功率同时增加,系统的电压/无功特性 正常。第4章将说明对于感应电动机负荷有相同的结论(例44)。 有关时域仿真研究已经验证了电力系统在P-V曲线下半支有稳定运行点及投入电容 12 08 26 06 及发电机电速制 0.4 时的扰动后莱统特性 乘统电压稳定 05 功车(则 图215电容器组对系统待性P-V曲线的影响 (负荷特性与图214中的曲线c相同)