
2 电压稳定性概念 本章将介绍电压稳定,即本书的主题。首先给出电压稳定性的有关定义,说明电压失 稳机理及其与功角稳定性的关系;然后讨论饱和电力系统(mature power systems)发生电 压稳定性问题的原因;最后介绍应用P-V曲线和V-Q曲线分析电压稳定性的静态方 2.1电压稳定、电压崩溃与电压安全 电压稳定性涉及电力系统中发生的众多现象。鉴于这种情况,电压稳定性对不同的】 程师而言表示不同的含义。例如当考虑感应电动机、空调负荷或HVDC联线特性时,电压 稳定性属于快变化范酶;而如考虑由变压器分接头的机械动作引起的电压稳定性,则它又 属于慢变化范畴。为此,工程师们及研究人员曾经讨论过合适的电压稳定性分析方法,并 且在电压稳定性是静态现象还是动态现象这一问题上持有不同的观点。 对大多数工程师而言,他们经常交替使用电压失稳和电压崩遗两个术语。 电压稳定或电压崩溃一般被看作电力系统的稳态“承受能力”问题,可以采用静态 (如潮流)分析方法,并把电力系统稳态运行状况下从电源端到负荷端的无功传输能力作 为电压稳定性的主要方面。为此,1987年图际大电网会议(CGE)专题报告推荐了基 于稳态数学模型的电压稳定分析和电力系统规划方法, 然而,网络最大功率传输能力并非电压稳定极限。 电压失稳或电压崩费是一个动态过程。“稳定”一问本身意味者是一个动态系统,而 电力系统正是一个动态系统。相对于功角(同步)稳定,系统电压稳定的动态特性主要决 定于负荷与电压控制措施。电压稳定已经被称为负荷稳定。 2 。定义 电压稳定性是电力系统所有稳定问题中的一个子集,这里采用CIGRE报告]中提出 电力系统电压稳定 的定义。这些定义是根据文献[4]并考虑到文献[5~7]的观点提出的,它们同其他动态系 统的稳定问题定义相类似,具休如下: 电力系统在给定的稳态运行点道受任意小的扰动后,如果负荷节点的电压与扰动 前的电压值相同或者相近,则称系统在给定运行点为小干扰电压稳定(小干扰电压稳 定对应于线性化动态方程所有祷征值的实部为负。为便于分析,描述变压器分接头动

作特性的离散模型需用连续等值模型代替)。 电力系统在给定的稳态运行点通受一定的扰动后,如果负荷节点的电压能够达到 扰动后平衡点的电压使,则称系统为电压稳定。此时,系统扰动后的状态住于系统扰 动后稳定平衡点的吸引战之内0。 电力系统在给定的稳态运行点通受一定的扰动后,如果故倖后平衡点超出系统运 行限制范围,系统将发生电压崩溃。电压崩溃可能是全局性的(停电)也可能是局部 范国的。 电压失稳即为失去电压稳定,其后果是电压持续下降(或上升)。导致系统不稳定的 控制元件达到极限(如变压器分接头达到极限位置、温控负荷达到最大值等。 一译者 注)或者采取其他控制(例如断开负荷)都有助于电力系统重新建立稳定运行点 电压稳定通常涉及到大扰动(包括负荷或功率传输快速增长),而且电压失稳几乎都 表现为电压非周期性单调下降。此外,电力系统也可能发生振满性电压失稳,但不包括 控制失稳。电力系统是可能发生控制失稳的、比如静止无功补偿器的增益过高,或者控制 并联电容器组的电压继电器死区太小。过电压现象和诸如发电机自励磁不稳定不在上述定 义的范围内。过电压通常只是涉及-一个装置本身的问题而非电力系统的稳定问题。 电压安全这个术语也被广泛采用。它是指电力系统的一种能力,即不仅在当前运行条 件下电压稳定,而且在可能发生的预想事故或负荷增加情况下仍能保持电压稳定。它意 味着相对于可信的预想事故集合,电力系统当前运行点距离电压失稳点(或者最大功率传 输点)具有足够的安全裕度。 虽然电压稳定性问题涉及到电力系统的动态特性,但在对系统的电压稳定性问题进行 快速近似分析时,基于潮流计算的静态分析方法通常是有用的。 2.2电压失稳的时域与机理 电压失稳和电压崩遗的动态过程历时从小于13到数十分钟,应用时间响应图可以描 述电力系统的动态现象,。图21表示出影响电压稳定性的多种系统元件和控制装置。 然而由图可知,对于系统发生的特定事件或情景,只有某些元件和控制起作用。系统特性 和扰动类型将决定系统发生现象的性质。 图2」将电压稳定根据历时长短划分为暂态和长期两种,这两种时域过程基本上总可 13 以严格区别。附录F为按时域特性划分的世界电力系统实际发生的电压稳定事例。 。机理一情 这里将通过3种系统情描述两类电压失稳的基本概念。 (1)情景1:暂态电压稳定。暂态电压稳定的时城范围小于10,这段时间自然也是 性概 0下节将介绍平衡点及其吸引城
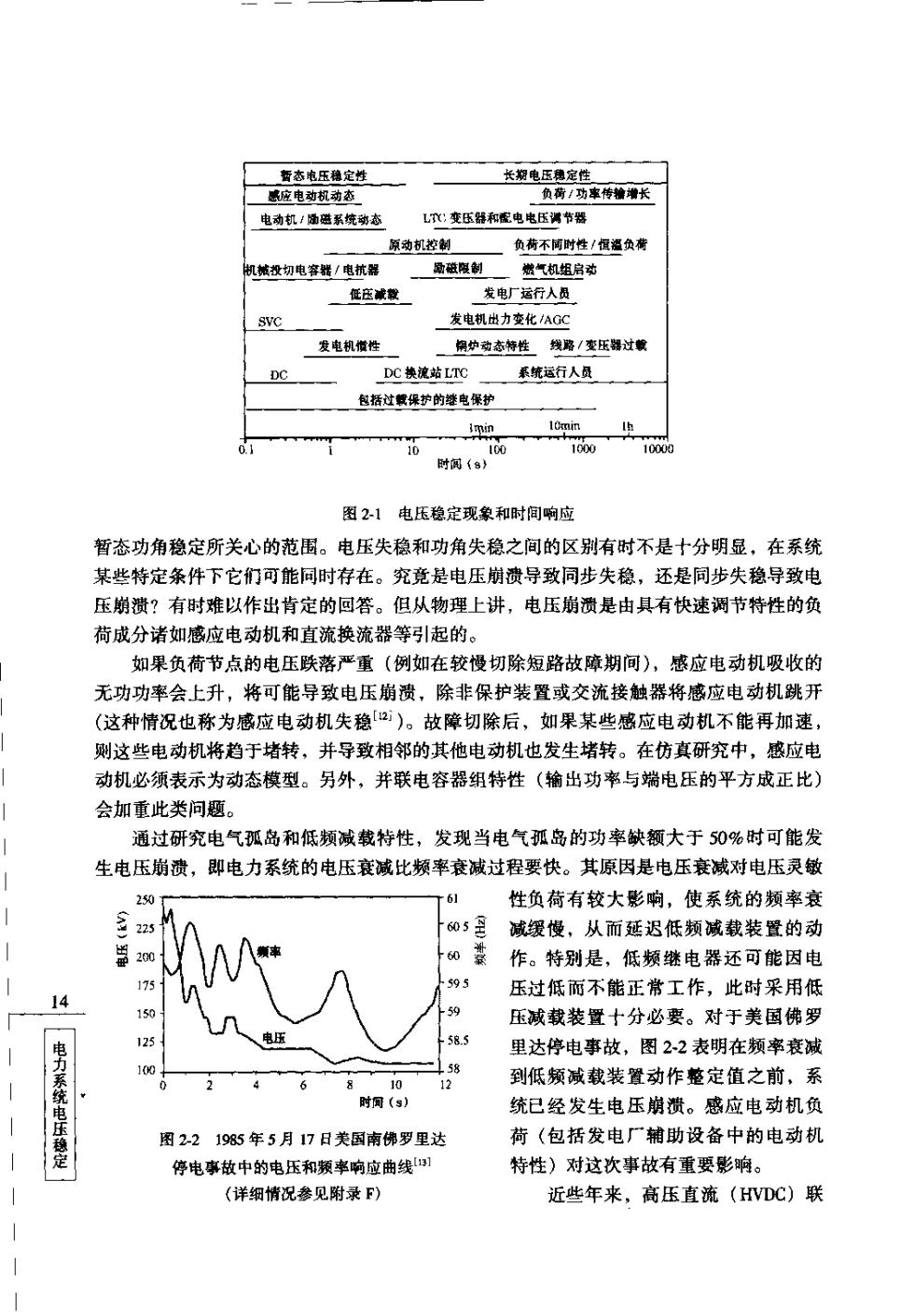
斯衣电压定性一 电动机/通系统态 :变压和电电区节 原动机控制 负荷不阿时性/恒道负衡 机城投切电容继/电抗器 觉破限制嫩气机组启动 任在诚整 发电厂运行人员 SVC 发电机出力变化AC 发电机微性 响炉劳态特性线路/变压海过鞭 DC换浪站LTG 系统运行人员 越搭过收保护的整电条护 16001000 图2.1电压稳定现象和时间啊应 暂态功角稳定所关心的范围。电压失稳和功角失稳之间的区别有时不是十分明显,在系统 某些特定条件下它们可能同时存在。究竟是电压崩遗导致同步失稳,还是同步失稳导致电 压崩渍?有时难以作出肯定的回答。但从物理上讲,电压崩渍是由具有快速调节特性的负 荷成分诸如感应电动机和直流换流器等引起的。 如果负荷节点的电压跃落严重(例如在较慢切除短路故障期间),感应电动机吸收的 无功功率会上升,将可能导致电压崩遗,除非保护装置或交流接触器将感应电动机跳开 (这种情况也称为感应电动机失稳)。故障切除后,如果某些感应电动机不能再加速, 则这些电动机将趋于堵转,并导致相邻的其他电动机也发生堵转。在仿真研究中,感应电 动机必须表示为动态模型。另外,并联电容器组特性(输出功率与端电压的平方成正比) 会加重此类问题。 通过研究电气孤岛和低频减载特性,发现当电气孤岛的功率缺额大于50%时可能发 生电压崩遗,即电力系统的电压衰诚比频率衰减过程要快。其原因是电压衰减对电压灵敏 61 性负荷有较大影响,使系统的频率衰 605 减缓慢、从而延迟低频诚载装置的动 200 0 作。特别是,低频继电器还可能因电 175 9 压过低而不能正常工作,此时采用低 压减载装置十分必要。对于美国佛罗 电压 583 里达停电李故,图2-2表明在频率衰诚 46 8 ( 到低频减载装置动作整定值之前,系 统已经发生电压期溃。感应电动机负 图2-21985年5月17日美图南佛罗里出 荷(包括发电厂辅助设备中的电动机 定 停电事故中的电压和频率响应曲线 特性)对这次事故有重要影响。 (详细情况参见附录F) 近些年来,高压直流(HVDC)联

线接入弱系统引起了暂态电压稳定问题。例如,仿真结果表明美国加州南部地区电网 在重裁条件下普受大扰动时易发生电压雠费,而目位于路衫附近的两个大型逆变站对系 统电压崩费过程有加速作用。对此,有时(以同步功率为代价)需要通过降低直流线输送 功率(从而也减少了逆变站的无功需求)来保持系统电压稳定。第8章介绍了包含VDC 联线的系统电压稳定性问题。 (2)情景2:长期电压稳定。长期电压稳定历时范围为数分钟,典型情况为2-3min。 在此期间,运行人员通常不可能进行干预。“中期”电压稳定、“暂态后”电压稳定或“扰 动后”电压稳定等术语也用于描述此类问题。 发生长期电压失稳事故时电力系统一般处于高负荷水平,且从远方电源送人大量功 率,并伴随突然出现的大扰动。由于负荷的电压灵敏性,电力系统暂时能够保持稳定。但 扰动(如负荷区域失去大容量发电机或系统失去主要输电线路)会引起无功损耗增加以及 负荷区域电压下降。这时,输电线路上的℃0变压器和配电网中的电压調节装置会相 继动作,恢复配电网电压水平,结果相应恢复了负荷功率 负荷功率的恢复会进一步加剧输电线路电压的下降。附近的发电机将处于过励磁与过 载状态,而当机组的过励磁能力到达设定运行时间(一般为1~2m)时,过励磁限制器 (或发电厂运行人员)会将励磁电流减小到额定值,使得远方发电机必须提供所需的无功 功率。正如在第1章中所讲,由远方发电机向负荷区域提供无功是低效率和无效果的做 法,致使发电和输电系统不能够再支攀负荷无功需求和系统无功损耗,随即系统电压迅速 下降,发生局部或全局性的电压崩遗。最后阶段包括感应电动机堵转和继电保护装置动 作。根据负荷类型的不同(包括低压解列措施),系统电压崩费可能是局部或全局的。 (3)情景3:长期电压失稳。这类长期电压失稳过程经历的时间更长,由负荷大量增 加(比如早晨或下午的负荷增长)或传输功率大量增长导致。负荷增加的速度用MW/min 表示,通常比较快。此时为避免系统发生电压失稳,运行人员需要及时投入无功补偿装置 或者进行切负荷。另外篇要考虑的重要因素有:输电线路过载限制(数十分钟),以及负 荷因低电压而失去不同时性(由于系统存在恒能负荷和恒温控制的负荷)。失稳的最后阶 段涉及情景(1)和(2)所叙述具有快速响应特性的装置的动作。 电力系统的各种元件在不同时域内存在许多相互作用(如图2-1所示)。例如,利用 分接头调整电压可以防止由于恒能负荷的恒温调节而破坏负荷工作的不同时性:又如,过 励磁限制器动作会影响发电机正常的电压调节功能。 15 机理—负荷动态,平衡点和吸引域 电压稳定已被称为负荷稳定。这里的“负荷”是指从输电线路高压母线向负荷侧看进 ing),ULTC (Unde 电压稳定性 d Tap Chan 。如果读者认为本小节内容太,可以智时过。待阅读完本康其余肉容和第4率后再进行。参考文献[5 [6】和151对此有进

去的全体,包括次输电系统和配电系统的影响。负荷功率随电压降低而暂时减小而后又逐 渐增加的特性称为负荷的恢复特性,其对电力系统电压稳定性有着重要影响。 有功负荷恢复特性的机理包括以下3种情况: (1)感应电动机在端电压突然降低数秒钟内快速响应,其有功负荷最终与机械负载相 匹配。由于电动机存在惯性,转差不可能突变,因此根据熟悉的等值电路可知:在电源电 压突然降低时感应电动机表现为阻抗特性。而对于电压缓慢降低情况,响应快速的感应电 动机能够跟随系统其他装置的慢动态过程,表现为恒定有功特性。 (2)大功率供电变压器及配电电压调节器的分接头在数十秒至数分钟内进行自动调 节,结果恢复了负荷侧的电压,从而恢复了对电压变化反应灵敏的负荷的有功功率,并且 相应恢复了无功负荷及并联补偿装置的无功输出。 (3)恒能电阻性负荷在温度调节装置或人工控制下恢复工作。从集结负荷角度看,电 压降低将破坏负荷在随后时间段内的不同时性。 作为初步近似,3种负荷恢复机理的动态特性可用一阶动态模型表示,只含有一个 时间常数(对于变压器分接头,考虑到存在死区、电压继电器和定时继电器,并且动作 具有离散特性,这种近似相当粗略)。虽然各自的时间常数不同,但方程式的形式相 同。因此从定性分析而言,负荷恢复的机理是统一的刀。大功率供电负荷母线上可能 存在这3种类型的负荷,如图23所示。 PO 载售测压的分 感应电对西⊙ 其他负 开急0 图2-3电压灵鼓性负荷恢复的3种机理口 描述3种负荷恢复机理的一阶动态模型的状态变量可以分别选取电动机转差()、变 压器变比()和负荷电导(G)。当每种状态变量由零逐渐增加时,负荷功率先是随之增 加并达到最大值,而后逐渐下降(如图24所示)。在状态变量增加过程中,电压单调下 降。 对感应电动机而言,图24所示曲线同熟悉的转矩一转差特性曲线相似,可用一阶微 16 P 分方程式表示为 找动前曲峻 初始与最终功率 2d=P。-P. (2.1) 式中P。—初始机械功率。为简单起见,假设 扰勒后的最好曲线 其为常数。 在大干优后系统要保持稳定,对应于系统达 定 国24负荷功率与动态模型中的状态变量到最终结构(即故摩切除后)时刻的转差必须在 (摘自Van Catsem的文献[7]) 故后系统稳定平衡点x的“吸引域”之内