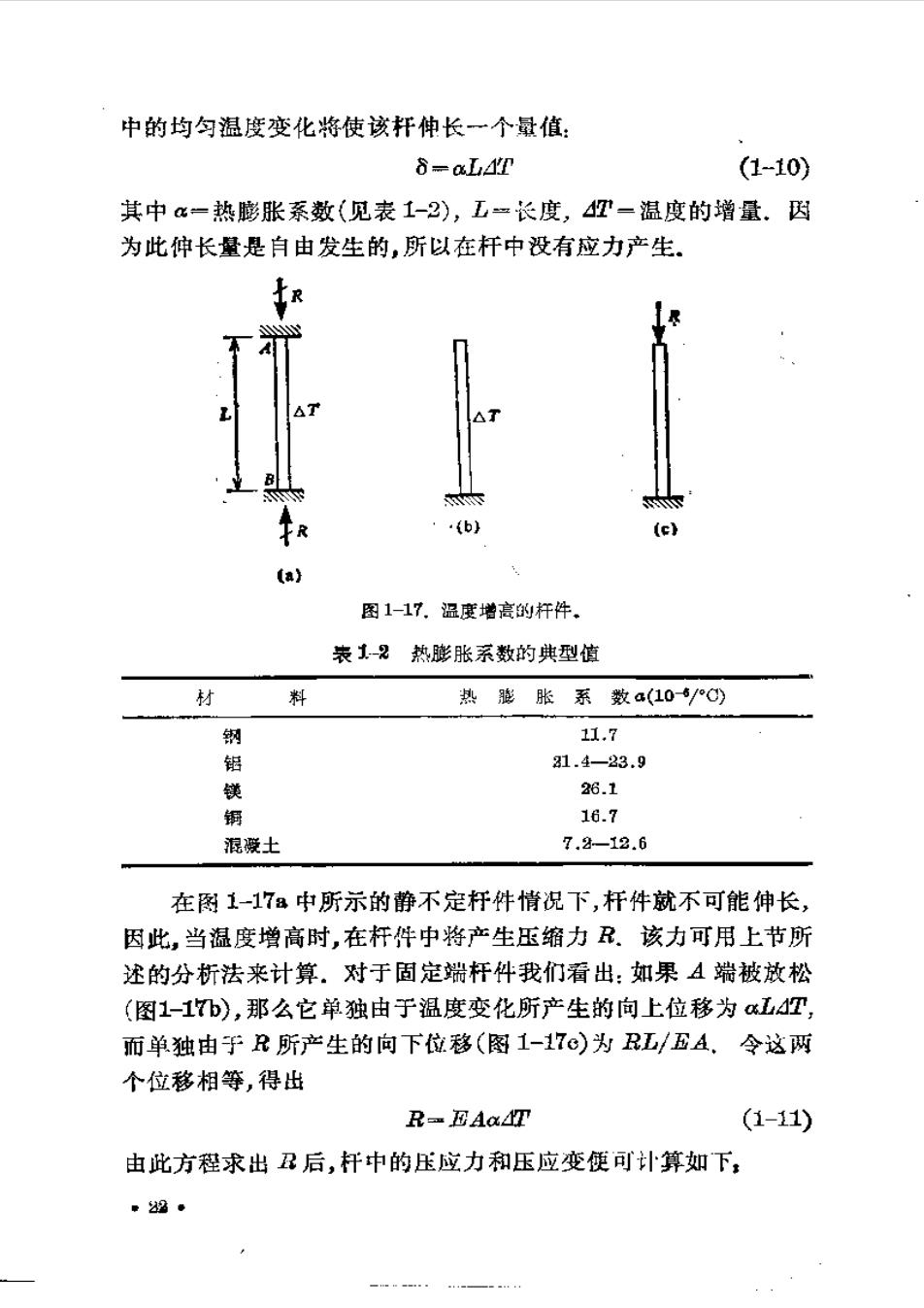
中的均匀温度变化将使该杆伸长一个量值: 8=L4虹 (1-10) 其中“一热膨胀系数(见表1-2),工一长度,埋=温度的增量.因 为此伸长量是自由发生的,所以在杆中没有应力产生 AT △1 {b) a】 图1-17.温度增度的杆件. 表1-2热,膨胀系数的典型值 材 料 热膨胀系数a(10/C) 钢 11.7 铝 1.4-23.9 镁 26.1 铜 16.7 混潑土 7.2-12.6 在图1-17a中所示的静不定杆件情况下,杆件就不可能伸长, 因此,当福度增高时,在杆件中将产生压缩力R.该力可用上节所 述的分析法来计算。对于固定端杆件我们看出:如果A端被放松 (图1-1b),那么它单独由于温度变化所产生的向上位移为江悝, 而单独由于R所产生的向下位移(图1-17o)为R工/BA.令这两 个位移相等,得出 R=EAq4T (1-11) 由此方程求出丑后,杆中的压应力和压应变便可计算如下: 单29●
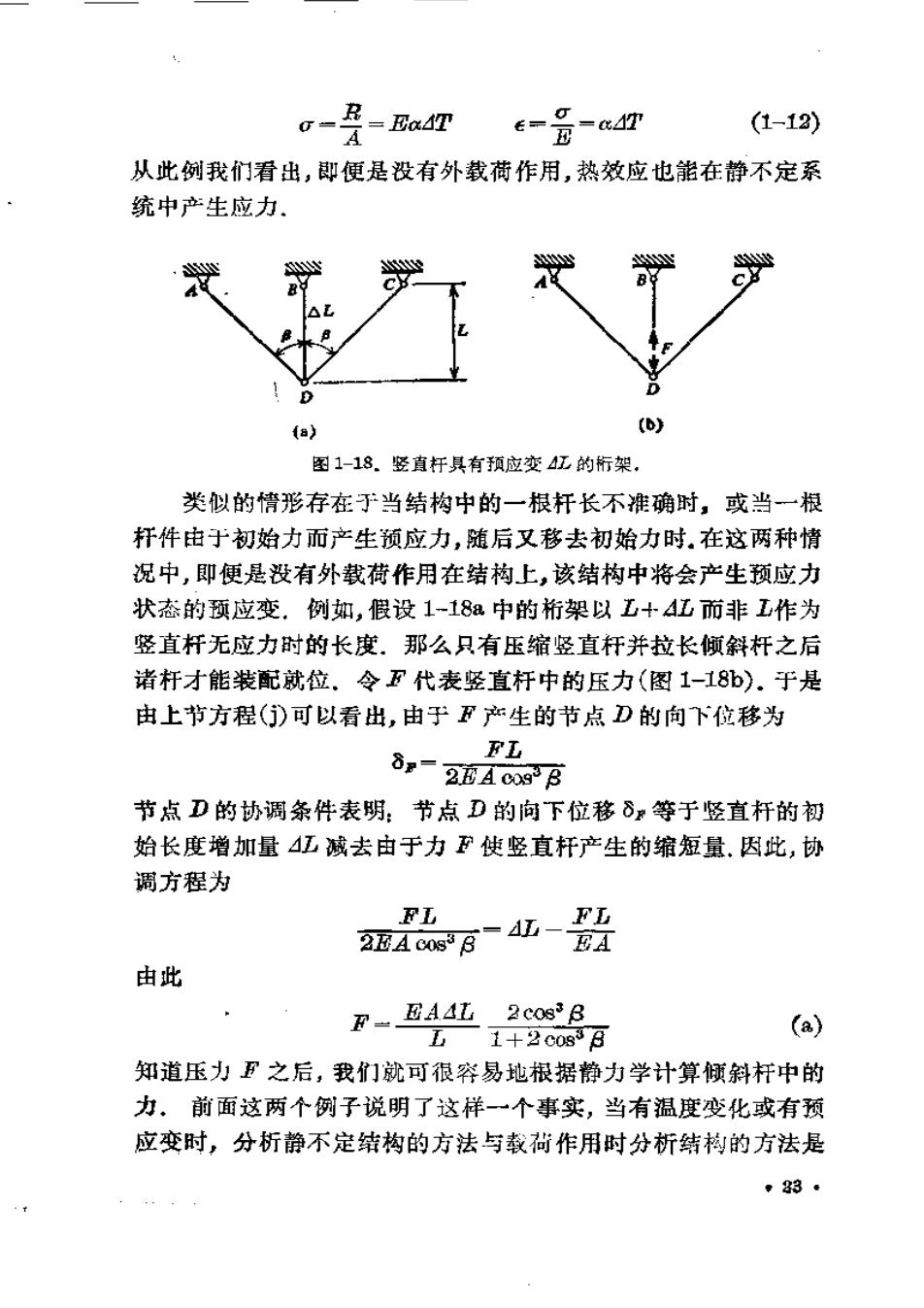
=EaAT (1-12) 从此例我们看出,即便是没有外载荷作用,热效应也能在静不定系 统中产生应力, 力 (a) (D) 图1-18.竖直杆具有预应变江的桁架, 类似的情形存在丁于当结构中的一根杆长不推确时,或当一根 杆件由于初始力而产生预应力,随后又移去初始力时.在这两种情 况中,即便是没有外载荷作用在结构上,该结构中将会产生预应力 状态的预应变.例如,假设1-18a中的桁架以工+4工而非工作为 竖直杆无应力时的长度.那么只有压缩竖直杆并拉长倾斜杆之后 诸杆才能装配就位.令F代表竖直杆中的压力(图1-18b).于是 由上节方程()可以看出,由于F产生的节点D的向下位移为 8罗一 FL 2.4 cog B 节点D的协调条件表明:节点D的向下位移δ:等于竖直杆的初 始长度增加量4工减去由于力F使竖直杆产生的缩短量.因此,协 调方程为 FL FL 2A c0s38 EA 由此 丑一EA4比 2cos3 B L 1+2 (a) 知道压力F之后,我们就可很容易地根据静力学计算倾斜杆中的 力,前面这两个例子说明了这样一个事实,当有温度变化或有预 应变时,分析静不定结构的方法与载荷作用时分析结构的方法是 ,83·

相同的。 作为最后的一个例子,让我们再次研究图1-18:所示的桁架, 并设竖直杆受热使温度升高悝.只要我们使红等子当该杆为 自由伸展时所发生的温度膨胀,则温开对杆力产生的效应就与竖 直杆具有初始伸长缸时的效应相同.因此,为了得出竖直杆中 由于温度变化所产生的力F,我们只斋在方程(a)中用x工T代督 4红即可. 1.8 非线性性态 在以前的讨论中总是假设结构的材料服从虎克定律。现在让 我们讨论当应力超过比例极限时绩构拉伸和压缩的性态。我们将 假设材料的应力-应变图为已知. 如果结构是静定的,其轴力可用静力学求出而不需要考虑材 料的性质,知道诸力之后,我们便可计算结构每点处的应力.最后, 我们使用应力-应变图就可得出每点的应变,从而也可以得到每 一杆件长度的变化及所产生的位移.这种分析静定系统的步豫是 十分简单明了的,并将在本章末尾习题1.8-1至1.85中说明. F2 (a) b)」 (c) 图1-0,具有非线性应力-应变图的静不定桁架。 在静不定系统中,分析变得复杂多了,因为不首先求出位移, 力就不可能求出,而位移本身义取决于力和应力一应变的关系.在 这样的一个系统中可以采用此凑法或逐次渐近法.为了说明此种 分析的方法,让我们再次考虑图1-19a所示的对称三杆桁架,只是 L24

现在我们将认为桁架的材料有图1-19h所示的应力-应变图.我们 从假设节点D处竖直立移δ的试武算值开始分析,然后,根据节点 D的维利奥特图,可以得到所有三根杆的相应伸长量.这种计算方 法保证了节点处的协调条件是满足的.其次节点处力的平衡必须 予以校核.杆中应变可由伸长量求出,然后应力可由应力一应变图 求出.知道了各杆的应力,我们就可以求出杆中的力,并校核节点 D处的平衡。如果最初假设的6正确无误,我们就会发现节点D 处诸力的平衡将被满足。否则,我们会发现诸力并不处于平衡,因 此,必须选择新的8试算值,并重复这一计算过程。最后,我门将 得到能使节点D处的协调和平衡都得以满足的8值.各杆中相 应的力将是正确的, 另一种步骤是从假设竖直杆中力F2的试算值开始.然后,使 用节点D处诸力的平衡,我们便可计算出斜杆中的力.接着,每 根杆中的应力就能确定,然后确定应变(根据应力-应变图)以及伸 长量。最后,我们根据节点D处的维利奥特图可以确定所有三根 杆的伸长量是否彼此协调.如果它们是协调的,那么F的试算值 就是正确的,此分析就完成了.否则,必须选择新的F试算值,并 重复这一过程,直到平衡和协调均得到满足为止, 根据以上所述的方法来分析图1-19a所示的静不定桁架,对 于任一个所假设的载荷P值,我们可以得出桁架的变位和各杆的 力.因此就可能得到载荷从零增到其最大值时桁架性态的全貌 塑性分析 有少数材料,尤其是结构钢,在线性弹性区段之 后有一个显著的屈服区段,这种材料的应力一应变图可以用两根直 线相当精确地加以理想化,如图1-19o所示.假设该材料直到屈 服点之前服从虎克定律,此后它在常应力条件下屈服,屈服点处的 应力和应变分别用σ:和,来表示.屈服而应力并不增加的材料 称为完全塑性的.当然,因为应变硬化的缘故,钢的应力一应变图 最终上升到屈服应力之上,如同早已在第1.3节中解释的那样,但 是,此现象发生之前,变形已经很大,而结构失去了它的作用,因 此,根据图1-19c所示的图形为基础来分析处于塑性范围内的钢 ·25·

结构,已成为通用的作法.对于钢来说,此同一图形既可用于受拉 也可用于受压.具有图1一190所示的应力-应变图(亦即在线性弹 性区段之后有完全塑性区段的材料)称为弹一塑性材料.采用这 些假定所作的分析称为结构的塑性分析或极限分析、 塑性分析的方法可用例题加以说明,再次研究图1-19a中的 三杆桁架,并假设诸杆均由弹-塑性材料所制成(图1-19o).当载 荷逐渐增加时,杆中的力也将增大,只要应力低于屈服应力σ, 此力就可用弹性分析确定(见第1.6节的例题1).如果诸杆的横 截面面积相等,最终,比外侧杆的力要大的中间杆将达到屈服应力 ¤.这种情祝出现在F9等于心A时,A为每根杆的横截面面积. 当载荷P进一步增加时,斜杆中的力也要增加,但力卫保持常 数,因为中间杆已成为塑性的了、最后,外侧杆也将变成塑性的, 于是结构就不能再承受附加的载荷.所有杆子实际上将在常值(最 大)的载荷下继续伸长.这一载荷称为极限载荷P. 上段所述的现象用图1-19a所示桁架的载荷-变位图描绘在 图120中.载荷P取为图的纵坐标,而节点D的变位δ为横坐 标。从原点O至点A,所有三根杆均为弹性,而杆力(根据第1.6 节例题1)为 P cos8 P F1=1+3co8B 1+2c09%B 中间杆的屈服从点A开始,其相应的载荷称为屈服载荷卫,令上 式中F等于y,得出: Py=Ov4(14200938) 从A到B.中间杆的力,保持不变,等于σA,而斜杆中的力可根 据节点D的平衡求得(见1.6节的方程): P1i P-OA 2c08B 在B点处,斜杆也屈服了,因此,F1一σA,根据节点D的平衡,我 们得到极限载荷P4下述结果: P=4(1+2C08B) ·26● 一