
- E48+4。=P (g) 此式得出 B.-Pab EA五 (h) 知道δ。后,现在我们可从方程(⊙)求出,和: 自然,这些结果与前面求出的完全相同. 归纳起来,第二种分析方法从选取适当的位移作为未知量着 手。该位移必须按这样的方式来选择,即结构各个部分的力都可 用它来表达.然后将这些力纳入平衡方程(方程).代入用位移 所表示的力的表达式(方程g)之后,我们即可解出未知的位移(方 程h).最后,根据位移便可求得诸力. 这一分析方法称为位移法或刚度法.前一命名是由于以位移 作为未知量的缘故,后一命名起缘于平衡方程(方程g)中的系数 (A/a和A/)均为刚度、此法也是一个很通用的方法,它可 用来分析多种类型的结构, 对于大型结构,在力法和位移法之间的抉择取决于许多因素, 例如结构的几何形状和节点数目.然而在本节中我们仅考虑这两 种方法几乎都同样适宜的问题,因此,在这两种方法之间的抉择带 有若干任意性。以后在第七章和第十一章我们还将进行静不定结 构的分析. 例题1 作为第个例子,让我们用力法分析图1-13a中的平面桁架。 假设该桁架是对称的,我们看出外侧两杆的拉力是相等的,则根据诸力在竖 直方向的平衡,我们得出 ·从历史的观点来看,欧拉于1744年成为第一位分析静不定系统的学者,他考患 了一个支承在弹性基础上有四条限的刚性桌子的问题(参考文献11)。下一步工作 是由纳维尔(Navier)进行的,他于1825年指出静不定反力可借计入结构的弹性来求 得(参考文献1-14),纳维尔求解了…个与图1-14所示桁架相类似的桁架. •17
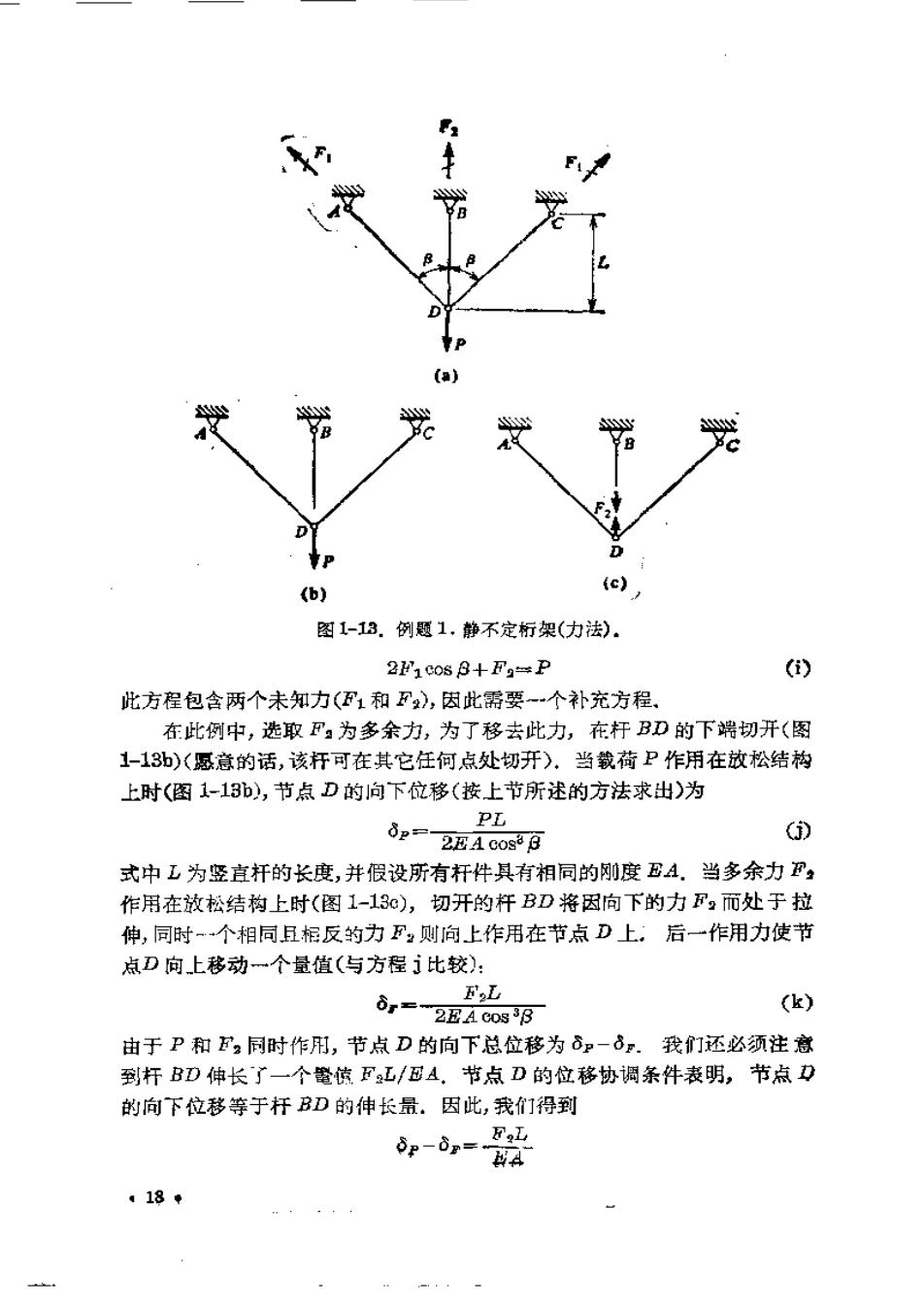
D c (b) 图1-13.例题1.静不定析架(力法). 211cos 8+F2=P (i) 此方程包含两个未知力(1和),因此需要-个补充方程、 在此例中,选取F,为多余力,为了移去此力,在杆BD的下端切开(图 1-13b)(愿意的话,该杆可在其它任何点处切开).当载荷P作用在放松结构 上时(图1-13),节点D的向下位移(按上节所述的方法求出)为 PL p--2A cosB () 式中工为竖直杆的长度,并假设所有杆件具有相同的刚度EA.当多余力P, 作用在放松结构上时(图1-13c),切开的杆BD将因向下的力F,而处于拉 伸,同时个相同且相反的力F:则向上作用在节点D上:后一作用力使节 点D向上移动一个量值(与方程比较): F2L δr=2z4cos3 (k) 由于P和F2同时作用,节点D的向下总位移为δp一8.我们还必须注意 到杆BD伸长了一个鳘镇F工/EA,节点D的位移协调条件表明,节点卫 的向下位移等于杆BD的伸长最。因此,我们得到 4-=路 、18
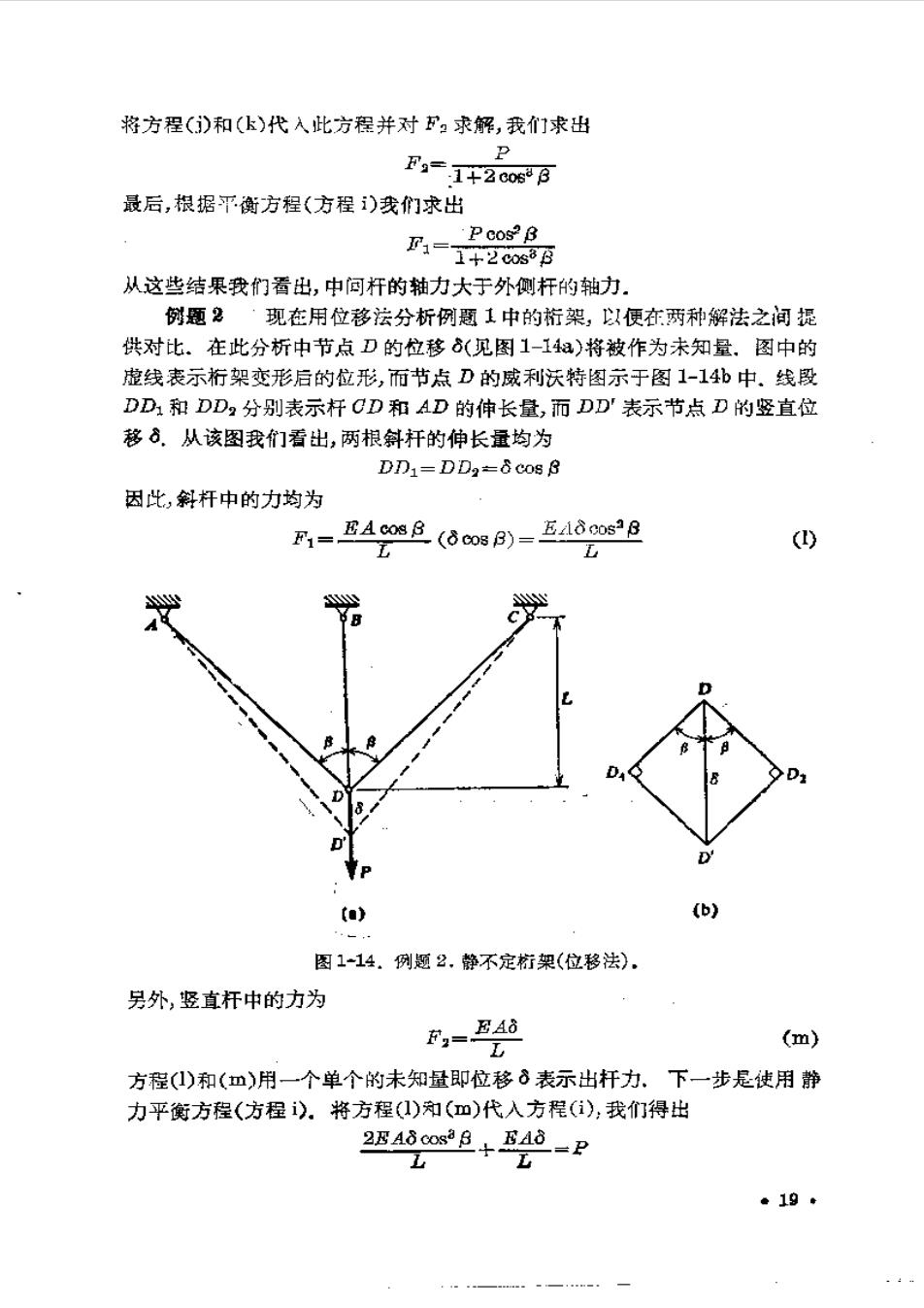
将方程()和(k)代入此方程并对F妇求解,我们求出 P F=1+2c0s°8 最后,根据平衡方程(方程)我们求出 A=88 从这些结果我们看出,中问杆的轴力大于外侧杆的轴力. 例题2·现在用位移法分析例题1中的桁架,以便在两种解法之间提 供对比.在此分析中节点卫的位移6(见图1-1a)将被作为未知量.图中的 虚线表示桁架变形后的位形,而节点D的威利沃特图示于图1-14b中.线段 DD和DD,分别表示杆CD和AD的伸长量,而DD'表示节点D的竖直位 移6.从该图我们看出,两根斜杆的伸长量均为 DD1=DD2=6 cos 8 因此,斜杆中的力均为 -A cos B (00 B)-E600s18 () (a) (b) 图114.例题2.静不定粉架(位移法). 另外,竖直杆中的力为 -0 (m) 方程()和(m)用一个单个的未知量即位移8表示出杆力、下一步是使用静 力平衡方程(方程》.将方程(1)(m)代入方程(),我们得出 246 cos38 46 2P 。19+
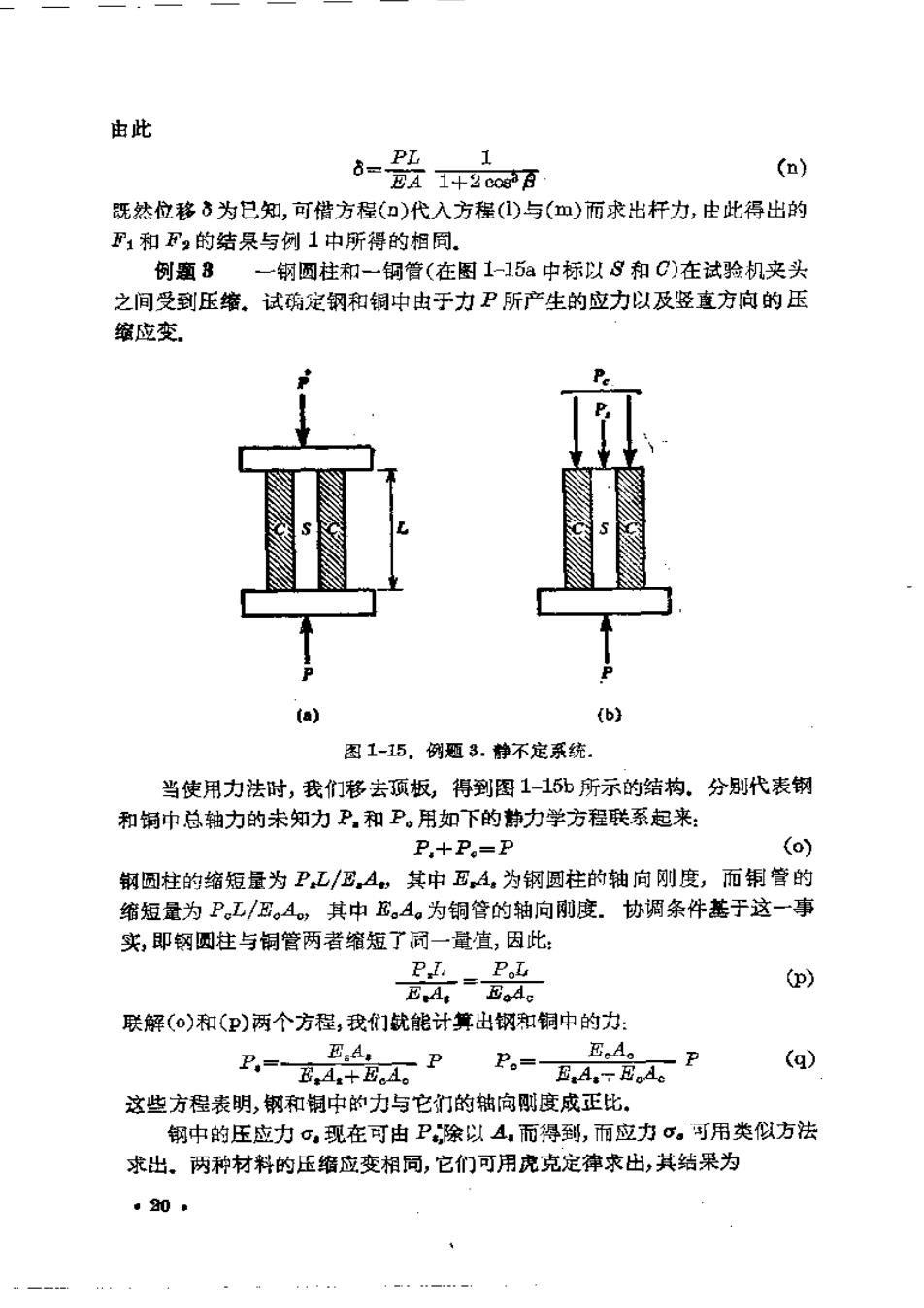
由此 d= EA1+2e0g3百 (n) 既然位移6为已知,可借方程(知)代入方程()与(血)而求出杆力,由此得出的 F1和F2的结果与例1中所得的相同. 例题8 一钢圆柱和一铜管(在图1-15a中标以8和C)在试验机夹头 之间受到压缩。试确定钢和铜中由于力P所产生的应力以及竖直方向的压 缩应变 (a) (b) 图1-15,例题3.静不定系统, 当使用力法时,我们移去顶板,得到图1-15所示的结构.。分别代表钢 和铜中总轴力的未知力P,和P。用如下的静力学方程联系起来: P+P。=P (o) 钢圆柱的缩短量为P工/EA,其中EA。为钢圆柱的轴向刚度,而铜管的 缩短量为P工/E。A,其中。A。为铜管的轴向刚度.协调条件基于这一事 实,即钢圆柱与铜管两者缩短了同一量直,因此 PI PoL (p) EA。E。A。 联解(o)和(P)两个方程,我们就能计算出钢和铜中的力: EAr P=EA十Ed。P B。A。 P。=,4,8 (q) 这些方程表明,钢和铜中的力与它们的轴向刚度成正比, 钢中的压应力σ,现在可由P除以4,而得到,而应力σ。可用类似方法 求出。两种材料的压缩应变相同,它们可用虎克定律求出,其结果为 ·2a0●

P 6=·巴,A,+B (r) 此方程表明应变等于总的载荷除以钢零件和铜零件的轴向刚度之和。 例题4 用位移法求解上面例题。 在此例中的未知位移为两端极的相对位移ò,它与钢零件和前零件的缩 短量是相同的。当用位移8袤达时,力P。和P。为 丑,=B4d 工 P。=E。4d (8) 将这些表达式代入平衡方程,得 E,A0+EAd=卫 由此我们求得位移6, 8=- PL EA。+。A。 现在,将这一8的表达式代入方程(),给出力 P,和P。.这些结果与例3所得结果一致(见 方程q),另外用工去除δ给出与方程()一 致的应变e. 比较例题3和例题4表明,尽管力法和位 移法在观点上基本不同,但在某些榜况下二者 的计算工作量之间的差别相对很小。另一方 面,读者应意识到,在较复杂的问题中,这两种 方法之间可能有显著的差别.如果图1-15所 图1-16。静不定系统. 示的系统,由于附加其他材料的杆件而制成更为复杂的系统(见图1-16中的 例子),那么用位移法按上面所述相同的方式进行求解依然是相当简单的,而 用力法求解则大为复杂,并需求解另外增加的联立方程。还有其他情形则相 反,用力法求解较为容易。 1.热效应和预应变效应 在静定结构中,整个结构上的均匀温度变化不产生任何应力, 因为它可以自由地膨张和收缩.另一方面,在一个以静不定方式 支承的结构中,温度变化将在杆件中产生应力,称为热应力、将一 根一端白由的杆件(如图1-7的例子)和另一根固定端杆件(图 1-17a)比较即可明了这一结论.在前一种情况下,作用在整个杆 ◆814