
杆的总伸长量为 fL P.do J0EA。 (1-9) 当方程(1-9)中积分号内的表达式 不易按闭型积分时,可采用数值法 计算积分.此外,对于锥形杆,只要 杆的两个侧边夹角很小,方程(19) 就会给出准确的结果、作为一个特 例,我们可以注意到,如果两侧边的 图1-9.其有变截而和1变轴力的杆. 夹角为20°,算出的正应力G=P/A 的最大误差仅为3%.对较小的夹角误差就更小,如果杆的锥度 很大时,就需用更精确的分析方法(见参考文献1-10). 桁架的变位 如果桁架每根杆件的长度变化为已知,那么简单行架芍 点的变位可用几何图形来确定.自然,该桁架每根杆作的长度变化可按已经 叙述的方法求出.为了说明求桁架变位的几何方法,让我们来确定图1-10 所示桁架中节点B的位移.桁架中两根杆件的力F和F。为 Fa=Pctgo F%o=Pesce 式中F为拉力,而F为压力.杆长的变化为 65=-PLas ctg日 EAab Bso=PLoccsc0 出1bo 为了确定B点的位移,我们首先假定A官杆伸长了一个量值8(见图 1-10b),因此其端点位于B1处.然后以A为圆心,以距离AB为半径作- 圆弧.由于B点的位移非常小,该圆弧可用通过B:而垂直于B杆轴的直 线米代替.类似地,假设BC杆缩短了一个量值ò,使其端点到达B2处然 后作以C为圆心、以距离CB,为半径作另一圆弧。此圆弧用通过点B,且垂 直于BO的直线来代替.此二垂线交于B处,它即为节点B的最终位置,因 此,自B至B的矢量就表示桁架节点B的位移⊙. 为了有助于进行计算,图1-10b的位移爸以较大的比例尺绘在图1-1e 中.我们从该图可以看出,。的水平分量为δ而其垂直分量由两部分 *原书中的正切、余切符号分别为a和cot,现根据我国国家标准《数学符号分 别改为g和ct绍。一译者注 ·180
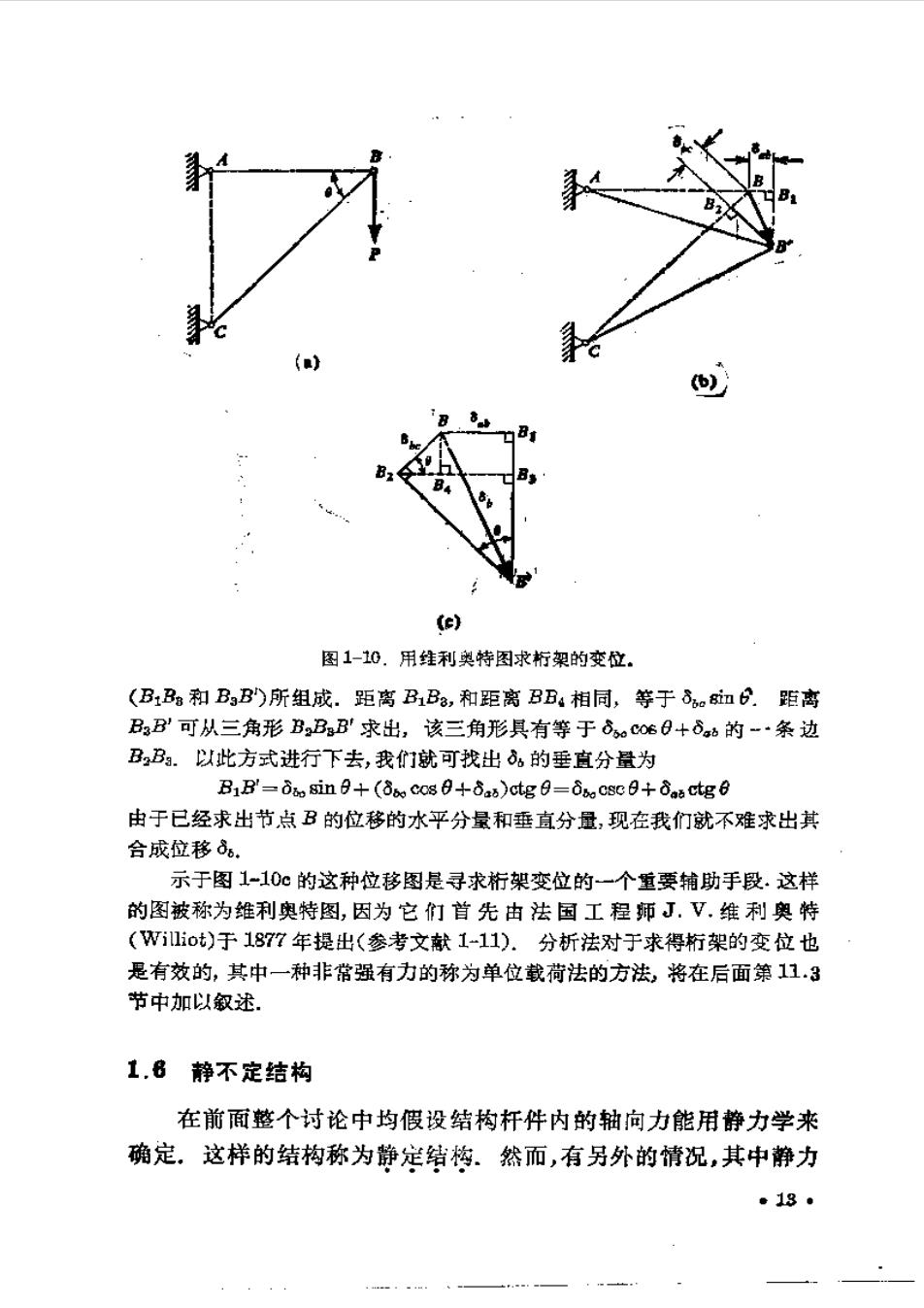
(e) 图1-10.用维利奥特图求桁架的变位 (B:B和BB)所组成.距离B1B8,和距离BB4相同,等于d。i如6.距离 B,B可从三角形B,BaB求出,该三角形具有等于6。oe日+8b的-·条边 B,B.以此方式进行下去,我们就可我出ò,的垂直分量为 B1B'=os sin0+(8o0 cos 04-6as)ctg 0=68o csc 0+8a8 ctg 由于已经求出节点B的位移的水平分量和垂直分量,现在我们就不难求出其 合成位移d. 示于图1-10加的这种位移图是寻求桁架变位的一个重要辅助手段.这样 的图被称为维利奥特图,因为它们首先由法国工程师J.V.维利奥特 (Williot)于187?年提出(参考文献1-11).分析法对于求得桁架的变位也 是有效的,其中一种非常强有力的称为单位载荷法的方法,将在后面第11.3 节中加以叙述 1.8静不定结构 在前面整个讨论中均假设结构杆件内的轴向力能用静力学来 确定。这样的结构称为静定结构.然而,有另外的情况,其中静力 e18●

平衡方程不足以确定全部杆力和支反力.对于这样的静不定结构, 只有当结构的位移考虑在内时,杆力和艾反力才能求出 图11-1a表示静不定结构的一个简单例子.杆AB的两端连 到刚性支承上,并在中间点©处沿轴向受到力P的作用.在杆的 端部将产生支反力。和,但这些反力不能只用静方力学求出·. 该杆的唯一静力乎衡方程为 R,+=P (a) 式中含有两个未知反力,因此对它们的算来说是不够的,必须根 据杆的变位得出第二个方程. R S R (b (a) 图1-11.静不定杆(用力法分析). 为了得到求解静不定问题所需要的补充方程,有两种通用的 方法可以使用.这两个方法都将用图1-11a中的杆件来说明.在 用第一种方法时,我们从选取反力之一作为未知量开始.在此例 中,让我们选取.如果这个量可以求出,那么另一反力R就 可根据静力学求得(见方程a).未知量R。称为静多余力,这是因 为如果将它移去,如图1-11b所示的那样,则余下的结构是静定的 而且是稳定的结构.因此,从建造一个能够承载的结构这一观点 来看,在A端的反力是不需要的,也就是说,它是多余的.放松多 "为了将反力与结构上的载荷相区别,通常横穿箭头画一截线或斜线来表示反 力,如图1-11a所示。 01在

余力之后而余下的结构称为放松结构,或基本结构, 现在让我们考虑载荷P对放松结构中A点位移的影响(图 1-11b).此位移等子 EA 且是向下指的.其次,考虑多余力。对于A点位移的影响(图 1-11o).注意,现在。已被想像成作用在放松结构上的载荷.由 于。,A点产生向上的位移为 RaL EA 由于P和R.同时作用时A点的最终位移8由联合6r与δx而 得.这样,若取向下位移为正,我们得到 8=6m-8m 由于A点的实际位移为零,上述方程变为 6e=8p (b) 或 RoL 。P6 田A 四A (o) 由此 (d) 从该方程求得R.后,我们就能根据静力学方程(方程a)求出R 这样,杆的两个反力就都求出来了. 上述用以分析静不定杆的方法可概括如下,选未知反力之一 为多余力,而后切断该杆并移去支座便之从结构中松开:然后,将 实际载荷P和多余力本身加在此静定且稳定的放松结构上。计算 由这两个量引起的位移,而后纳入位移协调方程(方程b)中.此协 湖方程表示有关变位的条件,“即在本例中变位⑧等于零.将以力 所表示的位移表达式代入协调方程(方程“)之后,我们可以解出 15
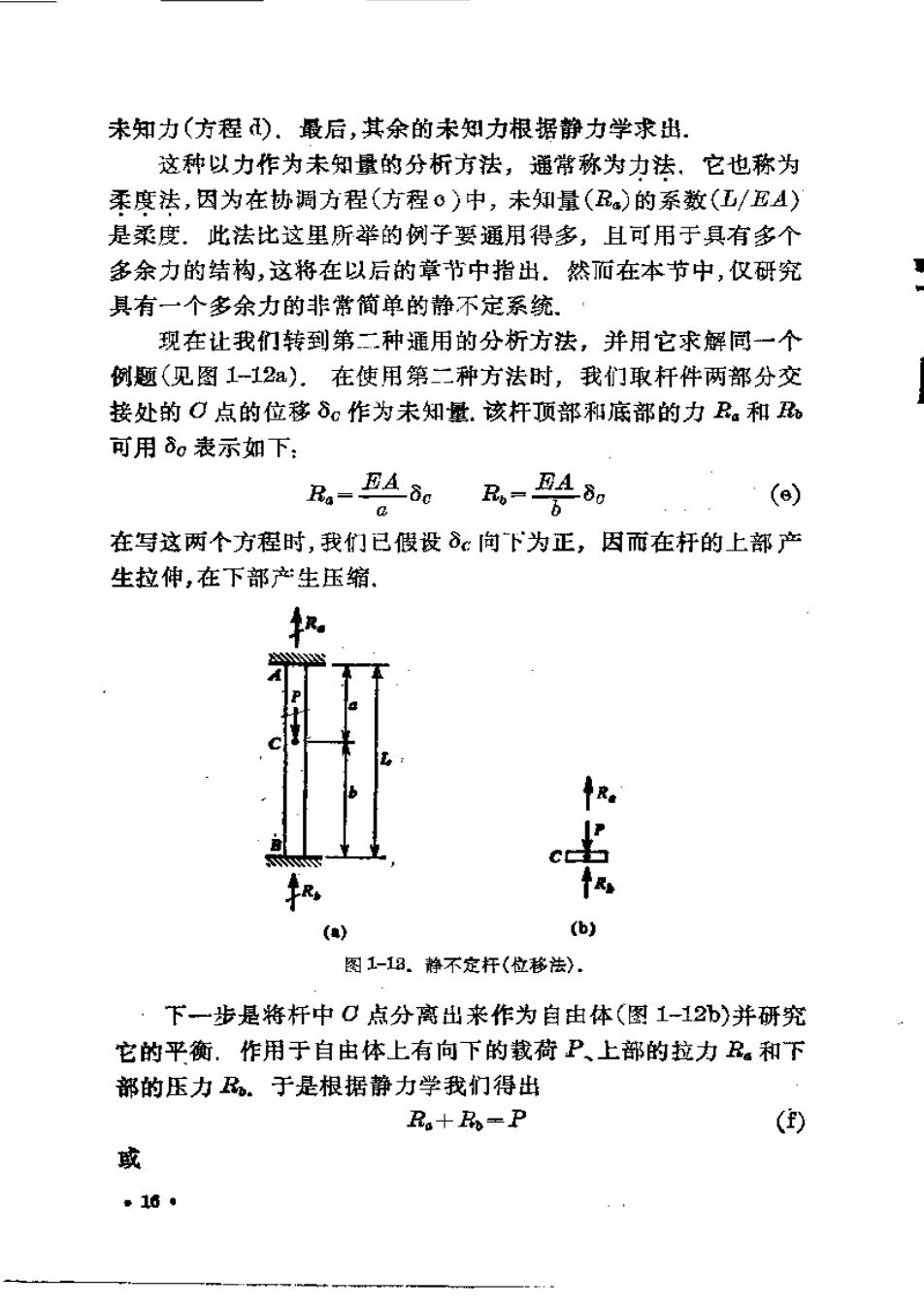
未知力(方程).最后,其余的未知力根据静力学求出。 这种以力作为未知量的分析方法,通常称为力法.它也称为 柔度法,因为在协调方程(方程o)中,未知量(五)的系数(工/EA)》 是柔度.此法比这里所举的例子要通用得多,且可用于具有多个 多余力的结构,这将在以后的章节中指出.然而在本节中,仪研究 具有一个多余力的非常简单的静不定系统 现在让我们转到第二种通用的分析方法,并用它求解同一个 例题(见图1-12a).在使用第二种方法时,我们取杆件两部分交 接处的O点的位移δc作为未知量.该杆顶部和底部的力R。和B 可用8。表示如下: Ra-EA So B=48 () 在写这两个方程时,我们已假设δ向下为正,因而在杆的上部产 生拉伸,在下部产生压缩 () (b) 图1-13.静不定杆(位移法》. 下一步是将杆中0点分离出来作为自由体(图1-12b)并研究 它的平衡.作用于自由体上有向下的载荷P、上部的拉力.和下 部的压力。于是根据静力学我门得出 R。十R=P () 或 16·