
安全系数来确定。这种作这通消用能凝土和木材之类的脆性材 料.一般来说,当根据容许应力进行设计时,可采用下列两式之- 得到其资用应力σ: co=g或co=g (1-3) 其中口和σu分别表示屈服点和极限应力,面和4为安全 系数.适当的安金系数的确定是一件复杂的事情,因为它取决子 所用材料的类型和结构的工作条件.当载荷是动态时(或突然作 用或大小变化),象出现在机器零件、飞机、桥梁等的载荷,由玻 劳破坏的可能性,就需要一个比同一结构承受静载荷时更大的安 全系数 代替使用容许应力的另一种方法是采用一个抵抗结构完全毁 坏的安全系数来设计结构.引起结构毁坏的载荷(或诸载荷)必须 首先予以确定,然后容许载荷(或资用载荷)由极限载荷除以适当 选择的载荷系数来确定,这种设计方法称为极限载荷设计,可以 看出,在此情况下,结构中实际应力的大小在确定其资用载荷时没 有起直接的作用.在设计金属结构时,资用应力法和极限载荷法 都是常用的.对于某些简单结构,其极限载荷的确定将在后面第 1.8节和9.5节中加以讨论. 1.4线性弹性和虎克定律 大多数结构材料在其应力一应变曲线上具有一个初始区段,在 此区段内材料呈现出既是弹性的又是线性的性态.在钢的应力一应 变图上从O到A这一这段(参看图1-2)就是一例.其他各例如 图14和1-5中的各曲线在比例极限以下的区段.当材料表现为 弹牲并且在应力和应变之间展现线性关系时,该材料就称为线性 弹性的.这是许多周体材料包括大多数金属、塑料、木材、混凝土 和陶土等的极为重要的性质 杆件受拉时,应力和应变之间的线性关系可用简单的方程来 表达 7
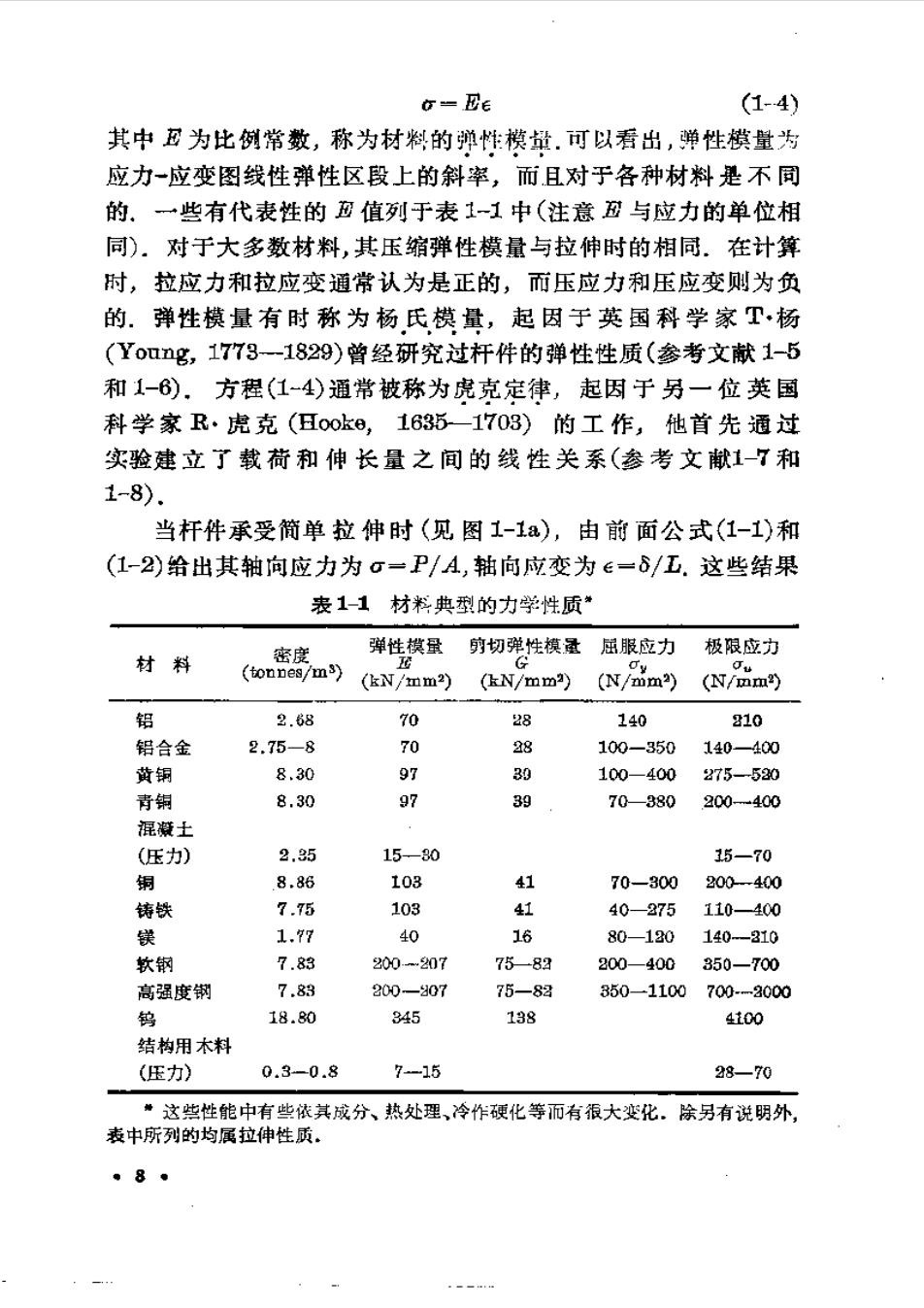
o-Ee (1-4) 其中为比例常数,称为材料的弹性:模量.可以看出,蝉性模量为 应力一应变图线性弹性区段上的斜率,而且对于各种材料是不同 的.一些有代表性的孢值列于表11中(注意面与应力的单位相 同)。对于大多数材料,其压缩弹性模量与拉伸时的相同.在计算 时,拉应力和拉应变通常认为是正的,而压应力和压应变则为负 的.弹性模量有时称为杨氏模量,起因于英国科学家T·杨 (Young,1773一1829)曾经研究过杆件的弹性性质(参考文献1-5 和1-6).方程(1~4)通常被称为虎克定律,起因于另一位英国 科学家R·虎克(五ook8,1635一1703)的工作,他首先通过 实验建立了载荷和伸长量之间的线性关系(参考文献1-7和 1-8). 当杆件承受简单拉伸时(见图1-1a),由前面公式(1-1)和 (1-2)给出其轴向应力为σ一P/A,轴向应变为∈=6/工.这些结果 表1-1材料典型的力学性质* 材料 密度 弹性模量 剪切弹性模量 屈服应力 极限应力 (tonnes/m3) u (kN/mm2) (kN/mm2) (N/mm2) (N/mam2) 铝 2.68 70 28 140 210 铅合金 2.75-8 70 28 100-350 140-400 黄铜 8.30 97 39 100-400 275-520 青铜 8.30 97 39 70—380 200400 混激土 (压力) 2.35 15-30 15-70 铜 8.86 103 41 70-300 200-400 铸铁 7.75 103 41 40-875 110-400 镁 1.77 40 16 80-120 140-310 软钢 7.83 200-…207 7583 200-400 350-700 高强度制 7.83 200-8307 75一88 350-1100 700-一2000 钨 18.80 345 138 4i00 结构用木料 (压力) 0.3-0.8 7-15 28-70 ”这些性能中有些依其成分、热处理、冷作硬化等而有很大变化。除另有说明外, 表中所列的均属拉伸性质. 。8●

与虎克定律(o二)联合,将给出杆件伸长量的下列方程 8-PL A (1-6) 该方程表明,线性弹性杆件的伸长量与载荷以及长度成正比,而与 弹性模量及横截面面积成反比.乘积丑A称为杆的轴向刚度 图11a中杆的柔度定义为由载荷的单位值所引起的变位,因 此我们从方程(1-5)看出,柔度为工/4.用类似的方式,杆的刚度 定义为产生单位变位所需要的力,因此,刚度等于A/工,即柔度 的倒数.后面在第十一章中将要说明,柔度和刚度在各种类型的结 构分析中都具有重要的作用. 泊松比 当一根杆件受到拉伸时,轴向伸长伴随有横向收 缩,亦即当杆的长度增大时其宽度变小。在弹性范围内,横向应变 与纵向应变之比为一常数,称为泊松比”,于是 横向应变 (1-6) 轴问应变 此常数是以著名法国数学家S.D.泊松(Poisson,1781一1840)而 命名的,他曾试图用材料的分子理论计算这个比值(参考文献 1-9).对于各个方向具有相同弹性性质的材料,即所谓各向同性 材料,泊松发现其=0.25.金属的实际试验表明,v通常在0.25 到0.36的范围内. 如果材料的泊松比和弹性模量为已知,杆受拉时的体积变化 就可以计算出来。体积变化在图1-6中画出,该图表示从受拉杆 中切出的一个微小的材料单元.该微元的原来形状由假定边长为 单位长度的立方体abedef gh给出.轴向力的方向通过图中所标的 应力心指出,单位立方体在载荷方向的伸长量为(等于σ/), 沿立方体两个刺边的缩短量为.因此,立方体的横截面面积按 比值(1一):1减小,而体积按比值(1+6)(1一e):1增大.把后 一比值的左端的乘积展开,然后略去包括∈的平方和立方的很小 的那些项,则此比值简化为(1+e一2e):1.该立方体的体积变化 等于最后体积减去最初体积,或∈(1一2).这个量称为单位体积 ◆9·
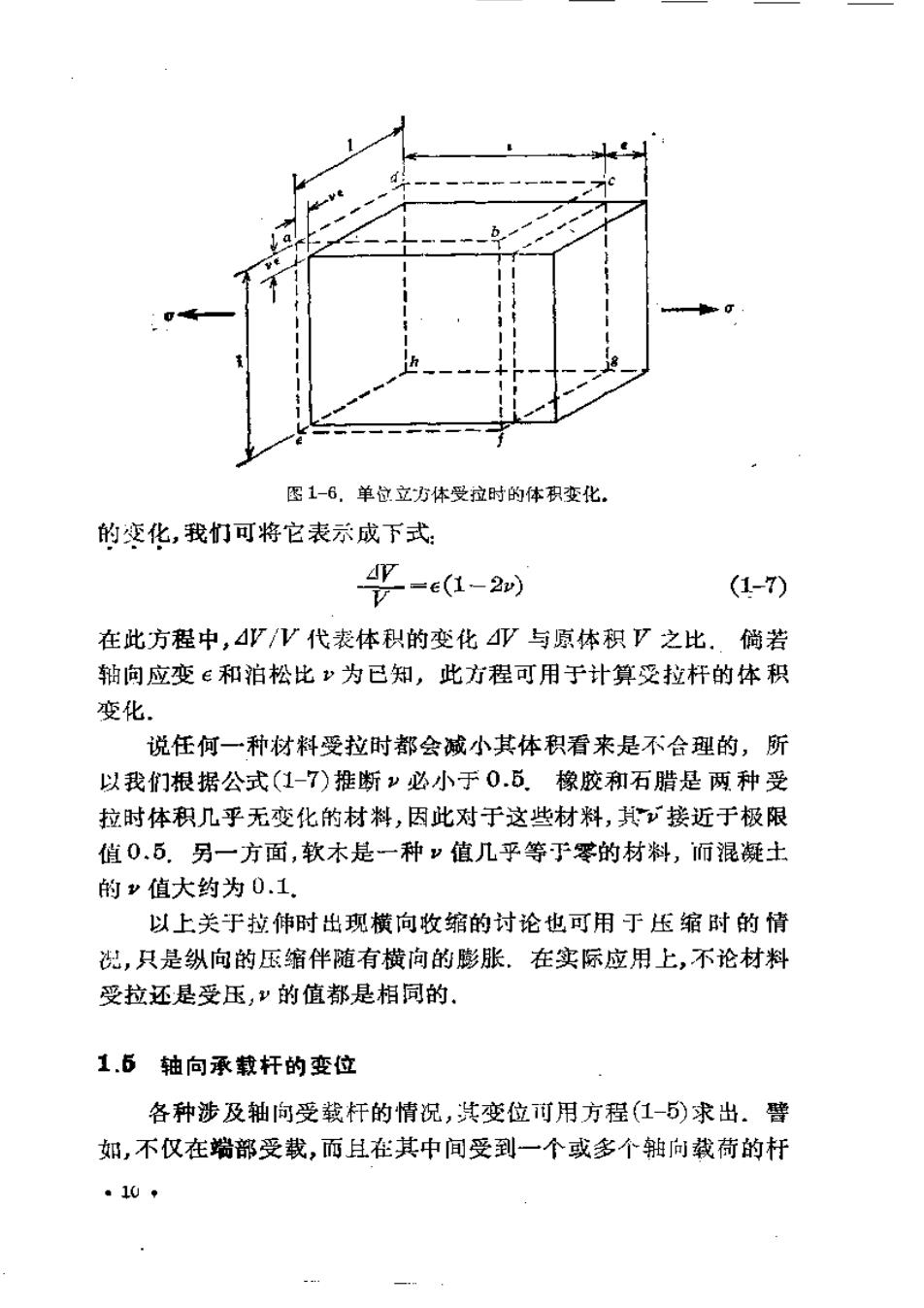
图1-6,单位立方体受拉时的体积变化 的变化,我们可将它表示成下式 AV -=e(1-2) (1-7) 在此方程中,AVV代表体积的变化少与原体积V之比.倘若 轴向应变e和泊松比”为已知,此方程可用于计算受拉杆的体积 变化. 说任何一种材料受拉时都会减小其体积看来是不合理的,所 以我们根据公式(1-7)推断”必小于0.5.橡胶和石腊是两种受 拉时体积几乎无变化的材料,因此对于这些材料,其接近于极限 值0.5.另一方面,软木是一种v值几乎等子零的材料,而混凝土 的y值大约为0.1」 以上关于拉伸时出现横向收缩的讨论也可用于压缩时的情 ,只是纵向的压缩伴随有横向的膨胀.在实际应用上,不论材料 受拉还是受压,)的值都是相同的. 1.5 轴向承载杆的变位 各种涉及轴向受载杆的情况,其变位可用方程(1-)求出.譬 如,不仅在端部受载,而且在其中间受到一个或多个轴向载荷的杆 ·10◆
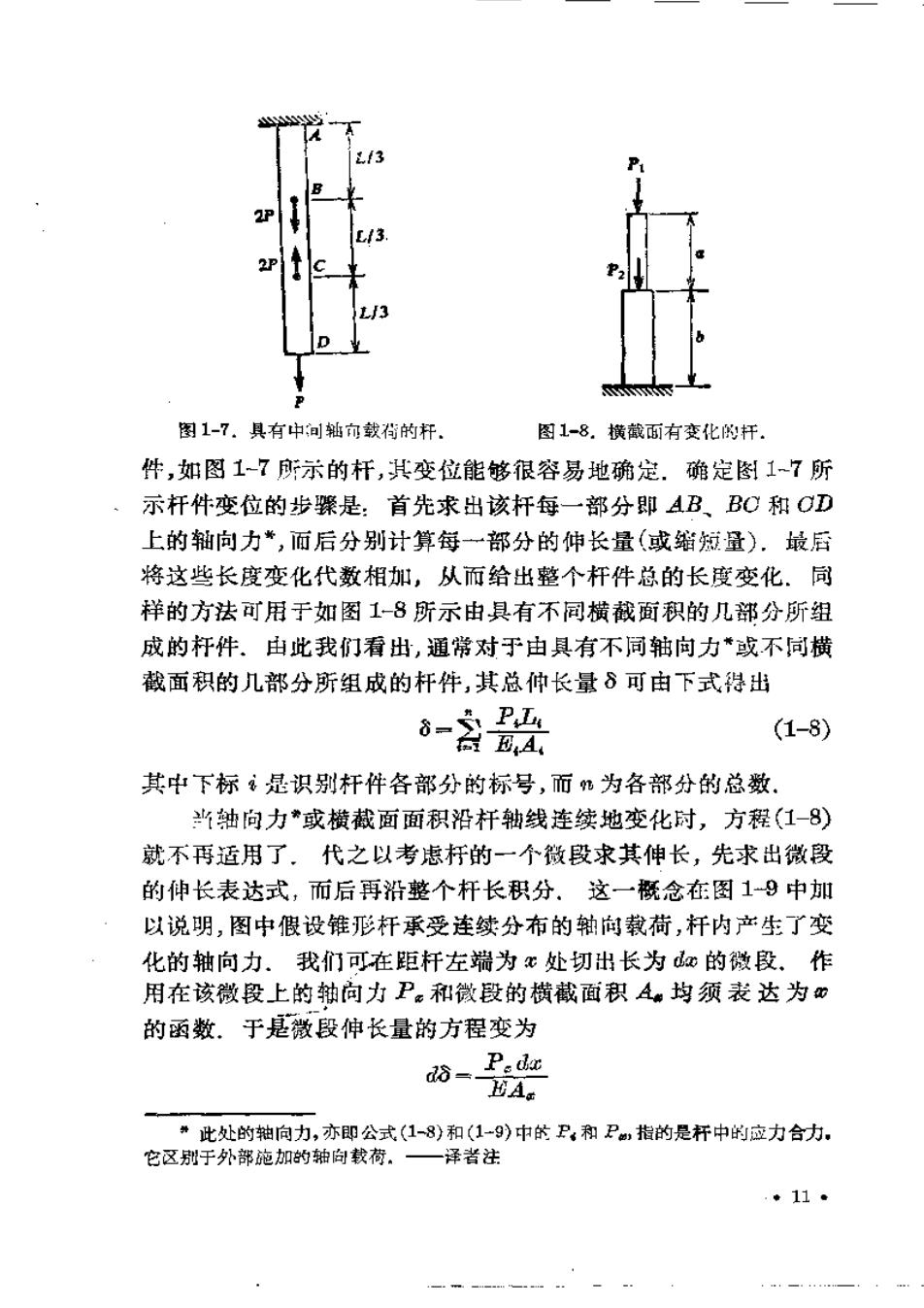
2好 图1-7.具有中间轴向载荷的杆, 图1-8。横截面有变化的杆。 件,如图1-7所示的杆,其变位能够很容易地确定.強定1-7所 、 示杆件变位的步骤是:首先求出该杆每一部分即AB、BO和CD 上的轴向力*,而后分别计算每一部分的仲长量(或缁拉量).最后 将这些长度变化代数相加:,从而给出整个杆件总的长度变化.同 样的方法可用于如图1-8所示由具有不同横截面积的几部分所组 成的杆件、由此我们看出,通常对于由具有不同轴向力或不同横 截面积的几部分所组成的杆件,其总仲长量6可由下式得出 8-5PL4 团A (1-8) 其中下标是识别杆件各部分的标号,而%为各部分的总数, 当轴向力*或横截面面积沿杆轴线连续地变化时,方程(1-8) 就不再适用了.代之以考虑杆的一个微段求其伸长,先求出微段 的伸长表达式,而后再沿整个杆长积分.这一概念在图19中加 以说明,图中假设锥形杆承受连续分布的轴向载荷,杆内产生了变 化的轴向力.我们可在距杆左端为x处切出长为a的微段.作 用在该微段上的轴向力P。和徵段的横截面积A。均须表达为心 的函数.于是微段伸长量的方程变为 d=_ eda HAs ”此处的轴向力,亦即公式(1-8)和(1一9)中的P,和P,指的是杆中的应力合力, 它区别于外部施加的轴向载荷。一泽者注 .◆11·