
随着我们学习本学科的进程,理论推导与实验所确定的材料 性质相结合的重要性将日趋明显.在本章中,我们将从讨论某些 基本概念着手,例如应力和应变,然后我们将研究承受拉伸、压缩 和剪切的简单结构元件的性态. 1.2 应力和应变 应力和应变的概念可通过研究一根棱柱形杆的拉伸(见图 1-1a)这一基本方法予以说明.棱柱形杆就是沿其整个长度具有 不变的横截面和直轴线的杆件.在此阐述中,假设杆的两端受到 使杆产生均匀伸长或拉仲的轴向力P.作一个与杆轴线相垂直 的人为切面(截面mm),我们就可以分离出杆的一部分作为自由 体(图1-1b).在其右端作用着拉力P,而在另一端存在着代表杆 件被移去部分对保留部分作用的诸力、这些力沿横截面连续分 布,就象液体静压力在淹没面上连续分布一样.该力的集度,亦 即单位面积上的力,称为应力,并且通常用希腊字母。来表示.假 设应力在整个横截面上均匀分布〔见图1-1b),我们就不难看出, 其合力等于集度σ乘以杆的横截面面积A.此外,根据图1-1b所 示物体的平衡,我们还能看出,这一合力必定与力P大小等而 方向相反.因此,我们得到 P (1-1) A m L (b) 图1-1.棱柱形杆受拉

此为棱柱形杆中均匀应力的方程。这一方程表明应力具有力除以 面积的单位一例如牛顿/平方毫米(N/m)*或磅力/平方英寸 (p).如图所示,当杆被力P拉神时,所产生的应力为拉应力: 如果将力反向而使杆件受到压缩,则称它们为压应力。 方程(1-1)成立的一个必要条件是应力。在杆的横截面上必 须是均匀的.如果轴向力P通过横截前的形心而作用,那么这一 条件就得以实现,这点可借静力学来证明(见习题1.2-1).当载 荷P不作用于形心时,杆将产生弯曲,需要作更复杂的分析(见第 .10节).但是,除非特别诣明,在本书中始终假设所有轴向力均 作用横截面的形心处.同样,除非另有说明,一般均假设物体自 身的重量略面不计,如在讨论图1-1中的杆件时所作的样」 承受轴向力的杆件的总伸长量将用希腊字母δ来表示(见图 1-1a),而单位长度的伸长量,亦即应变,用下式来确定: 6-2 (1-2 这里工为杆的总长度.注意应变6为一无量纲的量.只要应变沿 整个杆长是均匀的,就可以按公式(1-2)精确求得.如果杆件受拉, 此应变为拉应变,它代表材料伸长或拉伸;如果杆件受压,其应变 为压应变,这意味着杆件相邻的横截面彼此移近。 1.多拉伸试验 特定材料的应力与应变的关系是用拉伸试验来确定的.材料 的试件通常采用圆形杆件,它被置于拉神机上以承受拉力,杆上 所受的力和杆的伸长量都随着载荷的递增而予以量测。杆中的应 力是用杆的截面面积除其所受的力求得,而应变如由发生伸长的 长度除其伸长量求得.以此方式即得材料完整的应力一应变图, 结构钢应力-应变图的典型形状示于图1-2中,图中轴向应 变标在水平轴上,而相应的应力由曲线OAB心D的纵坐标给出. 从O到A,应力与应变之间成正比,其图形为线性的.过A点后 "1N/mm2=1M/m21Pa(兆帕).一一泽若注 ●3●
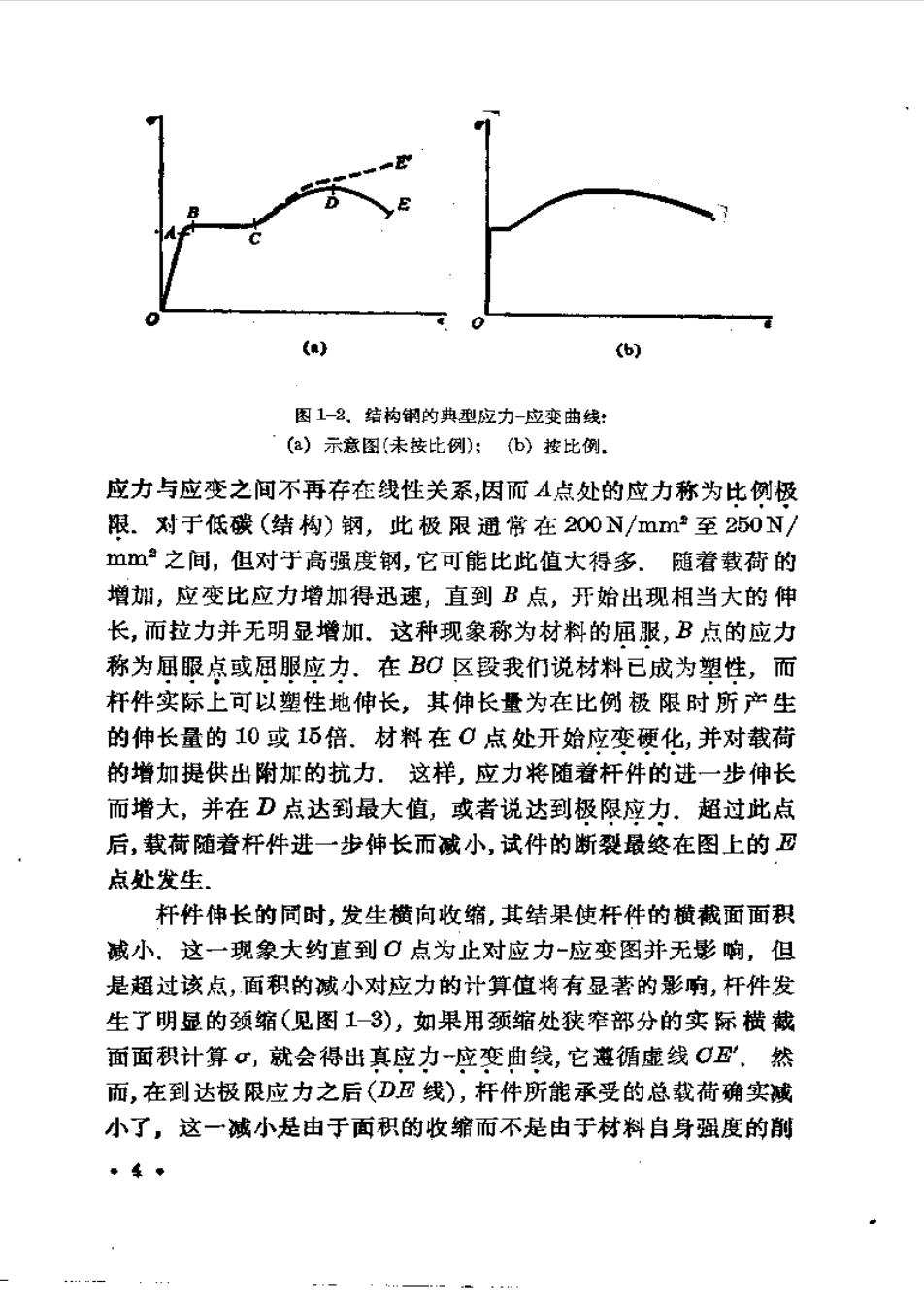
) 6b) 图1-2.结构钢的典型应力-应变曲线: (a)示意图(未按比例);(b)按比例. 应力与应变之间不再存在线性关系,因而A点处的应力称为比例极 限.对于低碳(结构)钢,此极限通常在200N/mm2至250N/ mm之间,但对于高强度钢,它可能比此值大得多.随着载荷的 增州,应变比应力增加得迅速,直到B点,开始出现相当大的伸 长,而拉力并无明显增加.这种现象称为材料的屈服,B点的应力 称为屈服点或屈服应力.在BO区段我们说材料已成为塑性,而 杆件实际上可以塑性地伸长,其伸长量为在比例极限时所产生 的伸长量的10或15倍.材料在0点处开始应变硬化,并对载荷 的增加提供出附加的抗力.这样,应力将随着杆件的进一步伸长 而增大,并在D点达到最大值,或者说达到极限应力.超过此点 后,载荷随着杆件进一步神长而减小,试件的断裂最终在图上的 点处发生, 杆件伸长的同时,发生横向收缩,其结果使杆件的横截面面积 减小.这一现象大约直到·点为止对应力-应变图并无影响,但 是超过该点,面积的械小对应力的计算值将有显著的影响,杆件发 生了明显的颈缩(见图1-3),如果用颈缩处狭窄部分的实标横截 面面积计算σ,就会得出真应力一应变曲线,它遵循虚线C.然 而,在到达极限应力之后(D.丑线),杆件所能承受的总载荷确实减 小了,这一诚小是由于面积的收缩而不是由于材料自身强度的削

图1-3.杆件受拉时的颈缩。 弱、直到被坏为止,材料在实际上都经得住应力的增加.然而,在 大多数实用场合,根据试件原横截面面积所得的常规应力一应变曲 线OABODE对设计应用来说提供了满意的数据. 图1-2a中的图线用来表明钢的应力-应变曲线的一殷特征, 但其比例不是真实的,因为正如已经指出的那样,从B到O发生 的应变可能大到从O至A所发生应变的15倍.另外,从0到 的应变甚至比从B到O的应变更大,用适当的比例所绘制的图 形示于图1-2b中.在该图中从O到A的应变与从A到的应 变相比小得无从看出,而图中的线性部分呈现为一条竖直线, 在明显的屈服点之后,随之有很大的塑性应变,这种现象在某 种程度上是钢所独有的,而钢是现代使用的最普通的结构金属.铝 合金在从线性到非线性这之间展现出一种更为渐进的过被,如图 1-4中的应力一应变图所示。钢和许多铝合金在破坏之前都将经 历很大的应变,所以被划归为延性材料.与之相反,脆性材料在较 低的应变值时就破坏(见图1-5).这种例子包括陶十、铸铁、混凝 土、某些金属合金和玻璃 对各种受压材料,亦可获得类似于拉伸时的图线,而且诸如比 图1-4.结构铝合金的典型 图1-5。脆性材料的典型应 应力应变曲线 力~应变曲线。 ·5

例极限、屈服点和极限应力等特征应力也可予以确定.对钢来说, 已发现其比例极限和屈服应力在受拉和受压时大致相等、当然, 对于许多脆性材料,受压时的特征应力要比受拉时大得多* 弹性 示于图1-2,1-4和1-5中的应力-应变图说明了各 种材料受拉时的性态。当材料的试件卸载时,亦即载荷逐渐减小 到零时,加载期间所产生的伸长会部分地或全部地消失,卸载过 程中趋向于恢复其原来形状的这种材料性质称为弹性.如果杆件 完全恢复其原状,称它是完全弹性的;如果仅部分回复其原状,它 就是部分弹性的.在后一种情况中,当载荷移去后残留在杆中的 伸长称为求久变形 当进行材料的拉伸试验时,载荷可以到某个(小的)选定值 而后把它移去.划果没有永久变形,亦即杆中的应变回到零,则材 料直到该选定载荷值所代表的应力之前都是弹性的.这种载和 御载的过程可对逐次增试的载荷值反复地进行.最后,应力总会 达到某个数值,使卸载过程中并非全部应变都得以恢复.用这一 方法可以确定弹性范围内的上限应力,这一应力称为弹性极限.对 于钢以及许多其它金属,其弹性极限比例极限几予重.然而, 对于橡胶之类的材料,弹性性质可以延续到远远超过其比例极 根。 容许应力 在设计结构时,需要保证结构在工作条件下,充 分发挥它在建造时预期的作用.从结构承载能力这一观点出发, 结构中的最大应力通常应保持在低于其比例极限,因为只有这样, 当施加载荷而后移去时才不会有永久变形.估计到结构有偶候的 超载以及制港中有可能不准确烈结构分祈中可能的未变量,过 常用选择低于比例极限的容许应力(或资用应力)以提供安全落 数.例如,在结构钢设计中,对屈服点为250N/mm°的钢通常采 用拉伸容许应力为165N/mm2.因此,抵抗屈服的安全系数为 1.2.也有其他一些情况,其中资用应力是用对极限妒!寂延当的 *应力-应芝为冬布.们勞利(co山ernoulli,154一1705)利lJ,V.蓬斯 莱(Ponc8let,1788一18)房创始,见参考文献1-4, 有6