§1图的基本概念与模型 ,网络(赋权图) 设图G={V,E},对G的每一条边yH相应赋予数量指标w, w称为边[的权,赋予权的图G称为网络(或赋权图)。 权可以代表距离、费用、通过能力(容量)等等。 端点无序的赋权图称为无向网络,端点有序的赋权图称为有 向网络。 15 4 14 20 ⑧ 2014-12-15 25 6
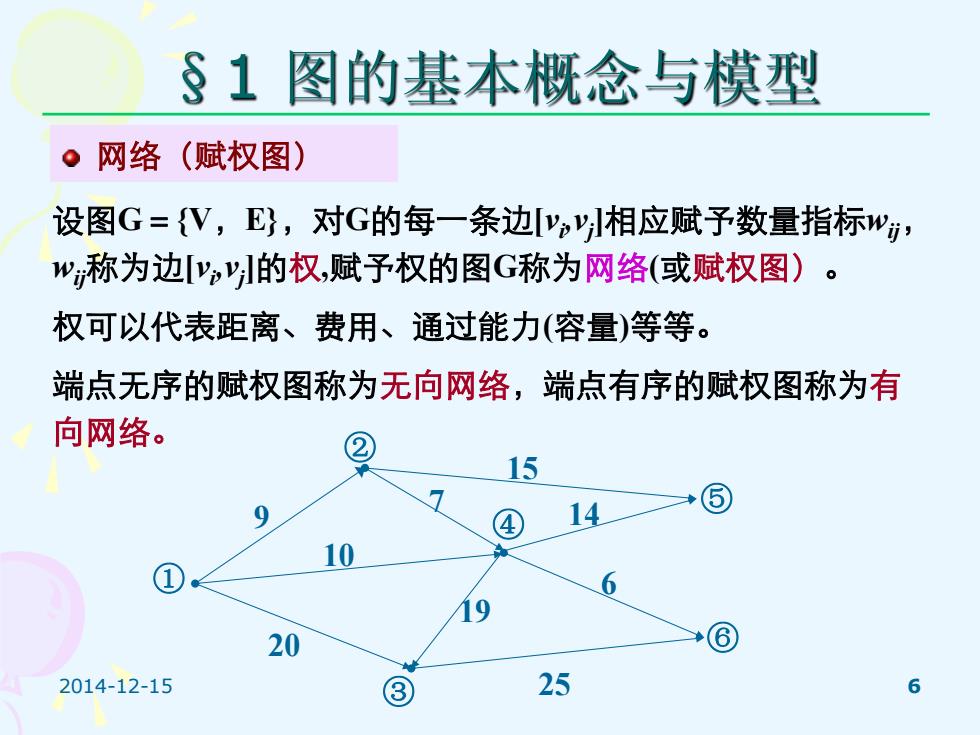
2014-12-15 6 §1 图的基本概念与模型 网络(赋权图) 设图G={V,E},对G的每一条边[vi ,vj ]相应赋予数量指标wij, wij称为边[vi ,vj ]的权,赋予权的图G称为网络(或赋权图)。 权可以代表距离、费用、通过能力(容量)等等。 端点无序的赋权图称为无向网络,端点有序的赋权图称为有 向网络。 ① ② ③ ④ ⑤ ⑥ 9 10 20 15 7 14 19 25 6
§1图的基本概念与模型 定义:图中的点用v表示,边用e表示。对 每条边可用它所连接的点表示,记作: e1=[v1,V1];e2=[v1,v2]。 ·端点,关联边,相邻 % 若有边e可表示为e=y,以,称v和y 06 8 e7 是边e的端点,反之称边e为点y,或y 的关联边。若点",与同一条边关 联,称点v和v,相邻;若边e和e具 有公共的端点,称边e,和e相邻。 2014-12-15
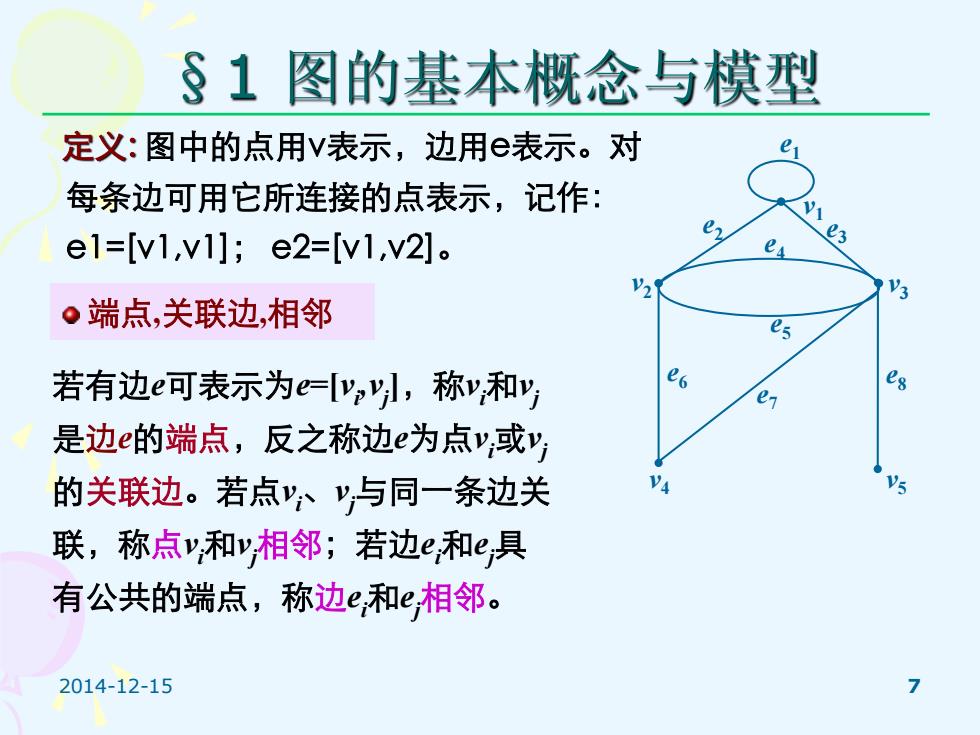
2014-12-15 7 §1 图的基本概念与模型 v3 e7 e4 e8 e5 e6 e1 e2 e3 v1 v2 v4 v5 定义: 图中的点用v表示,边用e表示。对 每条边可用它所连接的点表示,记作: e1=[v1,v1]; e2=[v1,v2]。 端点,关联边,相邻 若有边e可表示为e=[vi ,vj ],称vi和vj 是边e的端点,反之称边e为点vi或vj 的关联边。若点vi、vj与同一条边关 联,称点vi和vj相邻;若边ei和ej具 有公共的端点,称边ei和ej相邻
§1图的基本概念与模型 。环,多重边,简单图 如果边e的两个端点相重,称该边为 e 环。如右图中边e,为环。 如果两个点之间多于一条,称为多重 es e6 边,如右图中的e4和es。 er 对无环、无多重边的图称作简单图。 一个无环,有多重边的图称为多重图。 2014-12-15 8
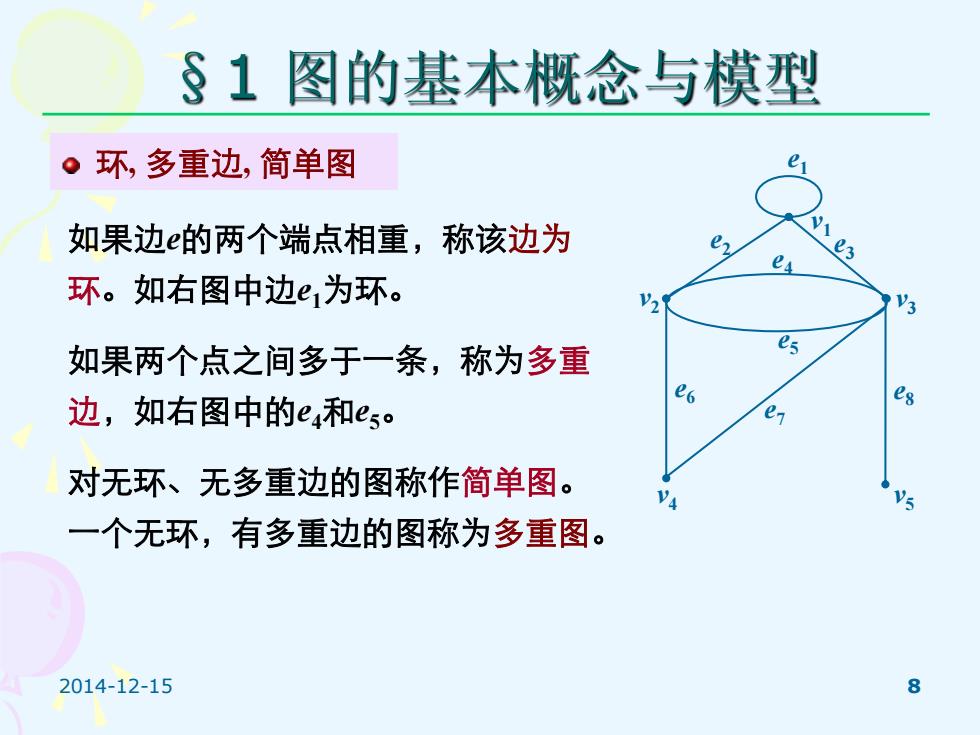
2014-12-15 8 §1 图的基本概念与模型 环, 多重边, 简单图 如果边e的两个端点相重,称该边为 环。如右图中边e1为环。 如果两个点之间多于一条,称为多重 边,如右图中的e4和e5。 对无环、无多重边的图称作简单图。 一个无环,有多重边的图称为多重图。 v3 e7 e4 e8 e5 e6 e1 e2 e3 v1 v2 v4 v5
§1图的基本概念与模型 。次,奇点,偶点,孤立点 与某一个点v,相关联的边的数目称为 e 点的次(也叫做度),记作()。 右图中d(v)=4,d(V3)=5,d(vs)=1。次 es 为奇数的点称作奇点,次为偶数的 e 点称作偶点,次为1的点称为悬挂点, 次为0的点称作孤立点。 图的次:一个图的次等于各点的次之和。 2014-12-15 9
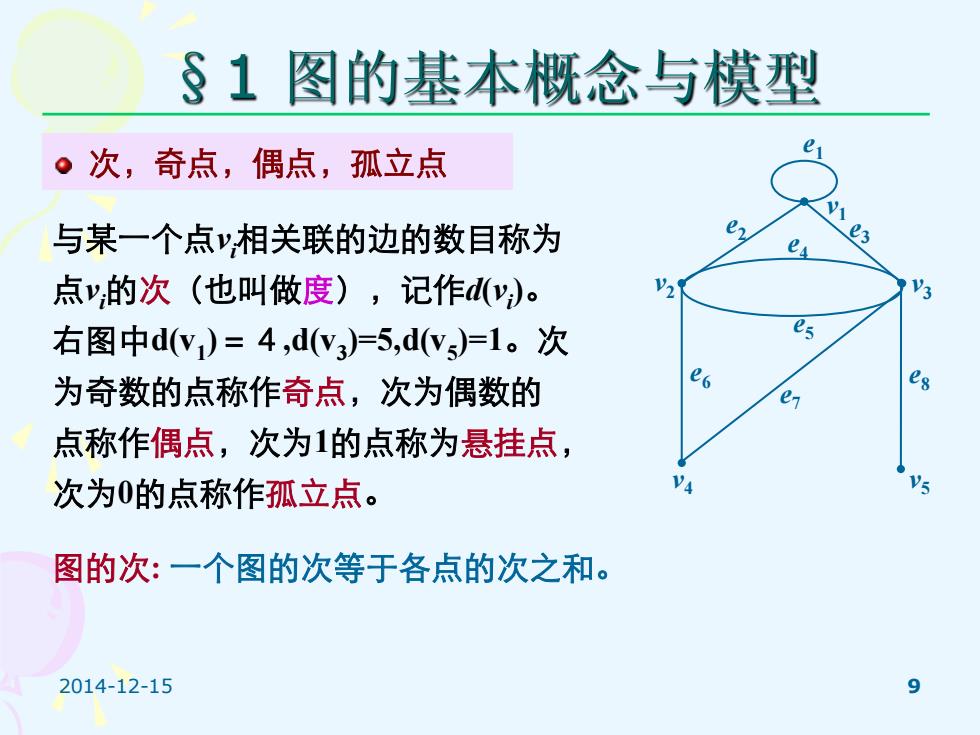
2014-12-15 9 §1 图的基本概念与模型 次,奇点,偶点,孤立点 与某一个点vi相关联的边的数目称为 点vi的次(也叫做度),记作d(vi )。 右图中d(v1 )=4,d(v3 )=5,d(v5 )=1。次 为奇数的点称作奇点,次为偶数的 点称作偶点,次为1的点称为悬挂点, 次为0的点称作孤立点。 v3 e7 e4 e8 e5 e6 e1 e2 e3 v1 v2 v4 v5 图的次: 一个图的次等于各点的次之和

§1图的基本概念与模型 出次与入次 有向图中,以:为始点的边数称为点y的出次,用d()表 示;以为终点的边数称为点y:的入次,用表示d(W);:点 的出次和入次之和就是该点的次。 ※有向图中,所有顶点的入次之和等于所有顶点的出次之 和。 2014-12-15 10
2014-12-15 10 §1 图的基本概念与模型 出次与入次 有向图中,以vi为始点的边数称为点vi的出次,用d + (vi )表 示;以vi为终点的边数称为点vi 的入次,用表示d - (vi ) ;vi 点 的出次和入次之和就是该点的次。 ※ 有向图中,所有顶点的入次之和等于所有顶点的出次之 和