西安电子科技大学：《信号检测与估值》课程教学资源（课件讲稿，2019）第三章 统计信号估计（主讲：郑贱平）

最小均方误差估计 选定的代价函数为 d@)-le-oj dOx)=[c)poxkio =0-6)ploo 求解方法 使条件平均代价最小的一个必要条件是对上式中日求偏导 令偏导为零来求得最佳的估计量日 信号检测与估值2019年秋季 11

最小均方误差估计 选定的代价函数为     2 ˆ ~ c                C  x  c  p  x d ~ ˆ             p  x d 2 ˆ 使条件平均代价最小的 个必要条件是对上式中  ˆ 求偏导 求解方法 使条件平均代价最小的 一个必要条件是对上式中  求偏导 令偏导为零来求得最佳的估计量  ˆ 信号检测与估值 2019年秋季 11

最小均方误差估计 ado ab -品6-6itw =品上g-20+rb0nso =-2gpx0+20pl0rH02a=0 .opoHio 信号检测与估值2019年秋季 12

最小均方误差估计     ˆ ˆ   C x                  p x d 2 ˆ ˆ                       p x d 2 2 ˆ ˆ 2 ˆ       0 ˆ 2 2 ˆ ˆ             mse p d p d     x    x     1     p  x d         mse  p  x d ˆ 信号检测与估值 2019年秋季 12  

最小均方误差估计 ae=Ccplglxlh0 注： 1.最小均方误差估计的估计量实际是条件均值 日e=rpxa0=Elolx] 2最小均方误差估计的条件平均代价实际是条件方差 C..x)=0-0poxde=0-Elo)ploo 3.最小均方误差估计量的另一种形式 o-pHo -Lopdo p(x) ople.x)do po)poHo p(O.x)de Lp(e)p(xode 信号检测与估值2019年秋季 13

最小均方误差估计      mse  p  x d ˆ     mse p 注： 1.最小均方误差估计的估计量实际是条件均值    d E     ˆ p  x d E  x  mse     2.最小均方误差估计的条件平均代价实际是条件方差           Cmse  x    mse p  x d 2 ˆ ˆ             E  x p  x d 2 3.最小均方误差估计量的另一种形式        mse  p  x d ˆ             d p p x , x p                   p d p d x , x                       p p d p p d x x 信号检测与估值 2019年秋季 13     p , x d       p  p x  d

最大后验估计 选定的代价盛数为c例=0-)-2A2 0,a<△/2 Clox)="cO)p(oxHao =」p(el)d0+ap(oa0 -1-p(0)do p(ol)do-xp(os) 使条件平均代价最小，应该使 rx0取到太值 当△很小时，为保证上式最大，应当选择估计量B, 使它处于后验概率密度函数p(x)最大值的位置。 信号检测与估值2019年秋季 14

最大后验估计     1, / 2 ˆ c c              选定的代价函数为     0, / 2            C  x  c  p  x d ~ ˆ     ˆ 2 ˆ 2 p d pd                x x ˆ    ˆ 2 ˆ 2 1 p d            x     ˆ 2 ˆ 2 ˆ p dp            x x 使条件平均代价最小，应该使 取到最大值        2 ˆ 2 ˆ   p  x d 2 当  很小时，为保证上式最大，应当选择估计量 ， ˆ 使它处于后验概率密度函数 p x最大值的位置。 信号检测与估值 2019年秋季 14 使它处于后验概率密度函数 p x最大值的位置

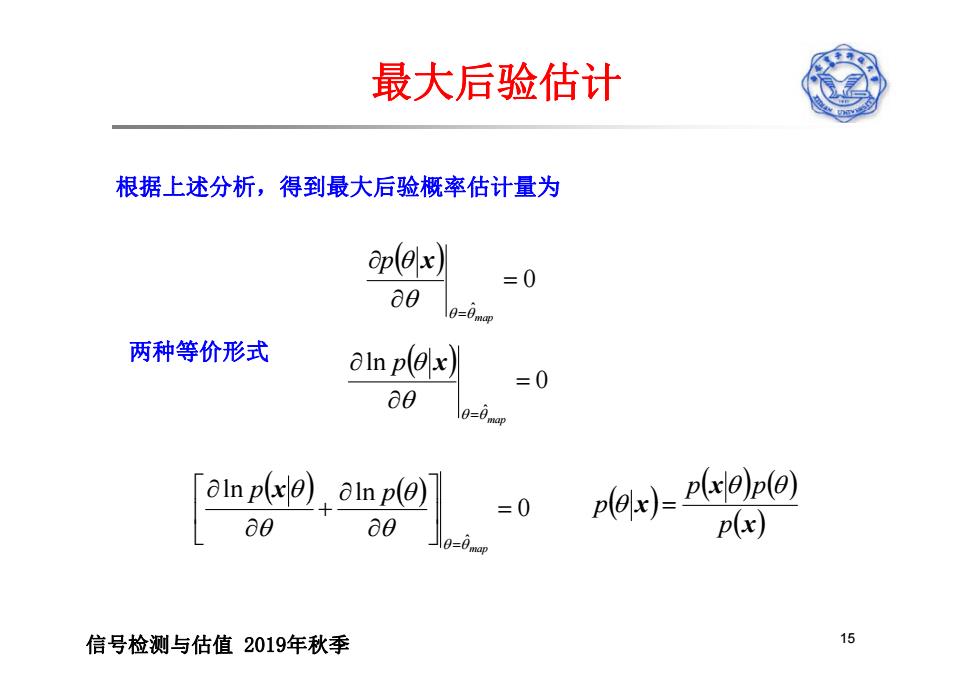
最大后验估计 根据上述分析，得到最大后验概率估计量为 ap(ox) =0 a0 O-Omap 两种等价形式 ainp(ox) =0 a0 Q-0mop ainp(xo)ainp(e) =0 plox)-e)p(o) a0 a0 p(x) 信号检测与估值2019年秋季 15

最大后验估计 根据上述分析 得到最大后验概率估计量为 p x 根据上述分析，得到最大后验概率估计量为   0 ˆ     map p     x 两种等价形式   0 ln ˆ     map p     x p     0 ln ln   p x  p    x    x p p p         0 ˆ         map p p       x x p p   信号检测与估值 2019年秋季 15