
3.1节:矩阵的三角分解 证:(1)因为A的秩为m,所以A的m个行向量a1,a2,·,am线性无 关且m≤n. 从而可在线性空间C中选取向量组am+1,Qm+2,·,an使得 a1,02,…,an线性无关 类似于定理1的证明,将a1,a2,·,an斯密特正交化、单位化得标准 正交向量组31,B2,·,Bn 于是有 4口+40在色是QC 矩阵理论课程组(数学科学学院)】 矩阵理论 2021年9月13/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 证:(1) 因为 A 的秩为 m, 所以 A 的 m 个行向量 α1, α2, · · · , αm 线性无 关且 m ≤ n. 从而可在线性空间 C n 中选取向量组 αm+1, αm+2, · · · , αn 使得 α1, α2, · · · , αn 线性无关. 类似于定理 1 的证明,将 α1, α2, · · · , αn 斯密特正交化、单位化得标准 正交向量组 β1, β2, · · · , βn. 于是有 其中 L 为 m 阶正线下三角复矩阵和 U 为 n 阶酉矩阵. 类似地可证明 (2) 成立. 我们用 U m×n m 表示以 m 个两两正交的单位行向量组成的矩阵的集合, 用 U m×n n 表示以 n 个两两正交的单位列向量组成的矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 13 / 61

3.1节:矩阵的三角分解 证:(1)因为A的秩为m,所以A的m个行向量a1,a2,·,am线性无 关且m≤n. 从而可在线性空间C中选取向量组am+1,Qm+2,·,an使得 a1,02,…,an线性无关 类似于定理1的证明,将a1,a2,·,an斯密特正交化、单位化得标准 正交向量组51,B2,·,Bn 于是有 其中L为m阶正线下三角复矩阵和U为n阶酉矩阵 类似地可证明(2)成立 口+4y,之是,是QQ 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月13/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 证:(1) 因为 A 的秩为 m, 所以 A 的 m 个行向量 α1, α2, · · · , αm 线性无 关且 m ≤ n. 从而可在线性空间 C n 中选取向量组 αm+1, αm+2, · · · , αn 使得 α1, α2, · · · , αn 线性无关. 类似于定理 1 的证明,将 α1, α2, · · · , αn 斯密特正交化、单位化得标准 正交向量组 β1, β2, · · · , βn. 于是有 其中 L 为 m 阶正线下三角复矩阵和 U 为 n 阶酉矩阵. 类似地可证明 (2) 成立. 我们用 U m×n m 表示以 m 个两两正交的单位行向量组成的矩阵的集合, 用 U m×n n 表示以 n 个两两正交的单位列向量组成的矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 13 / 61

3.1节:矩阵的三角分解 证:(1)因为A的秩为m,所以A的m个行向量a1,a2,·,am线性无 关且m≤n. 从而可在线性空间C中选取向量组am+1,Qm+2,·,an使得 a1,02,…,an线性无关 类似于定理1的证明,将1,a2,·,an斯密特正交化、单位化得标准 正交向量组31,B2,·,Bn 于是有 其中L为m阶正线下三角复矩阵和U为n阶酉矩阵, 类似地可证明(2)成立, 我们用Umxn表示以m个两两正交的单位行向量组成的矩阵的集合, 用Umx”表示以n个两两正交的单位列向量组成的矩阵的集合 生0Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月13/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 证:(1) 因为 A 的秩为 m, 所以 A 的 m 个行向量 α1, α2, · · · , αm 线性无 关且 m ≤ n. 从而可在线性空间 C n 中选取向量组 αm+1, αm+2, · · · , αn 使得 α1, α2, · · · , αn 线性无关. 类似于定理 1 的证明,将 α1, α2, · · · , αn 斯密特正交化、单位化得标准 正交向量组 β1, β2, · · · , βn. 于是有 其中 L 为 m 阶正线下三角复矩阵和 U 为 n 阶酉矩阵. 类似地可证明 (2) 成立. 我们用 U m×n m 表示以 m 个两两正交的单位行向量组成的矩阵的集合, 用 U m×n n 表示以 n 个两两正交的单位列向量组成的矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 13 / 61
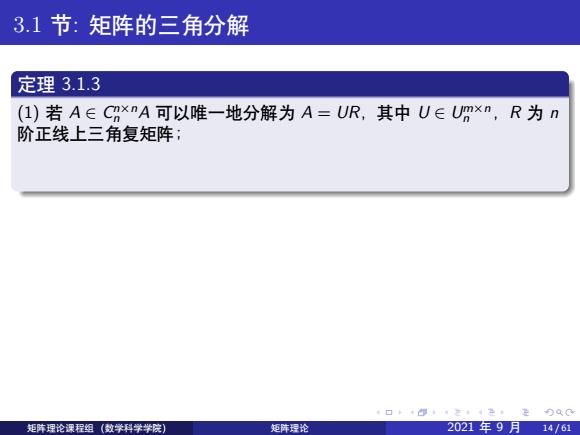
3.1节:矩阵的三角分解 定理3.1.3 (1)若A∈CxnA可以唯一地分解为A=UR,其中U∈Umxn,R为n 阶正线上三角复矩阵; 4口+40在色是QC 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月14/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定理 3.1.3 (1) 若 A ∈ C n×n n A 可以唯一地分解为 A = UR,其中 U ∈ U m×n n ,R 为 n 阶正线上三角复矩阵; (2) 若 A ∈ C m×n m ,则 A 可以唯一地分解为 A = LU,其中 U ∈ U m×n m ,L 为 n 阶正线下三角复矩阵. 证:(1) 因为 A ∈ C m×n n ,将矩阵 A 列向量组做斯密特正交化、单位化, 类似于定理 1 的证明,可得 A = UR. 再证明唯一性:因为 A ∈ C m×n n ,所以对任意 n 维向量 x ̸= 0,有 Ax ̸= 0,因此 x HA HAx = (Ax) HAx > 0,于是 A HA 为正定 Hermite 矩阵. 设 A = U1R1 = U2R2,其中 U1,U2 ∈ U m×n n ,R1, R2 为 n 阶正线上三角 复矩阵,则 U H 1 U1 = U H 2 U2 = En. 故 A HA = (U1R1) HU1R1 = (U2R2) HU2R2 = R H 1 R1 = R H 2 R2. 由推论 2 知 R1 = R2. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 14 / 61
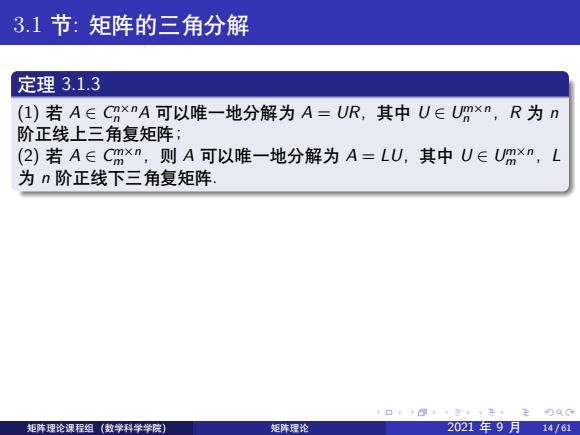
3.1节:矩阵的三角分解 定理3.1.3 (1)若A∈CxnA可以唯一地分解为A=UR,其中U∈U四xn,R为n 阶正线上三角复矩阵; (2)若A∈Cmxn,则A可以唯一地分解为A=LU,其中U∈Umxn,L 为n阶正线下三角复矩阵 口卡+①三·是空Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月14/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定理 3.1.3 (1) 若 A ∈ C n×n n A 可以唯一地分解为 A = UR,其中 U ∈ U m×n n ,R 为 n 阶正线上三角复矩阵; (2) 若 A ∈ C m×n m ,则 A 可以唯一地分解为 A = LU,其中 U ∈ U m×n m ,L 为 n 阶正线下三角复矩阵. 证:(1) 因为 A ∈ C m×n n ,将矩阵 A 列向量组做斯密特正交化、单位化, 类似于定理 1 的证明,可得 A = UR. 再证明唯一性:因为 A ∈ C m×n n ,所以对任意 n 维向量 x ̸= 0,有 Ax ̸= 0,因此 x HA HAx = (Ax) HAx > 0,于是 A HA 为正定 Hermite 矩阵. 设 A = U1R1 = U2R2,其中 U1,U2 ∈ U m×n n ,R1, R2 为 n 阶正线上三角 复矩阵,则 U H 1 U1 = U H 2 U2 = En. 故 A HA = (U1R1) HU1R1 = (U2R2) HU2R2 = R H 1 R1 = R H 2 R2. 由推论 2 知 R1 = R2. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 14 / 61