
第8章数字通信中的信道编码 国 片=禹++无。+写 ④ 校验节点 5=无+无+无+ 国 变量节点 (a) (b) 图&-42LDPC码校验方程及其Tanner图 Tanner图中的“圈被定义为Tanner图中由一个顶点出发,最后又回到同样顶点的一系 列边”组成的环。在环中同层节点不允许互连,而且除了起点和终点,中间顶点只允许出现 一次。圈的边数称为“圈长”。 图8-4-2(a)中粗线所示的就是一个圈长为8的圈。Tanner图中最小的圈长被称为girth” 对线性分组码而言,Tanner图中不存在长度为2或者奇数的环,所以Tanner图的最小圈长 至少是4,即girth≥4。Tanner图上圈长越大,码的性能越好。 ②因子图 因子图是一个二部图,是广义的Tanner图,用于图形表示一多变量函数的因式分解。 假如函数u,vxy)可以分解为 fu,xy,=fi,fcy动f② (8-4-1) 则其因子图表示如图843所示。 2 图84-3多变量函数的因子图表示 因子图通常由节点、边和半边(只与单个节点相连的边)组成。因子图一般满足: (a)每一个因子对应唯一一个节点 (b)每一个变量对应唯一一个边或半边 ()变量所对应的边与因子所对应的节点相连的条件是因子是变量的函数 由此可知,在因子图表示中,任何变量不会在多于2个因子中出现。因子有时也称为 局部函数,它们的乘积称为全局变量。在上式中∫为全局函数,人、方为局部函数(因子)。 西安电子科技大学 16
第 8 章 数字通信中的信道编码 西安电子科技大学 16 C1 C2 C3 C4 V1 V2 V3 V4 V5 V6 V7 V8 校验节点 变量节点 (a) (b) 图 8-4-2 LDPC 码校验方程及其 Tanner 图 Tanner 图中的“圈”被定义为 Tanner 图中由一个顶点出发,最后又回到同样顶点的一系 列“边”组成的环。在环中同层节点不允许互连,而且除了起点和终点,中间顶点只允许出现 一次。圈的边数称为“圈长”。 图 8-4-2(a)中粗线所示的就是一个圈长为 8 的圈。Tanner 图中最小的圈长被称为“girth”。 对线性分组码而言,Tanner 图中不存在长度为 2 或者奇数的环,所以 Tanner 图的最小圈长 至少是 4,即 girth ≥ 4。Tanner 图上圈长越大,码的性能越好。 ②因子图 因子图是一个二部图,是广义的 Tanner 图,用于图形表示一多变量函数的因式分解。 假如函数 f(u,v,x,y,z)可以分解为 f(u,v,x,y,z)=f1(u,v,x)f2(x,y,z)f3(z) (8-4-1) 则其因子图表示如图 8-4-3 所示。 u f1 v x y z f2 f3 图 8-4-3 多变量函数的因子图表示 因子图通常由节点、边和半边(只与单个节点相连的边)组成。因子图一般满足: (a) 每一个因子对应唯一一个节点 (b) 每一个变量对应唯一一个边或半边 (c) 变量所对应的边与因子所对应的节点相连的条件是因子是变量的函数 由此可知,在因子图表示中,任何变量不会在多于 2 个因子中出现。因子有时也称为 局部函数,它们的乘积称为全局变量。在上式中 f 为全局函数,f1、f2、f3为局部函数(因子)
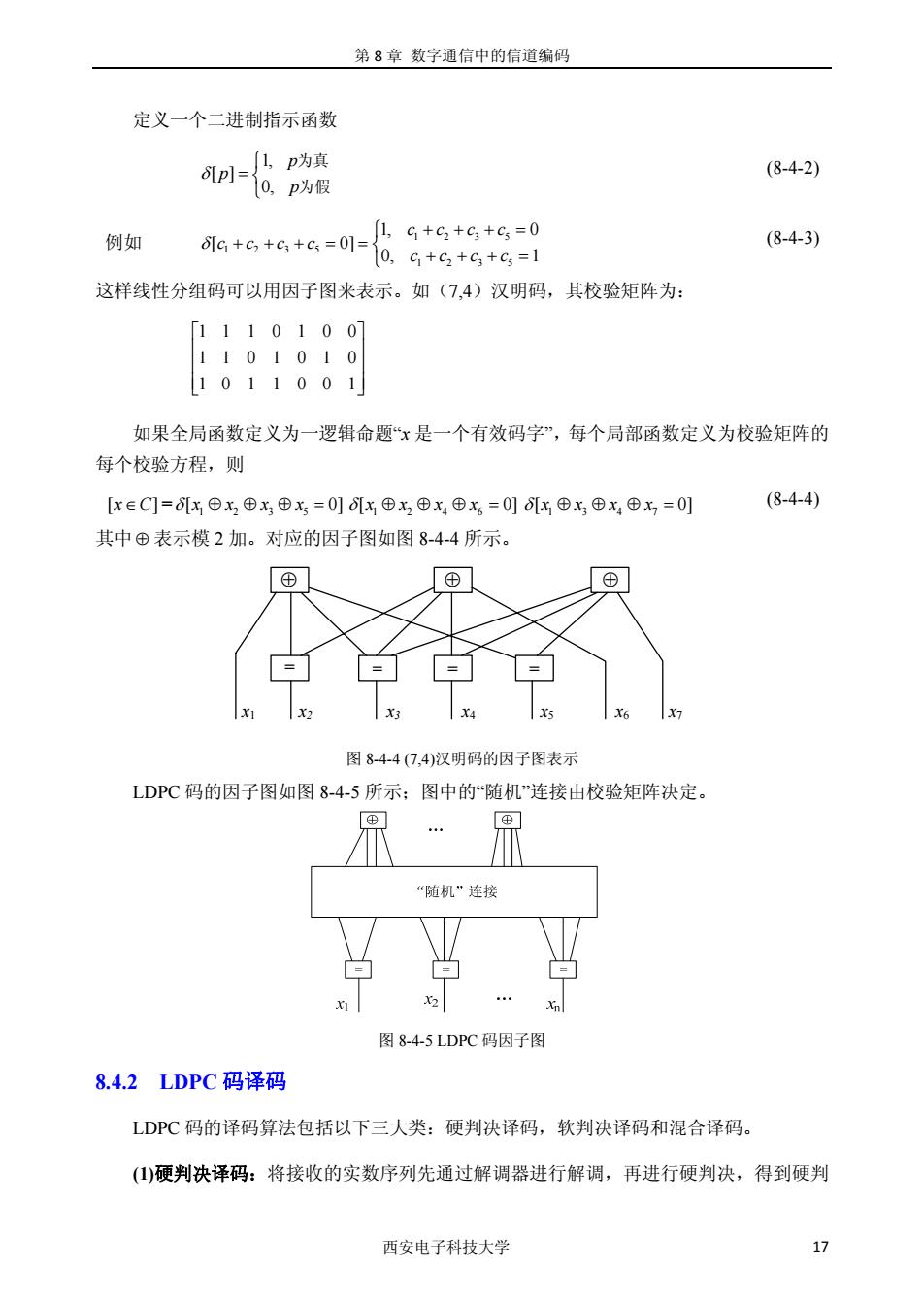
第8章数字通信中的信道编码 定义一个二进制指示函数 nl- (8-4-2) 例如 G+g+6+6=01=9+6+6+6=0 (8-4-3) 0,c+c2+c3+c=1 这样线性分组码可以用因子图来表示。如(7,4)汉明码,其校验矩阵为: 1110100] 1101010 1011001 如果全局函数定义为一逻辑命题“x是一个有效码字”,每个局部函数定义为校验矩阵的 每个校验方程,则 x∈C=x⊕x⊕x田x=0]6x⊕x⊕x,⊕x6=0]6x⊕X⊕x⊕x,=0] (8-4-4) 其中⊕表示模2加。对应的因子图如图84-4所示。 ⊕ ⊕ ⊕ 图8-44(7,4)汉明码的因子图表示 LDPC码的因子图如图8-4-5所示:图中的“随机”连接由校验矩阵决定。 “随机”连接 白 世 图8-45LDPC码因子图 8.4.2LDPC码译码 LDC码的译码算法包括以下三大类:硬判决译码,软判决译码和混合译码。 ()硬判决译码:将接收的实数序列先通过解调器进行解调,再进行硬判决,得到硬判 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 17 定义一个二进制指示函数 1, [ ] 0, p p p δ ⎧ = ⎨ ⎩ 为真 为假 (8-4-2) 例如 1235 1235 1235 1, 0 [ 0] 0, 1 cccc cccc cccc δ ⎧ + ++= +++= = ⎨ ⎩ + ++= (8-4-3) 这样线性分组码可以用因子图来表示。如(7,4)汉明码,其校验矩阵为: 1110100 1101010 1011001 ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 如果全局函数定义为一逻辑命题“x 是一个有效码字”,每个局部函数定义为校验矩阵的 每个校验方程,则 [ ] x ∈C = 1235 δ[ 0] xxxx ⊕⊕⊕= 1246 δ[ 0] xxxx ⊕ ⊕⊕= 1347 δ[ 0] xxxx ⊕ ⊕⊕= (8-4-4) 其中⊕ 表示模 2 加。对应的因子图如图 8-4-4 所示。 = = = = ⊕ ⊕ ⊕ x1 x2 x3 x4 x5 x6 x7 图 8-4-4 (7,4)汉明码的因子图表示 LDPC 码的因子图如图 8-4-5 所示;图中的“随机”连接由校验矩阵决定。 图 8-4-5 LDPC 码因子图 8.4.2 LDPC 码译码 LDPC 码的译码算法包括以下三大类:硬判决译码,软判决译码和混合译码。 (1)硬判决译码:将接收的实数序列先通过解调器进行解调,再进行硬判决,得到硬判

第8章数字通信中的信道编码 决0,1序列,最后将得到的硬判决序列输送到硬判决译码器进行译码。这种方式的计算复杂 度固然很低,但是硬判决操作会损失掉大部分的信道信息,导致信道信息利用率很低,硬 判决译码的信道信息利用率和译码复杂度是三大类译码中最低的。常见的硬判决译码算法 有比特翻转(bit-ipping,.BF)算法、一步大数逻辑(onc-step majority-logic,OSMLG)译 码算法。 2)软判决译码:可以看成是无穷比特量化译码,它充分利用接收的信道信息(软信息) 信道信息利用率得到了极大的提高,软判决译码利用的信道信息不仅包括信道信息的符号, 也包括信道信息的幅度值。软判决译码的信道信息利用率和译码复杂度是三大类译码中最 高的。最常用的软判决译码算法是和积译码算法,又称置信传播(belief propagation,BP) 算法。 (3)混合译码:混合译码结合了软判决译码和硬判决译码的特点,是一类基于可靠度的 译码算法,它在硬判决译码的基础上,利用部分信道信息进行可靠度的计算。常用的混合 译码算法有、加权比特翻转(weighted BF,WBF)算法、加权OSMLG(weighted OSMLG, WMLG)译码算法。 和积译码对每个译码符号的可靠度采用对数似然比来衡量。 L(z)=log(pl=0) p(x=1) 如果p(x=0))>p(x=1),则为正,而且值越大,意味着p)=0, 的可能性更大: 如果p(x=1)>pt=0),则的为负,而且值越小,意味者 p(x=1)的可能性更大: 因此,(x)的正负性表示x的硬判决,而幅度表示判决的可靠性。 这里主要介绍和积译码算法(也称为置信传播算法)。 ·和积译码算法 ◆和积算法是一种软判决消息传递算法,消息沿着在Tanner图(或因子图)的边进行传 递,可用来计算与全局函数相关的各种边缘函数。 ◆这种消息传递算法也称为迭代译码算法,因为消息在变量节点和校验节点间前后不断 传递,直到条件满足为止。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 18 决 0,1 序列,最后将得到的硬判决序列输送到硬判决译码器进行译码。这种方式的计算复杂 度固然很低,但是硬判决操作会损失掉大部分的信道信息,导致信道信息利用率很低,硬 判决译码的信道信息利用率和译码复杂度是三大类译码中最低的。常见的硬判决译码算法 有比特翻转(bit-flipping, BF)算法、一步大数逻辑(one-step majority-logic, OSMLG)译 码算法。 (2)软判决译码:可以看成是无穷比特量化译码,它充分利用接收的信道信息(软信息), 信道信息利用率得到了极大的提高,软判决译码利用的信道信息不仅包括信道信息的符号, 也包括信道信息的幅度值。软判决译码的信道信息利用率和译码复杂度是三大类译码中最 高的。最常用的软判决译码算法是和积译码算法,又称置信传播 (belief propagation, BP) 算法。 (3) 混合译码:混合译码结合了软判决译码和硬判决译码的特点,是一类基于可靠度的 译码算法,它在硬判决译码的基础上,利用部分信道信息进行可靠度的计算。常用的混合 译码算法有、加权比特翻转(weighted BF, WBF)算法、加权 OSMLG(weighted OSMLG, WMLG)译码算法。 和积译码对每个译码符号的可靠度采用对数似然比来衡量。 如果 ,则 L(x)为正,而且值越大,意味着 的可能性更大; 如 果 , 则 L(x) 为负,而且值越小,意味着 的可能性更大; 因此,L(x)的正负性表示 x 的硬判决,而幅度表示判决的可靠性。 这里主要介绍和积译码算法(也称为置信传播算法)。 z 和积译码算法 和积算法是一种软判决消息传递算法,消息沿着在 Tanner 图(或因子图)的边进行传 递,可用来计算与全局函数相关的各种边缘函数。 这种消息传递算法也称为迭代译码算法,因为消息在变量节点和校验节点间前后不断 传递,直到条件满足为止

第8章数字通信中的信道编码 ◆对于LDPC译码,如果传递的消息为二进制的,则为比特翻转译码(硬判决),如果 传递的消息是关于码字比特置信度的概率,则译码为置信传播译码(BP算法,软判 决)。当表示置信度的概率值表示为对数似然比,这时的BP译码通常称为和积译码, 因为对数似然比使得变量节点和校验节点的计算至涉及加法与乘法。 ◆输入比特概率称为接收比特的先验概率,对于二进制变量x,其对数使然比定义为 L(x)=log(p(x=0)/p(x=1)). ◆和积译码算法的目的是用于计算每一码字比特的最大后验概率(MAP),通过校验约 束获取的比特的额外信息称为外信息,对应的比特的先验概率称为内信息。 ◆如果Tanner图无环,则通过和积译码获得的后验概率是准确的,否则和积算法只能通 过迭代获取后验概率的近似值。这主要是由于环路会使外部信息与比特先验概率之间 有一定的相关性。 ◆每次译码迭代过程中,信息节点(或子节点)向校验节点(或父节点)传递信息,校 验节点将更新过的信息又传递给信息节点。 图8-4-6给出了消息传递过程的示意图。 ”图()中,信息节点1传递给校验节点c的信息,是由节点m从信道获取的信息 加上与节点相连的其它校验节点(如图中的c、c2)的信息组成的。信息节点 对这些输入信息进行处理后传递给校验节点©3。 对于软判决,该信息是一种概率(准确的说是取某值的可靠性或置信度),即给定 输入信息y,节点取值0、1的概率P(v=by),b∈{0,1}。 ◆同样,如图8-46b)所示,校验节点c传递给信息节点的信息,是由本节点从其 它信息节点(图中的、2、)获取的信息信息组成的,经处理后传递给信息节 点4。 ◆传递的信息为校验节点c1在获取输入信息后校验方程c1满足的概率,即p(校验方程 c1成立输入信息)。 6 ○2 ○ (@)消息节点传递信息给校验节点 (b)校验节点传递信息给消息节点 图8-4-6BP算法消息传递 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 19 对于 LDPC 译码,如果传递的消息为二进制的,则为比特翻转译码(硬判决),如果 传递的消息是关于码字比特置信度的概率,则译码为置信传播译码(BP 算法,软判 决)。当表示置信度的概率值表示为对数似然比,这时的 BP 译码通常称为和积译码, 因为对数似然比使得变量节点和校验节点的计算至涉及加法与乘法。 输入比特概率称为接收比特的先验概率,对于二进制变量 x,其对数使然比定义为 Lx px px ( ) log ( 0) / ( 1) = == ( ) 。 和积译码算法的目的是用于计算每一码字比特的最大后验概率(MAP),通过校验约 束获取的比特 i 的额外信息称为外信息,对应的比特的先验概率称为内信息。 如果 Tanner 图无环,则通过和积译码获得的后验概率是准确的,否则和积算法只能通 过迭代获取后验概率的近似值。这主要是由于环路会使外部信息与比特先验概率之间 有一定的相关性。 每次译码迭代过程中,信息节点(或子节点)向校验节点(或父节点)传递信息,校 验节点将更新过的信息又传递给信息节点。 图 8-4-6 给出了消息传递过程的示意图。 图(a)中,信息节点 v1传递给校验节点 c3的信息,是由节点 v1 从信道获取的信息 y1, 加上与节点 v1 相连的其它校验节点(如图中的 c1、c2)的信息组成的。信息节点 v1 对这些输入信息进行处理后传递给校验节点 c3。 对于软判决,该信息是一种概率(准确的说是取某值的可靠性或置信度),即给定 输入信息 y,节点 v1取值 0、1 的概率 P(v1=b|y),b∈{0,1}。 同样,如图 8-4-6(b)所示,校验节点 c1传递给信息节点 v4的信息,是由本节点从其 它信息节点(图中的 v1、v2、v3)获取的信息信息组成的,经处理后传递给信息节 点 v4。 传递的信息为校验节点 c1 在获取输入信息后校验方程 c1 满足的概率,即 p(校验方程 c1 成立|输入信息)。 (a) 消息节点传递信息给校验节点 (b)校验节点传递信息给消息节点 图 8-4-6 BP 算法消息传递

第8章数字通信中的信道编码 为推导译码过程,做如下标记: 信息节点或比特节点用表示,校验节点用/表示 ,表示校验节点j传递给变量节点1的外部概率信息: 9,表示变量节点i传递给校验节点j外部概率信息: C,表示与变量节点i相连的校验节点的集合,即C:h=l; 号表示与校验节点j相连的变量节点的集合,即={任h,1 Cy表示除j外与变量节点i相连的校验节点的集合: i表示除i外与校验节点j相量节点的集合。 【引理】二进制序列a(a1,a2.,a,其中Pa=1)=P,则a中包含偶数个1的概率为 立计护0-2n.a中包含奇数个1的米是写加0-29 依据引理,若比特1为1且比特1满足校验方程j的概率为 %-号0-2p (8-4-5) 其中P表示对于节点了,比特”为1的概率估计。 这样,比特1为0且比特i满足校验方程j的概率为1P,定义对数似然比 -u} 作号a-2p的 5n-2p (8-4-6) 利用等式m传e,2》1-2p得 log +a,) (8-4-7) -Πamla,2小 其中g=LLR(Pm)=lOgI-Pm)/P)。 利用等式2p)=s华)84)式可写为 n-2 m(,2列 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 20 为推导译码过程,做如下标记: 信息节点或比特节点用 i 表示,校验节点用 j 表示 rj,i表示校验节点 j 传递给变量节点 i 的外部概率信息; qi,j表示变量节点 i 传递给校验节点 j 外部概率信息; Ci表示与变量节点 i 相连的校验节点的集合,即 Ci={j:hji=1}; Vj表示与校验节点 j 相连的变量节点的集合,即 Vi={i:hji=1}; Ci\j 表示除 j 外与变量节点 i 相连的校验节点的集合; Vj\i 表示除 i 外与校验节点 j 相量节点的集合。 【引理】 二进制序列 a=(a1,a2,.,an),其中 P(ak=1)=Pk,则 a 中包含偶数个 1 的概率为 1 1 1 (1 2 ) 2 2 n k k p = + − ∏ ,a 中包含奇数个 1 的概率是 1 1 1 (1 2 ) 2 2 n k k p = − − ∏ 。 依据引理,若比特 i 为 1 且比特 i 满足校验方程 j 的概率为 ' ' int , , \ 1 1 (1 2 ) 2 2 j ext ji j i iVi P p ∈ =− − ∏ (8-4-5) 其中 ' int j,i p 表示对于节点 j,比特 i’为 1 的概率估计。 这样,比特 i 为 0 且比特 i 满足校验方程 j 的概率为 1- , ext Pj i ,定义对数似然比 , , , , 1 ( ) log ext ext j i ji ji ext j i P r LLR P P ⎛ ⎞ − = = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = ' ' ' ' int , \ int , \ 1 1 (1 2 ) 2 2 log 1 1 (1 2 ) 2 2 j j j i iVi j i iVi p p ∈ ∈ ⎛ ⎞ ⎜ ⎟ + − − − ⎝ ⎠ ∏ ∏ (8-4-6) 利用等式 1 1 tanh log 1 2 2 p p p ⎛ ⎞ ⎛ ⎞ − ⎜ ⎟ ⎜ ⎟ = − ⎝ ⎠ ⎝ ⎠ 得 ( ) ( ) ' ' ' ' , \ , , \ 1 tanh / 2 log 1 tanh / 2 j j j i iVi j i j i iVi q r q ∈ ∈ ⎛ ⎞ ⎜ ⎟ + = − ⎝ ⎠ ∏ ∏ (8-4-7) 其中 ' j i, q =LLR( ' int j i, P )= ( ' ' ) int int , , log (1 ) / ji ji − P P 。 利用等式 1 1 2 tanh ( ) log 1 p p p − ⎛ ⎞ + = ⎜ ⎟ ⎝ ⎠ − , (8-4-7) 式可写为 ( ) ' ' 1 , , \ 2 tanh tanh / 2 j j i j i iVi r q − ∈ ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ ∏ (8-4-8)