
第8章数字通信中的信道编码 码字 C E C,+E, C;+E, C,+E2 禁用码字 C2+E3 C,+E3 C,+E, E C,+E C+E 由于陪集首和伴随式有一一对应的关系,而这些陪集首实际上也就代表着可纠正的错 误图样,因此可以通过计算伴随式来找到陪集首(即错误图样),然后完成纠错。 综上所述,利用伴随式译码表译码的步骤是: (1)计算接收矢量R的伴随式S=RH。 (2)根据计算出的伴随式找出对应的陪集首龙(这是根据S作出的E的估值)。 (3)码字估值C=R+E被认为是发送码字。 【例】(7,4)汉明码译码示例 由伴随式的定义可知,S=EH,汉明(7,4)码的校验矩阵为: 「1110100 1101010 (8-3-21) 1011001 这样我们可以得到伴随式与错误图样的关系。 表8-3-3(7,4)码件随式与错误图样关系表 、 0000 00. 0 00, 00 00 100 0 10000 11 1010, 0 000 0 111 例如,设发送码字信息元(0010)对应的码字(0010101),接收码字为R=(0000101), (即实际错误图样为E=(001000),R的伴随式为: 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 11 码字 C1 (E1) C2 . Ci . 2 C k E2 C 2 + E 2 . C i + E 2 . 2 C k + E 2 E3 C 2 + E 3 . C i + E 3 . 2 C k + E 3 # # # # # # 禁 用 码 字 2 E n k− 2 2 C E+ n k− . 2n k C E i + − . 2 2 C E k nk + − 由于陪集首和伴随式有一一对应的关系,而这些陪集首实际上也就代表着可纠正的错 误图样,因此可以通过计算伴随式来找到陪集首(即错误图样),然后完成纠错。 综上所述,利用伴随式译码表译码的步骤是: (1)计算接收矢量 R 的伴随式 S = RHT 。 (2)根据计算出的伴随式找出对应的陪集首 Eˆ (这是根据 S 作出的 E 的估值)。 (3)码字估值Cˆ = R + Eˆ 被认为是发送码字。 【例】(7,4)汉明码译码示例 由伴随式的定义可知,S=EHT ,汉明(7,4)码的校验矩阵为: H= 1110100 1101010 1011001 ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ (8-3-21) 这样我们可以得到伴随式与错误图样的关系。 表 8-3-3 (7,4)码伴随式与错误图样关系表 E S e6 e5 e4 e3 e2 e1 e0 s2 s1 s0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 1 1 1 例如,设发送码字信息元(0010)对应的码字(0010101),接收码字为 R =(0000101), (即实际错误图样为 E =(001000)),R 的伴随式为:

第8章数字通信中的信道编码 [111 110 101 S=RH=0000101 011 101 (8-3-22) 100 010 001 从表8-3-3中找到与=(110)相对应的错误图样(陪集首)为(001000),于是译码输出为 C=(0000101)+(001000)=(0010101) (8-3-23) 纠正了错误,译码正确。 若相同的码字经传输得R=(1000101),其错误图样为E”=(1010000),伴随式为S= (011),由表8-3-3求得 E=(0001000) (8-3-24) 这时C=(1000101+(0001000)=(1001101)≠C,译码是错误的,原因是E不是标准阵列的陪集 首。究其原因这种(们,4)码的dm=3,它可纠正任何一位差错,而不能纠正两位差错。 总之,线性码正确译码的充要条件是信道实际错误图样是标准阵列的陪集首,这个结 论对任何线性分组码的译码方法都适用。 8.3.5一些特殊的线性分组码 (1)汉明码 汉明码有二进制的,也有非二进制的。二进制汉明码的共同特性是(m,k)=(2-12-m-1), m是校验位数,可取大于1任意整数。这些码的最小码间距离为3。伴随式译码特别适合于 汉明码。例如m=3,则得(7,4)汉明码,如前述例子:其最小码距d。=3,即最多可纠正 1位错码。汉明码如果再加上一位对所有码元都进行校验的监督位,则监督码元由m增至m +1,信息位不变,码长由2-1增至2,通常把这种(2,2"-1-m)码称为扩展汉明码。 扩展汉明码的最小码距增加为4,能纠正1位错误同时检测2位错误。 (2)Hadamard码 哈达马矩阵Mn是一个由0”和1”构成的n×n矩阵,构造方法如下: N-2时,4-007 「MM 「M.Mn1 01' ,依此类推,M.M。 哈达马矩阵每行就是一个Walsh序列,Hadamard码可成对选取MnM.的行向量,构成 码长为n的(m,)线性分组码,该码由2n个码字组构成,因此每个码字可表示k=log,2n比 特的输入信息。码的最小距离d=n/2。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 12 S = RHT =[0 0 0 0 1 0 1] 111 110 101 011 100 010 001 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ =[1 0 1] (8-3-22) 从表 8-3-3 中找到与 S=(110)相对应的错误图样(陪集首)为(001000),于是译码输出为 C =(0000101)+(001000)=(0010101) (8-3-23) 纠正了错误,译码正确。 若相同的码字经传输得 R =(1000101),其错误图样为 E’=(1010000),伴随式为 S= (011),由表 8-3-3 求得 E=(0001000) (8-3-24) 这时Cˆ =(1000101)+(0001000)=(1001101)≠C,译码是错误的,原因是 E’不是标准阵列的陪集 首。究其原因这种(7,4)码的 d min = 3,它可纠正任何一位差错,而不能纠正两位差错。 总之,线性码正确译码的充要条件是信道实际错误图样是标准阵列的陪集首,这个结 论对任何线性分组码的译码方法都适用。 8.3.5 一些特殊的线性分组码 (1)汉明码 汉明码有二进制的,也有非二进制的。二进制汉明码的共同特性是( , ) (2 1, 2 1) m m nk m = − −− , m 是校验位数,可取大于 1 任意整数。这些码的最小码间距离为 3。伴随式译码特别适合于 汉明码。例如 m =3,则得(7,4)汉明码,如前述例子;其最小码距 min d = 3 ,即最多可纠正 1 位错码。汉明码如果再加上一位对所有码元都进行校验的监督位,则监督码元由 m 增至 m + 1,信息位不变,码长由 2m – 1 增至 2m,通常把这种(2m,2m – 1 – m)码称为扩展汉明码。 扩展汉明码的最小码距增加为 4,能纠正 l 位错误同时检测 2 位错误。 (2) Hadamard 码 哈达马矩阵 Mn 是一个由“0”和“1”构成的 n n × 矩阵,构造方法如下: N=2 时, 2 0 0 0 1 M ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ , 2 2 4 2 2 M M M M M ⎡ ⎤ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ,依此类推, 2 n n n n n M M M M M ⎡ ⎤ = ⎢ ⎥ ⎢⎣ ⎥⎦ 。 哈达马矩阵每行就是一个 Walsh 序列,Hadamard 码可成对选取 n Mn M 的行向量,构成 码长为 n 的(, ) n k 线性分组码,该码由 2 n 个码字组构成,因此每个码字可表示 2 k n = log 2 比 特的输入信息。码的最小距离 min d n = / 2
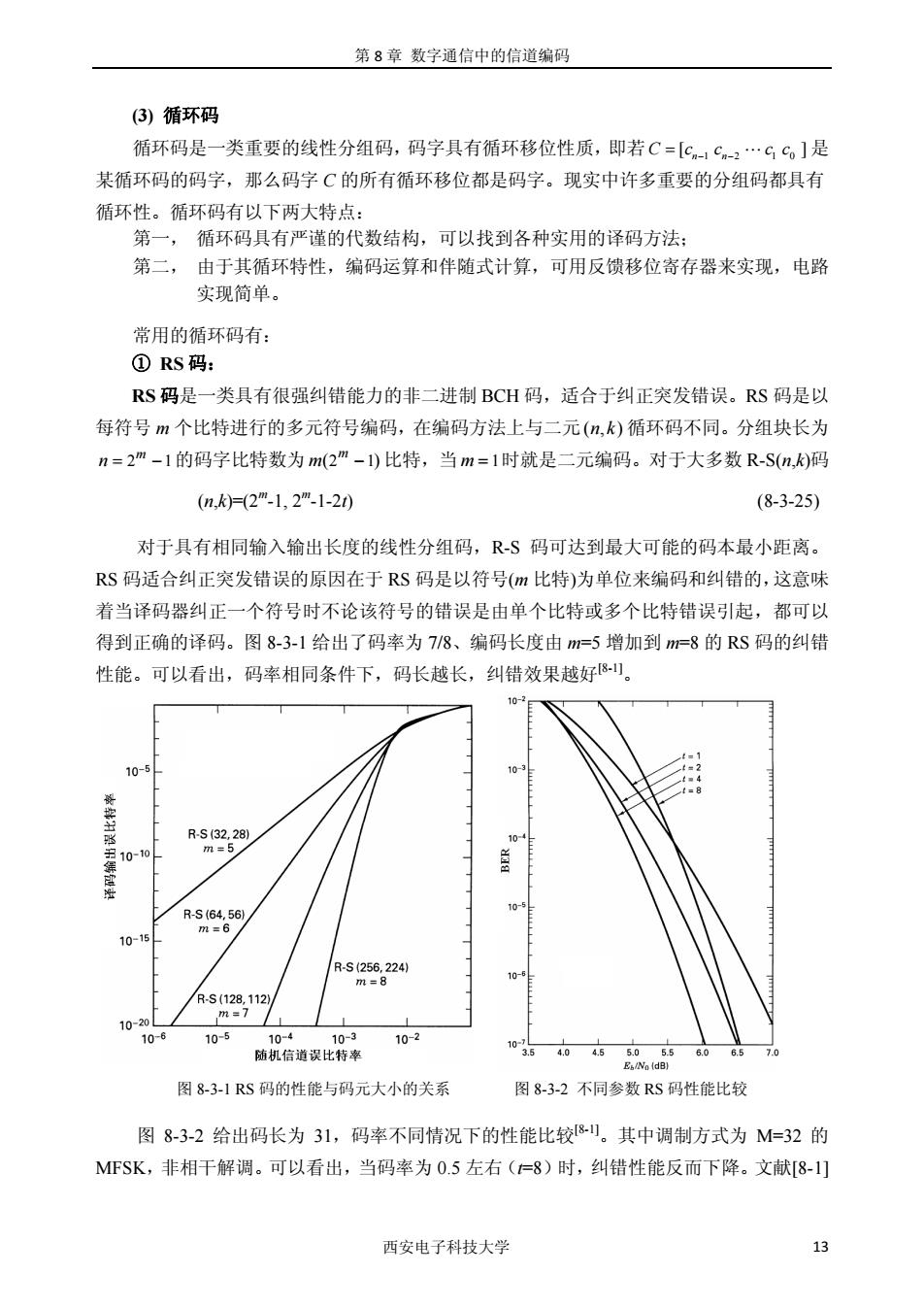
第8章数字通信中的信道编码 (仔)循环码 循环码是一类重要的线性分组码,码字具有循环移位性质,即若C=[c,.G,]是 某循环码的码字,那么码字C的所有循环移位都是码字。现实中许多重要的分组码都具有 循环性。循环码有以下两大特点: 第一,循环码具有严谨的代数结构,可以找到各种实用的译码方法: 第二,由于其循环特性,编码运算和伴随式计算,可用反馈移位寄存器来实现,电路 实现简单 常用的循环码有: ①RS码: RS码是一类具有很强纠错能力的非二进制BCH码,适合于纠正突发错误。RS码是以 每符号m个比特进行的多元符号编码,在编码方法上与二元(m,)循环码不同。分组块长为 n=2m-1的码字比特数为m(2m-)比特,当m=1时就是二元编码。对于大多数R-S(,k)码 (0n,k=2m-1,2m-1-20) (8-3-25) 对于具有相同输入输出长度的线性分组码,R-S码可达到最大可能的码本最小距离。 RS码适合纠正突发错误的原因在于RS码是以符号(m比特)为单位来编码和纠错的,这意味 着当译码器纠正一个符号时不论该符号的错误是由单个比特或多个比特错误引起,都可以 得到正确的译码。图8-3-1给出了码率为7/8、编码长度由m=5增加到m=8的RS码的纠错 性能。可以看出,码率相同条件下,码长越长,纠错效果越好。 10- -5 R5322 10-10 R5656 10- /Rs2562 752,12 10-20 10-5 防机信道误比特率 10-2 7. 图8-31RS码的性能与码元大小的关系 图8-3-2不同参数RS码性能比较 图8-3-2给出码长为31,码率不同情况下的性能比较8。其中调制方式为M=32的 MFSK,非相干解调。可以看出,当码率为0.5左右(=8)时,纠错性能反而下降。文献[8] 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 13 (3) 循环码 循环码是一类重要的线性分组码,码字具有循环移位性质,即若 1 2 10 [ ] C c c cc = n n − − " 是 某循环码的码字,那么码字 C 的所有循环移位都是码字。现实中许多重要的分组码都具有 循环性。循环码有以下两大特点: 第一, 循环码具有严谨的代数结构,可以找到各种实用的译码方法; 第二, 由于其循环特性,编码运算和伴随式计算,可用反馈移位寄存器来实现,电路 实现简单。 常用的循环码有: ① RS 码: RS 码是一类具有很强纠错能力的非二进制 BCH 码,适合于纠正突发错误。RS 码是以 每符号 m 个比特进行的多元符号编码,在编码方法上与二元(,) n k 循环码不同。分组块长为 2 1 m n = − 的码字比特数为 ( ) 2 1 m m − 比特,当 m =1时就是二元编码。对于大多数 R-S(n,k)码 (n,k)=(2m-1, 2m-1-2t) (8-3-25) 对于具有相同输入输出长度的线性分组码,R-S 码可达到最大可能的码本最小距离。 RS 码适合纠正突发错误的原因在于 RS 码是以符号(m 比特)为单位来编码和纠错的,这意味 着当译码器纠正一个符号时不论该符号的错误是由单个比特或多个比特错误引起,都可以 得到正确的译码。图 8-3-1 给出了码率为 7/8、编码长度由 m=5 增加到 m=8 的 RS 码的纠错 性能。可以看出,码率相同条件下,码长越长,纠错效果越好[8-1]。 图 8-3-1 RS 码的性能与码元大小的关系 图 8-3-2 不同参数 RS 码性能比较 图 8-3-2 给出码长为 31,码率不同情况下的性能比较[8-1]。其中调制方式为 M=32 的 MFSK,非相干解调。可以看出,当码率为 0.5 左右(t=8)时,纠错性能反而下降。文献[8-1]

第8章数字通信中的信道编码 给出了RS码在不同信道,BPSK调制下对应的最佳码率,其中AWGN信道最佳码率为 0.6~0.7,莱斯衰落信道最佳码率为0.5(对应莱斯因子为7),瑞利衰落信道最佳码率为0.3。 ②BCH码 >BCH码是循环码中功能强大的一类码,可以纠正多个随机错误,其参数可以在较大范 围内选用,适用性强,属于汉明码的推广。 >对于任何正数m(m心3)、(12m-1),存在一个长度为2m1的二进制BCH码,其最小距 离最少为2+1,最多有m个校验比特。 >当码长达到数百时,BCH码的性能超过了绝大部分相同码长和码率的其它分组码。对 于给定的码率,分组长度越长纠错性能越好。 >当码长大于8时长码硬判决的性能都会超过同码率n长短码的软判决性能。 汉明82 10 0 11 E/N(B) 图83-3BPSK相干解调经编码后的性能改善 图834不同分组码性能比较 8.4低密度奇偶校验码(LDPC码) ■LDPC码是一类特殊的线性分组码,其校验矩阵H绝大多数元素为0,非零元素1 的个数占总元素个数的比例非常小,即H是稀疏的,所以称之为低密度奇偶校验码。 ■这种特殊结构的校验矩阵使得LDPC码的译码复杂度及最小距离都随码长线性增 长。LDPC同经典分组码的最大不同在于如何译码。经典分组码通常是基于最大似 然(ML)算法译码的,这限制了码的长度,而LDPC是基于图形表示校验矩阵(即 Tanner图)的迭代译码,因此H矩阵的设计是关键。 ■LDPC码是一种可以逼近香农限的码,采用码率为12,最好的LDPC码字与香农限 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 14 给出了 RS 码在不同信道,BPSK 调制下对应的最佳码率,其中 AWGN 信道最佳码率为 0.6~0.7,莱斯衰落信道最佳码率为 0.5(对应莱斯因子为 7),瑞利衰落信道最佳码率为 0.3。 ②BCH 码 ¾ BCH 码是循环码中功能强大的一类码,可以纠正多个随机错误,其参数可以在较大范 围内选用,适用性强,属于汉明码的推广。 ¾ 对于任何正数 m(m≥3)、t(t<2m-1),存在一个长度为 2m-1 的二进制 BCH 码,其最小距 离最少为 2t+1,最多有 mt 个校验比特。 ¾ 当码长达到数百时,BCH 码的性能超过了绝大部分相同码长和码率的其它分组码。对 于给定的码率,分组长度越长纠错性能越好。 ¾ 当码长大于 8n 时长码硬判决的性能都会超过同码率 n 长短码的软判决性能。 图 8-3-3 BPSK 相干解调经编码后的性能改善 图 8-3-4 不同分组码性能比较 8.4 低密度奇偶校验码(LDPC 码) LDPC 码是一类特殊的线性分组码,其校验矩阵 H 绝大多数元素为 0,非零元素 1 的个数占总元素个数的比例非常小,即 H 是稀疏的,所以称之为低密度奇偶校验码。 这种特殊结构的校验矩阵使得 LDPC 码的译码复杂度及最小距离都随码长线性增 长。LDPC 同经典分组码的最大不同在于如何译码。经典分组码通常是基于最大似 然(ML)算法译码的,这限制了码的长度,而 LDPC 是基于图形表示校验矩阵(即 Tanner 图)的迭代译码,因此 H 矩阵的设计是关键。 LDPC 码是一种可以逼近香农限的码,采用码率为 1/2,最好的 LDPC 码字与香农限

第8章数字通信中的信道编码 的差距仅为0.0045dB,而采用码长为107,最大迭代译码次数为2000的仿真结果表 明,在106误码率下,与香农限的差距为0.04dB。 8.4.1LDPC码的表示方法 ()矩阵表示 与所有的线性分组码一样,LDPC码可以由校验矩阵来描述。图(8-4-1)给出了(20,3,4) 码的矩阵表示。 行数:J(15) 列数:n(20) 固定列权重:y(3) 固定行权重:p(4) 0000000100010001000 密度:=pn=小<1(1/5) 码率:R=kn2n-J)h=l-p 0000100001000010000 图8-41(20,3.4LDPC码 LDPC码字分为规则码和非规则码两种,它们相对应的校验矩阵称为正则矩阵和非正则矩 一个规则的LDPC码可以用(N,1,))来描述,其中N表示码长。校验矩阵H中每列含有1个 1,每行含有了个1。也就是说,每个编码比特会参与i个校验方程,而每个校验方程含有) 个绵编码的比特。 如果H的每列或者每行的非零元素的数目不完全相同,则所得到的码称为非规则LDPC码。 2)LDPC码的图形表示 ①LDPC码的Tanner图表示 >Tanner图不仅可以用图形来表示一线性分组码,而且有助于描述译码算法。对一个码 长为N、行数为K的校验矩阵H确定的线性分组码,可以用一个Tanner图来表示码 字比特和校验比特之间的关系。 >图84-2有两层顶点:第一层由K个校验节点顶点{C组成,对应着校验矩阵H的K 行;第二层则是由N个变量节点V组成,对应着校验矩阵H的N列。 >当且仅当h,1校验节点C,和变量节点V间相连,称之为“边”(edge),代表该变量节点 参与了与之相连的校验方程,即它们之间有数据信息的传递。 >在Tanner图上,与节点相连的边的个数叫做“度"(degree)。这样(N,i,j)规则LDPC码 的Tanner图中有N=K个“边”,每个变量节点的度为i,每个校验节点的度为j。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 15 的差距仅为 0.0045dB,而采用码长为 107 ,最大迭代译码次数为 2000 的仿真结果表 明,在 10-6误码率下,与香农限的差距为 0.04dB。 8.4.1 LDPC 码的表示方法 (1) 矩阵表示 与所有的线性分组码一样,LDPC 码可以由校验矩阵来描述。图(8-4-1)给出了(20,3,4) 码的矩阵表示。 图 8-4-1 (20,3,4)LDPC 码 LDPC 码字分为规则码和非规则码两种,它们相对应的校验矩阵称为正则矩阵和非正则矩 阵。 一个规则的 LDPC 码可以用(N, i , j )来描述,其中 N 表示码长。校验矩阵 H 中每列含有i 个 1,每行含有 j 个 1。也就是说,每个编码比特会参与i 个校验方程,而每个校验方程含有 j 个编码的比特。 如果 H 的每列或者每行的非零元素的数目不完全相同,则所得到的码称为非规则 LDPC 码。 (2) LDPC 码的图形表示 ① LDPC 码的 Tanner 图表示 ¾ Tanner 图不仅可以用图形来表示一线性分组码,而且有助于描述译码算法。对一个码 长为 N、行数为 K 的校验矩阵 H 确定的线性分组码,可以用一个 Tanner 图来表示码 字比特和校验比特之间的关系。 ¾ 图 8-4-2 有两层顶点:第一层由 K 个校验节点顶点{Ci}组成,对应着校验矩阵 H 的 K 行;第二层则是由 N 个变量节点{Vj}组成,对应着校验矩阵 H 的 N 列。 ¾ 当且仅当 hij=1 校验节点 Ci和变量节点 Vj间相连,称之为“边”(edge),代表该变量节点 参与了与之相连的校验方程,即它们之间有数据信息的传递。 ¾ 在 Tanner 图上,与节点相连的边的个数叫做“度”(degree)。这样(N, i , j )规则 LDPC 码 的 Tanner 图中有 Ni=Kj 个“边”, 每个变量节点的度为i ,每个校验节点的度为 j 。 行数:J (15) 列数:n (20) 固定列权重:γ (3) 固定行权重:ρ (4) 密度:r=ρ/n=γ/J<<1 (1/5) 码率:R=k/n≥(n-J)/n=1-γ/ρ