
■(一)格子设计的类别 ■平方格子设计(squared lattice):供试品种数为区 组内品种数的平方,区组内品种数为P,供试品种 数为p2; ■立方格子设计(cubic lattice):供试品种数为区组 内品种数的立方,区组内品种数为”,供试品种数 为p3; ·矩形格子设计:区组内品种数为P,供试品种数为 pp+1)
◼ (一) 格子设计的类别 ◼ 平方格子设计(squared lattice ):供试品种数为区 组内品种数的平方,区组内品种数为p,供试品种 数为p2; ◼ 立方格子设计(cubic lattice ):供试品种数为区组 内品种数的立方,区组内品种数为p,供试品种数 为p3; ◼ 矩形格子设计:区组内品种数为p,供试品种数为 p(p+1)

■(二)平方格子设计 ■1.仿照随机区组式的设计按品种分组方法的变换次 数有: ■(1)简单格子设计(simple lattice)品种分组方法为二 种,试验重复次数为2或2的倍数。 重复I 重复Ⅲ (1) 123 (4) 147 区组 (2) 456 (5) 258 (3) 789 (6) 369
◼ (二) 平方格子设计 ◼ 1. 仿照随机区组式的设计 按品种分组方法的变换次 数有: ◼ (1) 简单格子设计(simple lattice)品种分组方法为二 种,试验重复次数为2或2的倍数。 重复 I 重复Ⅱ (1) 1 2 3 (4) 1 4 7 区组 (2) 4 5 6 (5) 2 5 8 (3) 7 8 9 (6) 3 6 9

■(2)三重格子设计(triple lattice):品种分组方法为三 种,即在简单格子设计二种分组方法的基础上再增 加对角线分组一种,重复次数为3或3的倍数。 重复I 重复Ⅲ 重复Ⅲ (1) 123 (4) 147 (7)159 区组 (2) 456 (5)258 (8)267 (3)789 (6)369 (9)348 ■(3)四重格子设计(quadruple lattice):在三重格子设 计的基础上,再增加对角线一组
◼ (2) 三重格子设计(triple lattice):品种分组方法为三 种,即在简单格子设计二种分组方法的基础上再增 加对角线分组一种,重复次数为3或3的倍数。 ◼ (3) 四重格子设计(quadruple lattice):在三重格子设 计的基础上,再增加对角线一组, 重复 I 重复Ⅱ 重复 III (1) 1 2 3 (4) 1 4 7 (7) 1 5 9 区组 (2) 4 5 6 (5) 2 5 8 (8) 2 6 7 (3) 7 8 9 (6) 3 6 9 (9) 3 4 8
分组法X 分组法Y 分组法Z 分组法L 161116 171319 181517 区组 (1)12345 (6) 21 (11) 25 (16) 24 271217 281420 291118 (2) 678910 (7) 22 (12) 21 (17) 25 11121314 381318 391516 3101219 (3) 15 (8) 23 (13) 22 (18) 21 16171819 491419 4101117 461320 (4) 20 (9) 24 (14) 23 (19) 22 21222324 5101520 561218 571416 (5) 25 (10) 25 (15) 24 (20) 23 5×5四重格子设计方法 ■(4)平衡格子设计(balanced lattice):品种分组方法 增加到使每一对品种都能在同一区组中相遇一次
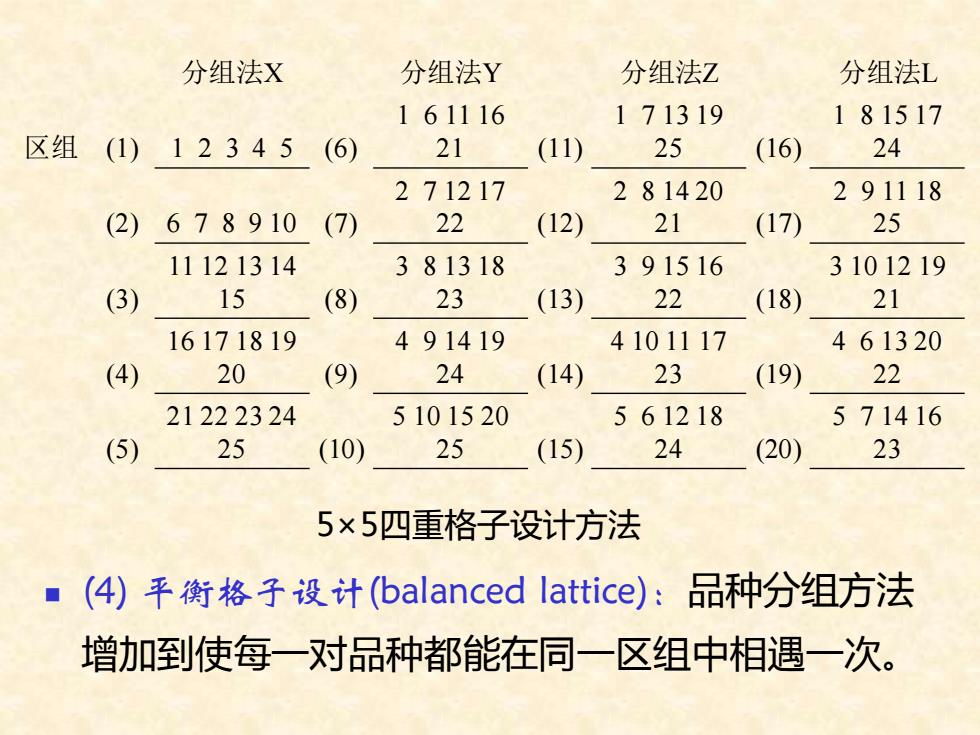
◼ (4) 平衡格子设计(balanced lattice):品种分组方法 增加到使每一对品种都能在同一区组中相遇一次。 分组法X 分组法Y 分组法Z 分组法L 区组 (1) 1 2 3 4 5 (6) 1 6 11 16 21 (11) 1 7 13 19 25 (16) 1 8 15 17 24 (2) 6 7 8 9 10 (7) 2 7 12 17 22 (12) 2 8 14 20 21 (17) 2 9 11 18 25 (3) 11 12 13 14 15 (8) 3 8 13 18 23 (13) 3 9 15 16 22 (18) 3 10 12 19 21 (4) 16 17 18 19 20 (9) 4 9 14 19 24 (14) 4 10 11 17 23 (19) 4 6 13 20 22 (5) 21 22 23 24 25 (10) 5 10 15 20 25 (15) 5 6 12 18 24 (20) 5 7 14 16 23 5×5四重格子设计方法

重复 重复 重复 重复 I IⅡ IV (1)123 (4)147 (7)159 (10) 168 区 组 (2)456 (5)258 (8)267 (11) 249 (3)789 (6)369 (9)348(12)357 3×3平衡格子设计 ■2.仿照拉丁方的格子设计 ■(①)平衡格子方设计(balanced lattice square) ■①重复数=(p+1)/2,每对品种在行或列区组中共相 遇一次;
◼ 2. 仿照拉丁方的格子设计 ◼ (1) 平衡格子方设计(balanced lattice square) ◼ ①重复数r=(p+1)/2,每对品种在行或列区组中共相 遇一次; 重复 Ⅰ 重复 Ⅱ 重复 Ⅲ 重复 Ⅳ (1) 1 2 3 (4) 1 4 7 (7) 1 5 9 (10) 1 6 8 区 组 (2) 4 5 6 (5) 2 5 8 (8) 2 6 7 (11) 2 4 9 (3) 7 8 9 (6) 3 6 9 (9) 3 4 8 (12) 3 5 7 3×3平衡格子设计