
第七章卡平方(x2)测验 第一节卡平方(x)的定义和分布 第二节在方差同质性测验中的应用 第三节适合性测验 第四节独立性测验 第五节X的可加性和联合分析
第七章 卡平方( )测验 2 第一节 卡平方( )的定义和分布 第二节 在方差同质性测验中的应用 第三节 适合性测验 第四节 独立性测验 第五节 的可加性和联合分析 2 2 2

第一节卡平方(X)的定义和分布 所谓X,是指相互独立的多个正态离差平方值的总和, 即 -听+时t.听心。月 (71) 其中,y服从正态分布N(4,o),4,=(y,-4)/o 为标准正态离差
第一节 卡平方( )的定义和分布 2 2 所谓 ,是指相互独立的多个正态离差平方值的总和, 即: − = + + + + + = = i i i i i i n i y u u u u u 2 2 2 2 2 2 2 1 2 ( ) (7·1) 其中,yi 服从正态分布 , 为标准正态离差。 ( , ) 2 N i i i i i i u = (y − )/

y不一定来自同一个正态总体,即4,及σ,可以是不 同正态分布的参数。若通常所研究的对象属同一个总体, 则4,=4,0:=0,从而 =。4 (72)
yi不一定来自同一个正态总体,即 及 可以是不 同正态分布的参数。若通常所研究的对象属同一个总体, 则 , ,从而 i i i = i = 2 2 − = i i y (7·2)

之抽样分布的密度函数为/0X)=Xe1 22T(v/2) X2累积分布函数为 F(x2)=P(x2≥x)=∫f(x2)d(x2) X分布的自由度为独立的正态离差的个数,此处v=n ,其分布图形为一组具不同自由度v值的曲线(图7.1)。 X值最小为0,最大为+∞,因而在坐标轴的右面。 自由度小时呈偏态,随着自由度增加,偏度降低,至+∞ 时,呈对称分布。 该分布的平均数为v,方差为2v
2 抽样分布的密度函数为 2 ( 2) ( ) ( ) 2 2 ( 2) 1 2 2 2 Γ ν / χ e f χ ν/ ν/ − − χ = 累积分布函数为 2 ( ) ( ) ( ) ( ) 2 2 2 2 2 2 F P f d p p = p = + 分布的自由度为独立的正态离差的个数,此处 v =n ,其分布图形为一组具不同自由度 v 值的曲线(图7.1)。 值最小为0,最大为+∞,因而在坐标轴的右面。 自由度小时呈偏态,随着自由度增加,偏度降低,至+∞ 时,呈对称分布。 该分布的平均数为 v ,方差为2v。 2 2
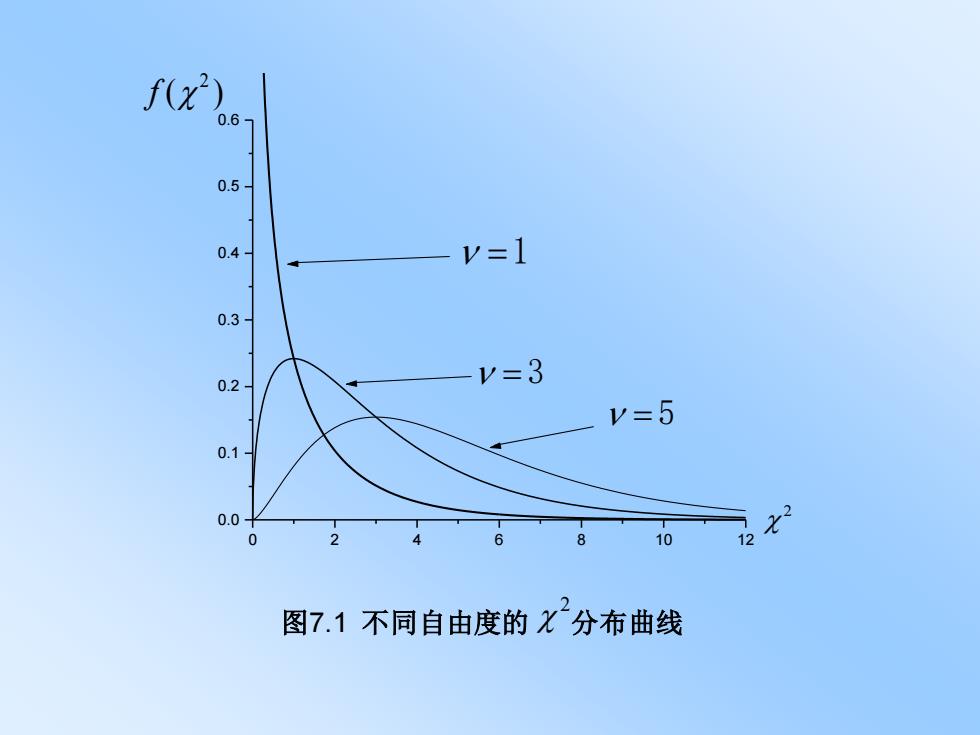
f(x 0.6 0.5 0.4 y=1 0.3 0.2 y=3 y=5 0.1 0.0 0 10 图7.1不同自由度的X分布曲线
0 2 4 6 8 10 12 0.0 0.1 0.2 0.3 0.4 0.5 0.6 ( ) 2 f 图7.1 不同自由度的 分布曲线 2 =1 = 3 = 5 2