
第六章方差分析 第一节方差分析的基本原理 第二节多重比较 第三节方差分析的线性模型与期望均方 第四节单向分组资料的方差分析 第五节两向分组资料的方差分析 第六节方差分析的基本假定和数据转换
第六章 方差分析 第一节 方差分析的基本原理 第二节 多重比较 第三节 方差分析的线性模型与期望均方 第四节 单向分组资料的方差分析 第五节 两向分组资料的方差分析 第六节 方差分析的基本假定和数据转换

第一节方差分析的基本原理 方差是平方和除以自由度的商。 所谓方差分析(analysis of variance),是关于k(k23)个样本 平均数的假设测验方法,是将总变异剖分为各个变异来源的 相应部分,从而发现各变异原因在总变异中相对重要程度的 一种统计分析方法。 假设测验的依据是:扣除了各种试验原因所引起的 变异后的剩余变异提供了试验误差的无偏估计。 这里采用均方来度量试验处理产生的变异和误差引起的 变异
第一节 方差分析的基本原理 所谓方差分析(analysis of variance) ,是关于k(k≥3)个样本 平均数的假设测验方法,是将总变异剖分为各个变异来源的 相应部分,从而发现各变异原因在总变异中相对重要程度的 一种统计分析方法。 假设测验的依据是:扣除了各种试验原因所引起的 变异后的剩余变异提供了试验误差的无偏估计 。 这里采用均方来度量试验处理产生的变异和误差引起的 变异. 方差是平方和除以自由度的商
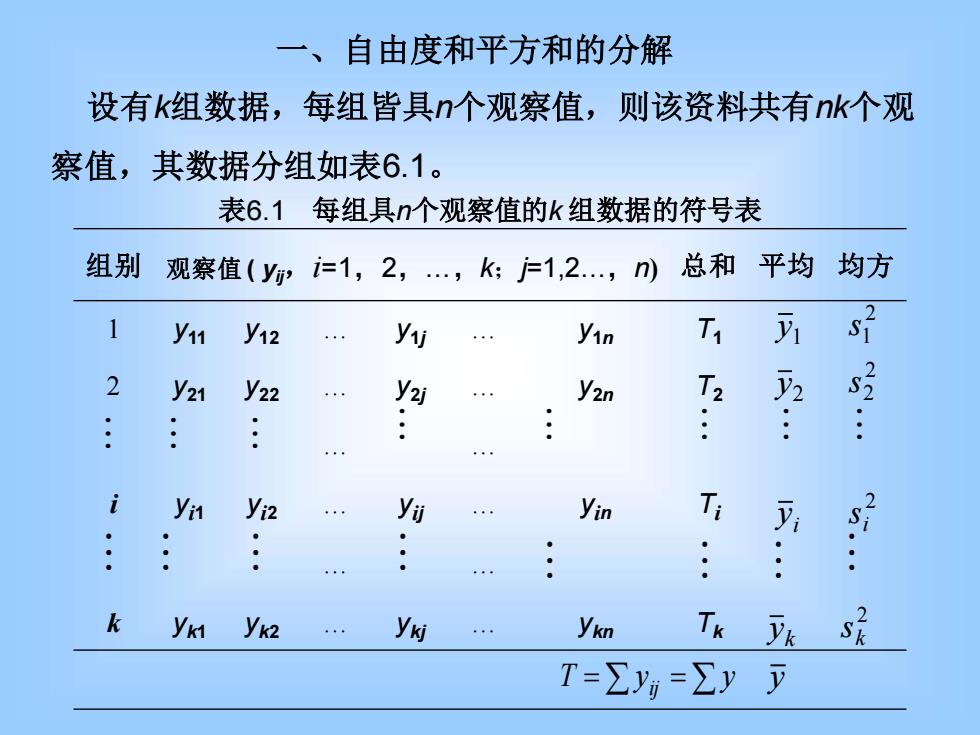
一、自由度和平方和的分解 设有k组数据,每组皆具n个观察值,则该资料共有nk个观 察值,其数据分组如表6.1。 表6.1每组具n个观察值的k组数据的符号表 组别 观察值(y? i1,2,.,k:j=1,2.,n总和 平均均方 y11 y12 y . yin T 1 s 2 y21 y22 y2j y2n T2 2 : i Vn Vi2 y闭 yin Ti 。 : k yk yk2 y yk知 Tk k T=∑y=∑y
一、自由度和平方和的分解 设有k组数据,每组皆具n个观察值,则该资料共有nk个观 察值,其数据分组如表6.1。 表6.1 每组具n个观察值的k 组数据的符号表 组别 观察值 ( yij,i=1,2,.,k;j=1,2.,n) 总和 平均 均方 1 y11 y12 . y1j . y1n T1 2 y21 y22 . y2j . y2n T2 . . i yi1 yi2 . yij . yin Ti . . k yk1 yk2 . ykj . ykn Tk T = y = y ij 1 y 2 y i y k y y 2 1 s 2 2 s 2 i s 2 k s

在表6.1中,总变异是nk个观察值的变异,故其自由度 v=nk一1,而其平方和SS则为: 5S,=克0y,-列2=空听-C (61) 其中的C称为矫正数: C=②以2T2 (62) nk nk 对于第i组的变异,有 三0,-=2,-男+g-列 20-+220-+20-明 =2,-)广+0-
在表6.1中,总变异是nk个观察值的变异,故其自由度 v = nk-1,而其平方和SST则为: = − = − n k n k SST yi j y yi j C 1 1 2 2 ( ) (6·1) 其中的C称为矫正数: nk T nk y C 2 2 = = ( ) (6·2) 对于第 i 组的变异,有 2 1 2 1 2 1 1 2 1 2 1 2 ( ) ( ) ( ) 2( )( ) ( ) ( ) ( ) y y n y y y y y y y y y y y y y y y y i n j i j i n j i n j i j i i n j i j i n j i j i i n j i j = − + − = − + − − + − − = − + − = = = = = =

从而总变异(61)可以剖分为: sS,0-=0,+2-列 (63) 即 总平方和=组内(误差)平方和+处理平方和 组间变异由k个的变异引起,故其自由度=k一1,组 间平方和SS为: s8,=吃-2=r2n-C (64) 组内变异为各组内观察值与组平均数的变异,故每组具有 自由度v=n一1和平方和2(y,-,)2;而资料共有k组,故组 内自由度v=k(n一1),组内平方和SS。为: SS。=2[(y,-,)2]=SSr-SS, (65)
从而总变异(6·1)可以剖分为: = − = − + − = = = = = k i i k i n j i j i k i n j T i j SS y y y y n y y 1 2 1 1 2 1 1 2 ( ) ( ) ( ) (6·3) 即 总平方和=组内(误差)平方和+处理平方和 组间变异由k个 的变异引起,故其自由度 v =k-1 , 组 间平方和 SSt 为: i y = − = − k k SSt n yi y Ti n C 1 1 2 2 ( ) 组内变异为各组内观察值与组平均数的变异,故每组具有 自由度 v =n-1和平方和 ;而资料共有k 组,故组 内自由度 v = k (n-1) ,组内平方和 SSe 为: − n ij i y y 1 2 ( ) = − = − k n e i j i SST SSt SS y y 1 1 2 [ ( ) ] (6·5) (6·4)