复旦大学：《微电子学与固体电子学》教学资源（博士士学位论文）高精度、低功耗流水线型模数转换器的研究与设计

第二章模数转换器概述 THD=10lg Total Harmonic Distortion Power (2.7) Signal Power 计算式为 2 2 THD=20lg (2.8) Aintrms) (e)有效位(Effective Number of Bits,ENOB) ENOB表示有效位，由于与分辨率具有相同的单位，因此可以直观地表示 ADC所能达到的有效精度，有 ENOB= SINADdB.Fs-1.76dB (2.9) 6.02 其中SINADdB,Fs是满幅信号输入下得到的值。 2.2.3性能系数 在实际应用中，模数转换器有着不同的精度、转换速度和功耗，为了在各种 不同ADC中进行比较，可以通过性能系数(Figure-of-merit,,FOM)来定义，最被 广泛采用的性能系数定义为 FOM= 2EoB×f (2.10) 其中P为功耗，ENOB是有效位，而fs是最大采样频率。FOM的单位是pJ/step。 FOM越小表示模数转换器的性能越好。 2.3模数转换器测试原理 ADC的测试有各种不同的方法1-5]，为了得到一种普遍被接受的测试方法， IEEE组织制定了一系列有关模数转换器的测试标准，如IEEE STD1057和IEEE 1241等。下面对模数转换器的测试原理进行分析。 2.3.1动态参数测试 由于现实中产生的所有信号中，正弦波所能达到的信号纯度是最高的，因此 对于ADC而言，可以采用正弦波作为信号的输入。通常采用的测试平台架构如 图2.4所示。 13

第二章 模数转换器概述 13 10lg Total Harmonic Distortion Power THD Signal Power        (2.7) 计算式为 22 2 2[ ] 3[ ] [ ] [ ] 20lg HD rms HD rms HDN rms in rms AA A THD A           (2.8) (e) 有效位 (Effective Number of Bits，ENOB) ENOB 表示有效位，由于与分辨率具有相同的单位，因此可以直观地表示 ADC 所能达到的有效精度，有 , 1.76 6.02 SINAD dB dB FS ENOB   (2.9) 其中 SINADdB,FS是满幅信号输入下得到的值。 2.2.3 性能系数 在实际应用中，模数转换器有着不同的精度、转换速度和功耗，为了在各种 不同 ADC 中进行比较，可以通过性能系数(Figure-of-merit，FOM)来定义，最被 广泛采用的性能系数定义为 2ENOB s P FOM f   (2.10) 其中 P 为功耗，ENOB 是有效位，而 fs 是最大采样频率。FOM 的单位是 pJ/step。 FOM 越小表示模数转换器的性能越好。 2.3 模数转换器测试原理 ADC 的测试有各种不同的方法[1-5]，为了得到一种普遍被接受的测试方法， IEEE组织制定了一系列有关模数转换器的测试标准，如IEEE STD 1057和IEEE 1241 等。下面对模数转换器的测试原理进行分析。 2.3.1 动态参数测试 由于现实中产生的所有信号中，正弦波所能达到的信号纯度是最高的，因此 对于 ADC 而言，可以采用正弦波作为信号的输入。通常采用的测试平台架构如 图 2.4 所示

高精度、低功耗流水线型模数转换器的研究与设计 Clock Sine wave BP Filter Analog Input ADC Digital out Logic (DUT) Analyzer Sine wave BP Filter FFT 图2.4ADC测试平台 信号发生器产生正弦波，经过带通滤波器后输入进待测ADC,同时时钟信 号也可以由信号发生器得到。其数字输出通过逻辑分析仪进行采样并且保存，之 后对保存的结果进行FFT分析，根据FFT分析的结果，便可以得到SINAD、 SFDR、THD和SNR等各种动态特性。FFT分析和动态特性的计算通常由电脑 程序来完成。 值得注意的是，根据快速傅里叶变换的性质，需要仔细地设置输入信号的频 率以避免发生频谱泄露，因此需要根据ADC采样频率和采样点的个数来设置输 入信号，输入信号应当满足式(2.11)的要求，其中N为采样的点数，M一般为一 个小于N2的质数。若是在欠采样条件下，M则应当大于N2。 五-M f N (2.11) 信号的幅度为应当接近满幅，但是通常为了防止信号过载，也可以略小于满 幅，如-1dBFS。 2.3.2静态参数测试 静态参数的仿真可以用斜波，考察从+VR到-VR线性变化的输入信号对应的 数字码输出。一般在1LSB量程应当取到10到20个数字码。而在实际测试中 可以采用“码密度法”，即采用经过适当滤波的正弦波输入信号，采集足够长时 间的数字输出，考察各个码出现的次数，再将各个码值出现的次数进行统计并绘 制图表。 在理论上，先采用三角波来进行分析。以分辨率为10bit为例，当输入略微 过载的三角波时，由于信号过载，需要略去全0和全1的码值即0和1023，统 计出1到1022各码出现的总次数M,同时得到各码理论上应当出现的次数 14

高精度、低功耗流水线型模数转换器的研究与设计 14 图 2.4 ADC 测试平台 信号发生器产生正弦波，经过带通滤波器后输入进待测 ADC，同时时钟信 号也可以由信号发生器得到。其数字输出通过逻辑分析仪进行采样并且保存，之 后对保存的结果进行 FFT 分析，根据 FFT 分析的结果，便可以得到 SINAD、 SFDR、THD 和 SNR 等各种动态特性。FFT 分析和动态特性的计算通常由电脑 程序来完成。 值得注意的是，根据快速傅里叶变换的性质，需要仔细地设置输入信号的频 率以避免发生频谱泄露，因此需要根据 ADC 采样频率和采样点的个数来设置输 入信号，输入信号应当满足式(2.11)的要求，其中 N 为采样的点数，M 一般为一 个小于 N/2 的质数。若是在欠采样条件下，M 则应当大于 N/2。 in s f M f N  (2.11) 信号的幅度为应当接近满幅，但是通常为了防止信号过载，也可以略小于满 幅，如-1dB FS。 2.3.2 静态参数测试 静态参数的仿真可以用斜波，考察从+VR 到-VR 线性变化的输入信号对应的 数字码输出。一般在 1LSB 量程应当取到 10 到 20 个数字码。而在实际测试中 可以采用“码密度法”，即采用经过适当滤波的正弦波输入信号，采集足够长时 间的数字输出，考察各个码出现的次数，再将各个码值出现的次数进行统计并绘 制图表。 在理论上，先采用三角波来进行分析。以分辨率为 10bit 为例，当输入略微 过载的三角波时，由于信号过载，需要略去全 0 和全 1 的码值即 0 和 1023，统 计出 1 到 1022 各码出现的总次数 MT，同时得到各码理论上应当出现的次数 hT

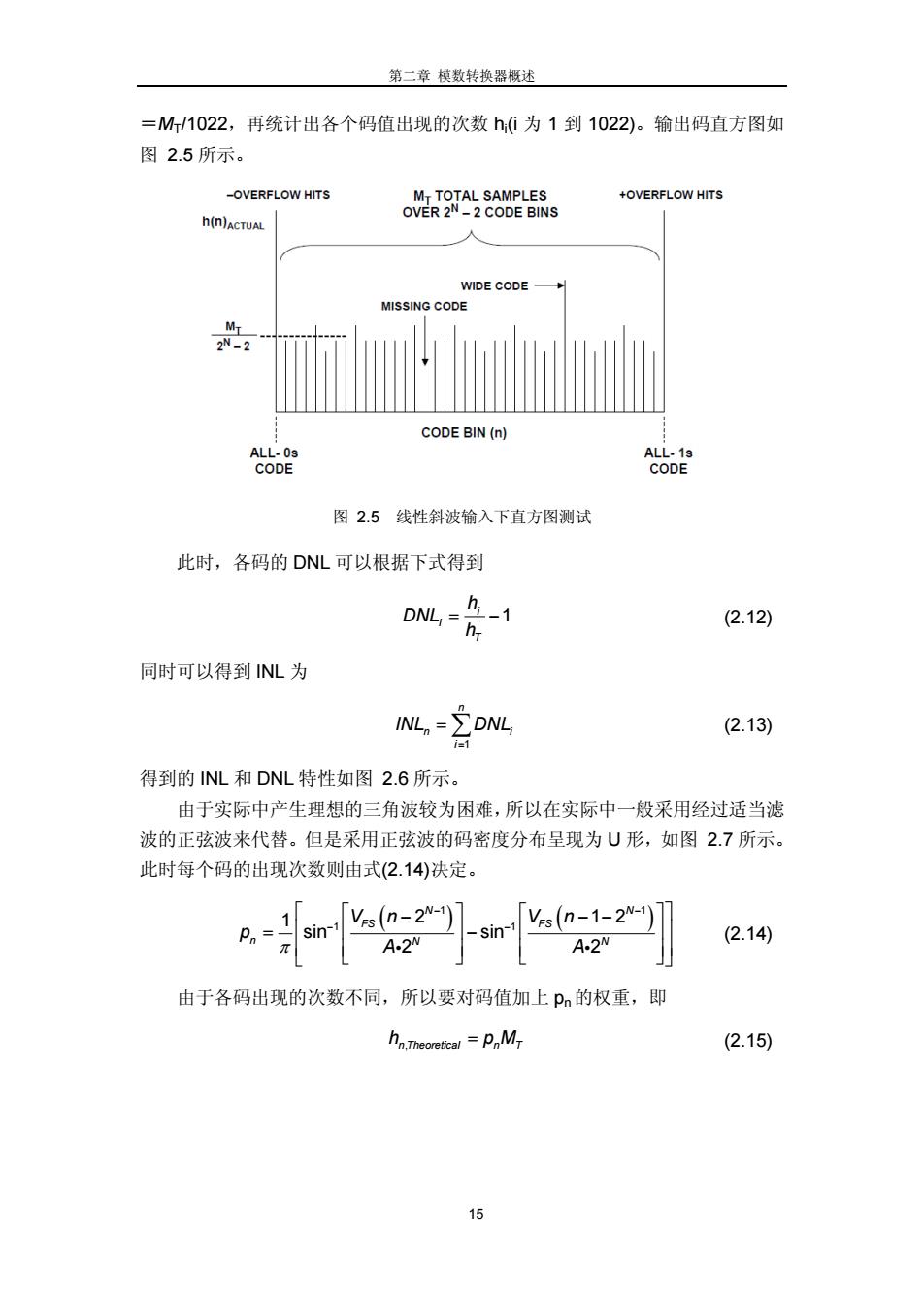
第二章模数转换器概述 =M/1022,再统计出各个码值出现的次数h(1为1到1022)。输出码直方图如 图2.5所示。 -OVERFLOW HITS MT TOTAL SAMPLES +OVERFLOW HITS h(n)ACTUAL OVER 2N-2 CODE BINS WIDE CODE MISSING CODE 2N-2 CODE BIN(n) ALL-0s ALL-1s CODE CODE 图2.5线性斜波输入下直方图测试 此时，各码的DNL可以根据下式得到 DNL= h1 (2.12) h 同时可以得到NL为 INL,=DNL (2.13) 得到的INL和DNL特性如图2.6所示。 由于实际中产生理想的三角波较为困难，所以在实际中一般采用经过适当滤 波的正弦波来代替。但是采用正弦波的码密度分布呈现为U形，如图2.7所示。 此时每个码的出现次数则由式(2.14)决定。 a-r2"mra2] (2.14) 由于各码出现的次数不同，所以要对码值加上p的权重，即 hn.Theoretical =PnM (2.15) 15

第二章 模数转换器概述 15 ＝MT/1022，再统计出各个码值出现的次数 hi(i 为 1 到 1022)。输出码直方图如 图 2.5 所示。 图 2.5 线性斜波输入下直方图测试 此时，各码的 DNL 可以根据下式得到 1 i i T h DNL h   (2.12) 同时可以得到 INL 为 1 n n i i INL DNL    (2.13) 得到的 INL 和 DNL 特性如图 2.6 所示。 由于实际中产生理想的三角波较为困难，所以在实际中一般采用经过适当滤 波的正弦波来代替。但是采用正弦波的码密度分布呈现为 U 形，如图 2.7 所示。 此时每个码的出现次数则由式(2.14)决定。     1 1 1 1 1 2 12 sin sin 2 2 N N FS FS n N N Vn Vn p  A A                          (2.14) 由于各码出现的次数不同，所以要对码值加上 pn的权重，即 h pM n Theoretical n T ,  (2.15)

高精度、低功耗流水线型模数转换器的研究与设计 +0.5 DNL 0 -0.5 00.00 11..11 +2.0 n +1.5 INLn=∑DNL; i=0 +1.0 +0.5 INL 0 -0.5 -1.0+ 图2.6DNL和INL示意 Vin)=Asin2πt ADC INPUT RANGE=±VFS p(n) n- 1 2N1 2N-2 图2.7正弦波输入下码密度测试 16

高精度、低功耗流水线型模数转换器的研究与设计 16 图 2.6 DNL 和 INL 示意 图 2.7 正弦波输入下码密度测试

第二章模数转换器概述 从而有 DNL= n.ActuaL1 (2.16) P M 为了得到精确的结果，有几点需要注意：第一，输入的正弦波频率不应是采 样频率的亚谐波：第二，正弦波的幅值可以稍微过载：第三，需要仔细调节正弦 波的偏移以消除电路的直流偏移，从而获得对称的码输出：最后，正弦波的幅值 可以根据直方图结果，由下式计算得到 A= VEs M, (2.17） sin M+ho+hw1 2 此幅值可以代入式(2.14)计算得到各码出现次数。 此外，这种方法还可以测试ADC的等效输入噪声。为此，可以把输入接适 当电阻，再加直流电压，记录一定量的输出码。这样，等效输出噪声就会表现为 以对应码附近一定范围内的码值输出。假设噪声是高斯分布的，则可以根据峰峰 噪声输出码直方图得到等效均方根噪声，如图28所示。 P-P INPUT NOISE NUMBER OF OCCURRENCES ≈6.6×RMS NOISE 一 o=RMS NOISE(LSBs) 图 n-4 n-3m-2n-1nn+1n+2n+3n+4 OUTPUT CODE 图2.8采用直方图法测试ADC噪声 按照上述方法，通过逻辑分析仪采集到一定数量的输出码后，可以用Matlab 程序进行处理，直接得到结果。 2.4模数转换器的分类 第一款单片集成的模数转换器产生于20世纪70年代，当时基本上是以全 并行快闪(Flash)结构6-11]和折叠型结构12-20]为主。进入80年代之后，在低 速高分辨率ADC中，逐次逼近型结构模数转换器(SAR,Successive 17

第二章 模数转换器概述 17 从而有 , 1 n Actual n n T h DNL p M   (2.16) 为了得到精确的结果，有几点需要注意：第一，输入的正弦波频率不应是采 样频率的亚谐波；第二，正弦波的幅值可以稍微过载；第三，需要仔细调节正弦 波的偏移以消除电路的直流偏移，从而获得对称的码输出；最后，正弦波的幅值 可以根据直方图结果，由下式计算得到 0 2 1 sin N 2 FS T T V A M Mhh             (2.17) 此幅值可以代入式(2.14)计算得到各码出现次数。 此外，这种方法还可以测试 ADC 的等效输入噪声。为此，可以把输入接适 当电阻，再加直流电压，记录一定量的输出码。这样，等效输出噪声就会表现为 以对应码附近一定范围内的码值输出。假设噪声是高斯分布的，则可以根据峰峰 噪声输出码直方图得到等效均方根噪声，如图 2.8 所示。 图 2.8 采用直方图法测试 ADC 噪声 按照上述方法，通过逻辑分析仪采集到一定数量的输出码后，可以用 Matlab 程序进行处理，直接得到结果。 2.4 模数转换器的分类 第一款单片集成的模数转换器产生于 20 世纪 70 年代，当时基本上是以全 并行快闪(Flash)结构[6-11]和折叠型结构[12-20]为主。进入 80 年代之后，在低 速高分辨率 ADC 中，逐次逼近型结构模数转换器 (SAR ， Successive