
共轭复数的运算性质 06士=乙±;a2)=;(色4)= 72 (2) Z=3 (3)zz=x2+y=(Rez)+(Imz) (4)z+z=2Re(z) =2i lm()
共轭复数的运算性质 ( ) ( ) ; 1 1 2 1 2 z z = z z ( ) ; 1 2 1 2 z z = z z 2 1 2 1 ( ) z z z z = (2) z = z 2 Im( ) (4) 2Re( ) z z i z z z z − = + = ( ) ( ) ( ) 2 2 2 2 3 zz = x + y = Re z + Im z

例1.1 设两复数21=x1+y1,22=x2+y2, 证明乙1·z2+元1z2=2R(z1z2), 证 12+Z1Z2= (x1+y1)x2-y2)+(x1-y1)(x2+y2) =(x12+y1y2)+i(x2Jy1-x1y2) +(xx2+V2)+ix2+xV2) =2(x1X2+Jy1y2)=2R(z1·z2). 或1·2+2=1·2+12=2R(12)
12 例1.1 证 , , 1 1 1 2 2 2 设两复数 z = x +iy z = x +iy 2Re( ). 1 2 1 2 1 2 证明 z z + z z = z z z1 z2 + z1 z2 = ( )( ) ( )( ) 1 1 2 2 1 1 2 2 x + iy x − iy + x − iy x + iy ( ) ( ) 1 2 1 2 2 1 1 2 = x x + y y + i x y − x y ( ) ( ) 1 2 1 2 2 1 1 2 + x x + y y + i −x y + x y 2( ) 1 2 1 2 = x x + y y 2Re( ). 1 2 = z z 2Re( ). 1 2 1 2 1 2 1 2 1 2 或 z z + z z = z z + z z = z z
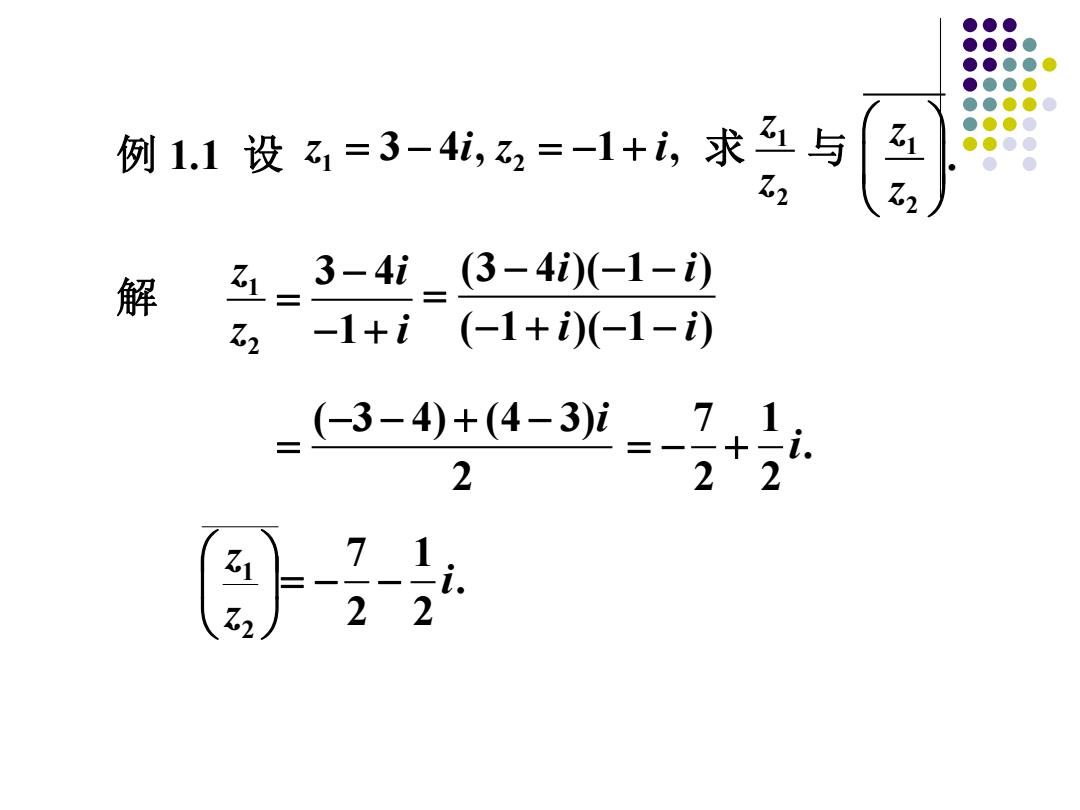
例1.1设1=3-4,2=-1+i,求与 Z2 五初 3-4i (3-4i)(-1-i) 解 乙1 乙2 -1+i (-1+)(-1-) (-3-4)+(4-3) 2 =+ 7 1
解 12 3 4 1 z i z i − = − + (3 4 )( 1 ) ( 1 )( 1 ) i i i i − − − = − + − − ( 3 4) (4 3) 2 − − + − i = 7 1 . 2 2 = − + i 21 zz 7 1 . 2 2 = − − i 例 1.1 设 1 2 z i z i = − = − + 3 4 , 1 , 12 zz 求 与 12 . zz

例1.2 i=i, 4n=1, 2=-1, iantl=i, 3=i2=-i, 4+2=-1, 计=2.2=1, i4n+3=-i, i4n+4=1
例 1.2 1 i i = , 2 i = −1, 3 2 i i i i = = − , 4 2 2 i i i = = 1, …… 1, 4 = n i , 4 1 i i n = + 1, 4 2 = − n+ i 4 3 , n i i + = − 4 4 1. n i + =
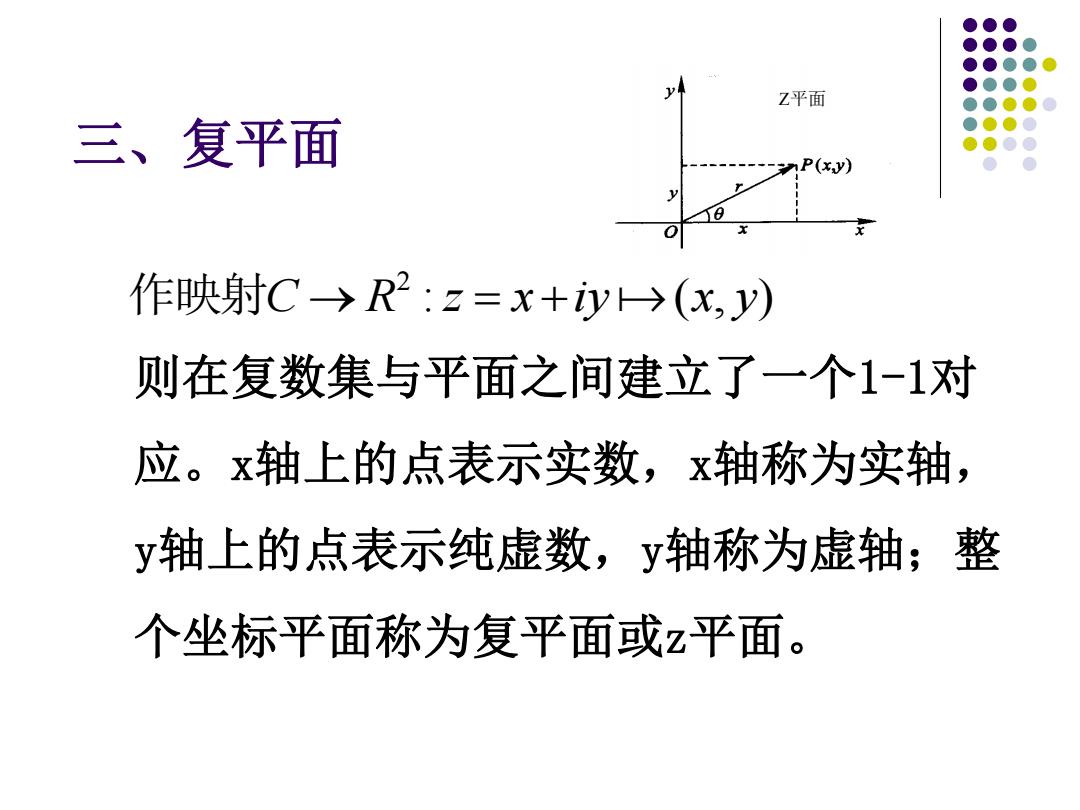
Z平面 三、复平面 P(xy) 作映射C→R2:z=x+iy→(x,y) 则在复数集与平面之间建立了一个1-1对 应。x轴上的点表示实数,x轴称为实轴, y轴上的点表示纯虚数,y轴称为虚轴;整 个坐标平面称为复平面或z平面
三、复平面 则在复数集与平面之间建立了一个1-1对 应。x轴上的点表示实数,x轴称为实轴, y轴上的点表示纯虚数,y轴称为虚轴;整 个坐标平面称为复平面或z平面。 : ( , ) 2 作映射C → R z = x +iy x y Z平面