
§1.2复数的三角表示 (The representation of complex number) 一 复数的模和辐角 复数的三角不等式 三、 复数的表示方法 四、 用复数的三角表示作乘除法 五、复数的乘方与开方
§1.2 复数的三角表示 (The representation of complex number) 一、复数的模和辐角 二、复数的三角不等式 三、复数的表示方法 四、用复数的三角表示作乘除法 五、复数的乘方与开方
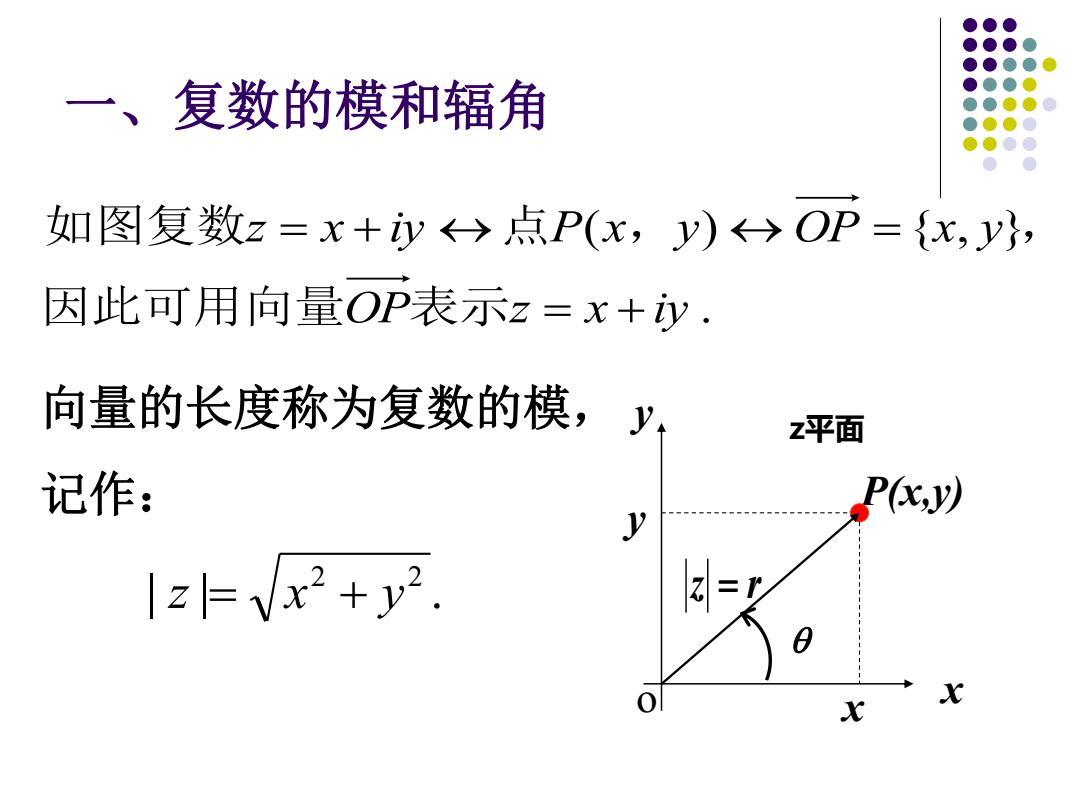
一、复数的模和辐角 如图复数z=x+y→点P(x,y)←>OP={x,y}, 因此可用向量OP表示z=x+y. 向量的长度称为复数的模,y, z平面 记作: PK以 y lz=x2+y2 X X
一、复数的模和辐角 o x y z平面 P(x,y) z = r x y . ( ) { , } OP z x iy z x iy P x y OP x y = + = + = 因此可用向量 表示 如图复数 点 , , 向量的长度称为复数的模, 记作: | | . 2 2 z = x + y

向量与正实轴之间的夹角称为复数z 的辐角(Argument),记作:e=Arg. 由于任意非零复数有无限多个辐角, 用Argz表示符合 -z<arg条z 件的一个角,称为复数主辐角。于是 Argz=argz+2kπ k=0,±1,士2,… 注意:z=0时,辐角不确定
向量与正实轴之间的夹角称为复数 的辐角(Argument),记作: 由于任意非零复数有无限多个辐角, 用 表示符合 条 件的一个角,称为复数主辐角。于是 = Argz. − arg z Argz Argz = arg z + 2k k = 0,1, 2, 注意: z = 0 时,辐角不确定。 z

下面给出argz与arctan'之间的关系 X arctan',当x>0,y≥0, X π 2 当x=0,y>0, arctan Y+π,当x<0,y≥0, X 其中-至aretm T arg -2 2≠0 arctan y-π,当x<0,y<0, X X π 21 当x=0,y<0, arctan',当x>0,y<0:
下面给出 与 之间的关系 x y arg z arctan 2 arctan 2 − x y 其 中 − = − + = = arctan , 0, 0; , 0, 0; 2 arctan , 0, 0; arctan , 0, 0; , 0, 0; 2 arctan , 0, 0; arg 0 x y x y x y x y x y x y x y x y x y x y z z 当 当 当 当 当 当

例3求Arg(2-2)及Arg(-3+4i) 解Arg(2-2i)=arg(2-2i)+2kπ arctan 2 2k元 2 =2kx (k=0,±1,±2,) 4 Ag(-3+4)=arg(-3+40)+2kπ=-arctan3+2kr+元 =(2k+1)π-arctan 3 (k=0,±1,±2,…)
2 k 22 arctan + − = 2 ( 0, 1, 2, ) 4 = − + k k = Arg( − 3 + 4 i ) = arg( − 3 + 4 i ) + 2 k + + − = 2 k 34 arctan( 0, 1, 2, ) 34 = (2 k +1) − arctan k = 例3 求 Arg( ) 2 2 − i 及 Arg( ) − +3 4i 解 Arg( 2 − 2 i ) = arg( 2 − 2 i ) + 2 k