
只有输出支路的节点称为输入节点或源点7; 只有输入支路的节点称为输出节点或阱点8: 既有输入支路又有输出支路的节点叫做混合节点。 通路是指从源点到阱点之间沿着箭头方向的连续的 串支路,通路的增益是该通路上各支路增益的乘 积7-1-2-6-3-4-8。 回路是指从一个节点出发沿着支路箭头方向到达同一 个节点的闭合通路,它象征着系统中的反馈回路 3-4-5-6-3。组成回路的所有支路增益的乘积通常 叫做回路增益 。 每个节点可以同时含有几条输入支路和几条输出支路, 任一节点的信号变量值等于所有输入支路信号之 和
只有输出支路的节点称为输入节点或源点7; 只有输入支路的节点称为输出节点或阱点8; 既有输入支路又有输出支路的节点叫做混合节点。 通路是指从源点到阱点之间沿着箭头方向的连续的一 串支路,通路的增益是该通路上各支路增益的乘 积7-1-2-6-3-4-8。 回路是指从一个节点出发沿着支路箭头方向到达同一 个节点的闭合通路,它象征着系统中的反馈回路 3-4-5-6-3。组成回路的所有支路增益的乘积通常 叫做回路增益。 每个节点可以同时含有几条输入支路和几条输出支路, 任一节点的信号变量值等于所有输入支路信号之 和

2、梅逊Mason)公式: 利用信号流图,可列出一线性方程组,求得系 统函数。利用信号流图中的梅逊公式,可以方 便地求得系统函数。梅逊公式如下 me-是-a 式中T为从输入节点(源点)到输出节点(阱 点)的第条前向通路增益;△为流图的特征式 A=1-∑L+∑LL,-∑LLyL… i. △是不接触第条前向通路的特征式余因子
2、梅逊(Mason)公式: 利用信号流图,可列出一线性方程组,求得系 统函数。利用信号流图中的梅逊公式,可以方 便地求得系统函数。梅逊公式如下 ( ) ( ) ( ) = = k Tk k X z Y z H z 1 式中Tk为从输入节点(源点)到输出节点(阱 点)的第k条前向通路增益; Δ为流图的特征式 = − + − i j k i j i j i Li L L L L L , ' ' 1 Δk是不接触第k条前向通路的特征式余因子

)L为所有不同回路增益之和 工工为每个互不接触回路增益之和, i,l 互不接触指两个回路之间无公共的支路或结点; ∑LL,L为每三个互不接触的回路增益之和; i,i,k △是第k条前向通路的特征式余因子 A=1-∑L,+∑L,L十. i./ 所有L,LL均是第k条通路不接触的回路
所有 均是第 条通路不接触的回路。 = + + 是第 条前向通路的特征式余因子 为每三个互不接触的回路增益之和; 互不接触指两个回路之间无公共的支路或结点; 为每个互不接触回路增益之和, 为所有不同回路增益之和 L L L k L L L k L L L L L L i i j j i j i i k i k k i j k i j j i j i i i ' ' ' , ' " , , " " ' , ' 1- .......
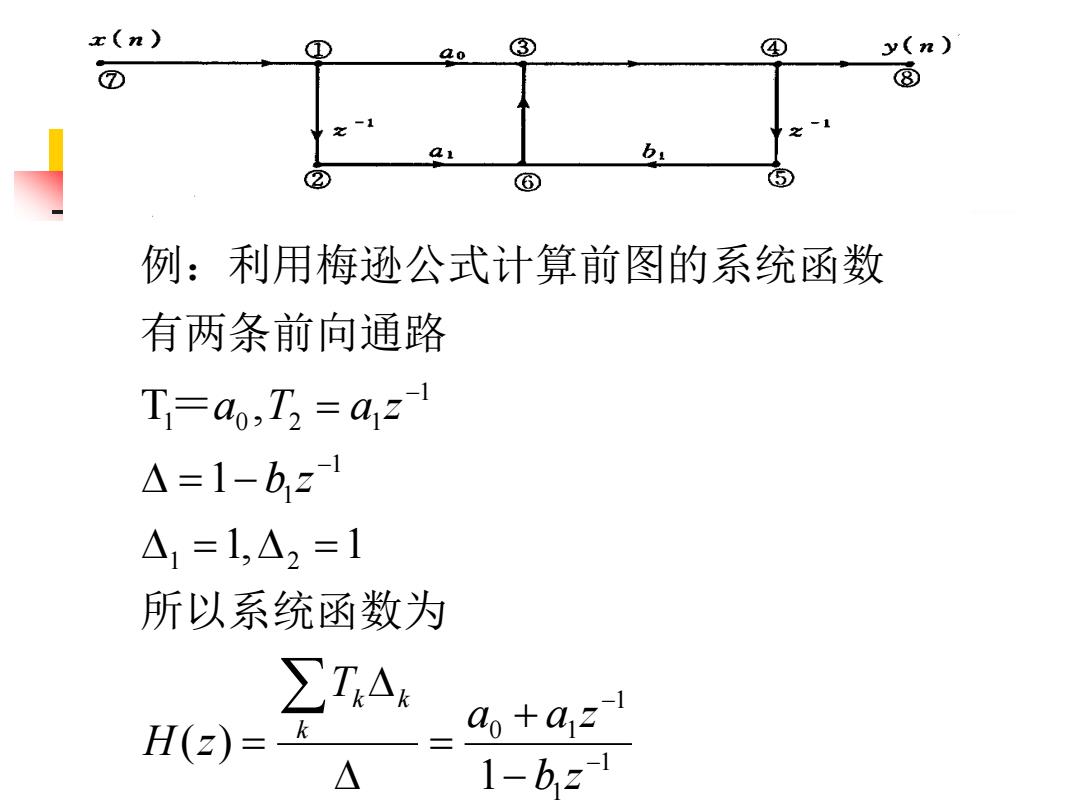
x(n) ① ao ③ ④ y(n) ⑦ ⑧ 之一1 2-1 ai ② ⑥ ⑤ 例:利用梅逊公式计算前图的系统函数 有两条前向通路 T=ao,T2 az △=1-b,21 △1=1,△2=1 所以系统函数为 ∑T△ H(z)= ao az 1-b2-1
1 1 1 0 1 1 2 1 1 1 1 0 2 1 1 ( ) 1, 1 1 T , − − − − − + = = = = = − = b z a a z T H z b z a T a z k k k 所以系统函数为 = 有两条前向通路 例:利用梅逊公式计算前图的系统函数

3、信号流图的转置定理: 对于单个输入、单个输出的系统,通过反 转网络中的全部支路的方向,并且将其输入 和输出互换,得出的流图具有与原始流图相 同的系统函数
对于单个输入、单个输出的系统,通过反 转网络中的全部支路的方向,并且将其输入 和输出互换,得出的流图具有与原始流图相 同的系统函数。 3、信号流图的转置定理: