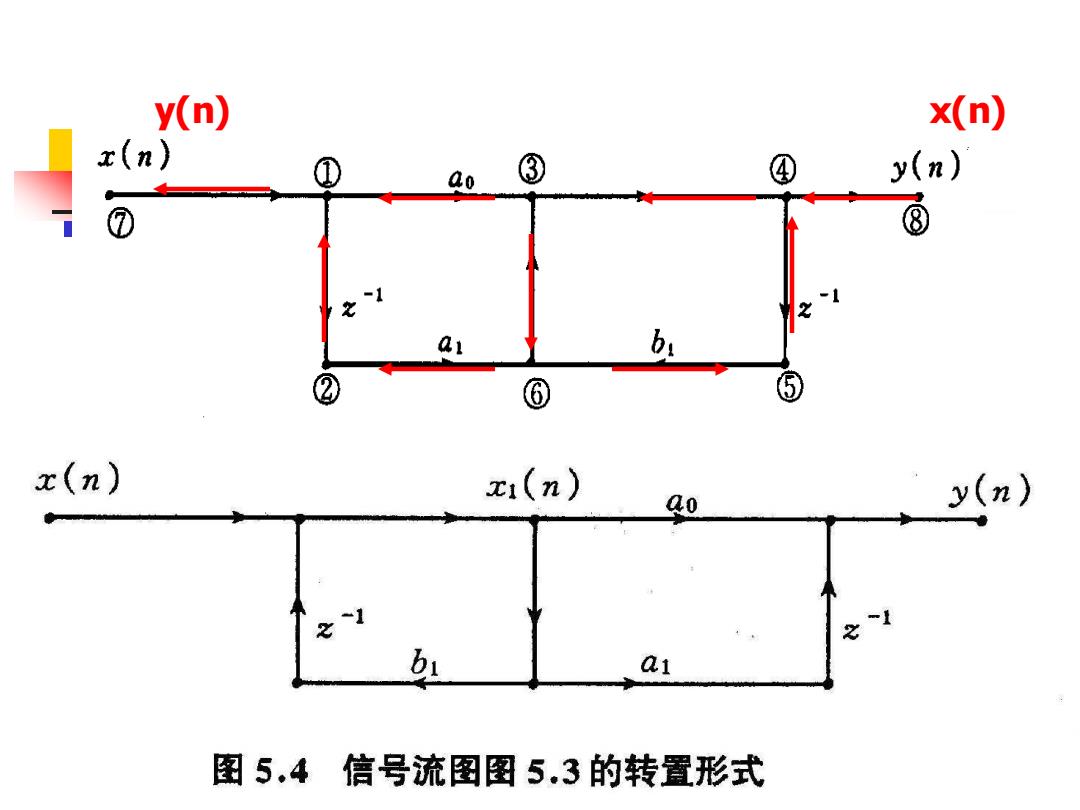
y(n) x(n) z(n) ① ao ③ ④ y(n) ⑦ ⑧ -1 -1 之 2 ai bi ② ⑥ x(n) x1(n) ao y(n)》 21 -1 图5.4 信号流图图5.3的转置形式
y(n) x(n)

信号流图转置的作用: ①转变运算结构; ②验证计算流图的系统函数的正确与否。 运算结构对滤波器的实现很重要,尤其对于一 些定点运算的处理机,结构的不同将会影响系统的 精度、误差、稳定性、经济性以及运算速度等许多 重要的性能。对于无限长单位冲激响应(IIR)数 字滤波器与FR数字滤波器,它们在结构上各有自己 不同的特点,因此我们在下面将对它们分别加以讨 论
信号流图转置的作用: ①转变运算结构; ②验证计算流图的系统函数的正确与否。 运算结构对滤波器的实现很重要,尤其对于一 些定点运算的处理机,结构的不同将会影响系统的 精度、误差、稳定性、经济性以及运算速度等许多 重要的性能。对于无限长单位冲激响应(I I R)数 字滤波器与FIR数字滤波器,它们在结构上各有自己 不同的特点,因此我们在下面将对它们分别加以讨 论

5.1.2R数字滤波器的结构 IIR DF特点 一个N阶RD有理的系统函数可能表示为: Y( H(z)= i=0 1->b,Z-1 X( 则这一系统差分方程为=1 y(m))=∑a,y(0n-)+之b,x(n-i) i=0 i=1
5.1.2 IIR数字滤波器的结构 一、IIR DF特点 一个N阶IIR DF有理的系统函数可能表示为: 则这一系统差分方程为: ( ) ( ) 1 ) 1 0 X z Y z b Z a Z H z N i i i M i i i = − = = − = − ( = = = − + − M i i N i i y n a y n i b x n i 0 1 ( ) ( ) ( )

根据前两式可见 1 单位冲激响应h(n)是无限长的n→o 2.系统函数H(z)在有限长Z平面(0<Z<oo) 有极点存在。 3.系统的输出不仅与现在和以前的输入有 关,而且还与以前的输出有关。结构上存 在输出到输入的反馈,也即结构上是递归 型的。 4.同一系统函数,有各种不同的结构形式
根据前两式可见 1.单位冲激响应h(n)是无限长的n→∞ 2.系统函数H(z)在有限长Z平面(0<|Z|<∞) 有极点存在。 3.系统的输出不仅与现在和以前的输入有 关,而且还与以前的输出有关。结构上存 在输出到输入的反馈,也即结构上是递归 型的。 4.同一系统函数,有各种不同的结构形式

(1)直接型 直接由RDF的差分方程所得的网 络结构。 (m)=∑a,xn-0+Σb(n-) i=0 方程看出:yn)电两部分组成: 第一部分∑二4,x(n一i)是一个对输入x) 的N节延时链结树。即每个延时后加权相加。 第二部分∑b,y(n一)是一个N节延时链结 构网络。不过它是对y(n)延时,因而是个反馈网络
(1) 直接型 直接由 IIR DF 的差分方程所得的网 络结构。 = = = − + − N i i N i i y n a x n i b y n i 0 1 ( ) ( ) ( ) 方程看出:y(n)由两部分组成: 第一部分 是一个对输入x(n) 的N节延时链结构。即每个延时后加权相加。 第二部分 是一个N节延时链结 构网络。不过它是对y(n)延时,因而是个反馈网络。 = − N i i b y n i 1 ( ) = − N i i a x n i 0 ( )