
对于上面的算式,可以化成不同的计算形式,如 苴接计算、分解为多个有理函数相加、分解为多个 理函数相乘等等,不同的计算形式也就表现出不 同的计算结构,而不同的计算结构可能会带来不同 的效果,或者是实现简单,编程方便,或者是计算 精度较高等等 另外,数字信号是通过采样和转换得到的,而 转换的位数是有限的(一般6、8、10、12、16位) ,所以存在量化误差,另外,计算机中的数的表示 也总是有限的,经此表示的滤波器的系数同样存在 量化误差,在计算过程中因有限字长也会造成误差
对于上面的算式,可以化成不同的计算形式,如 直接计算、分解为多个有理函数相加、分解为多个 有理函数相乘等等,不同的计算形式也就表现出不 同的计算结构,而不同的计算结构可能会带来不同 的效果,或者是实现简单,编程方便,或者是计算 精度较高等等。 另外,数字信号是通过采样和转换得到的,而 转换的位数是有限的(一般6、8、10、12、16位) ,所以存在量化误差,另外,计算机中的数的表示 也总是有限的,经此表示的滤波器的系数同样存在 量化误差,在计算过程中因有限字长也会造成误差

量化误差主要有三种误差: ①A/D变换量化效应; ②系数的量化效应; ③数字运算的有限字长效应
①A/D变换量化效应; ②系数的量化效应; ③数字运算的有限字长效应。 量化误差主要有三种误差:
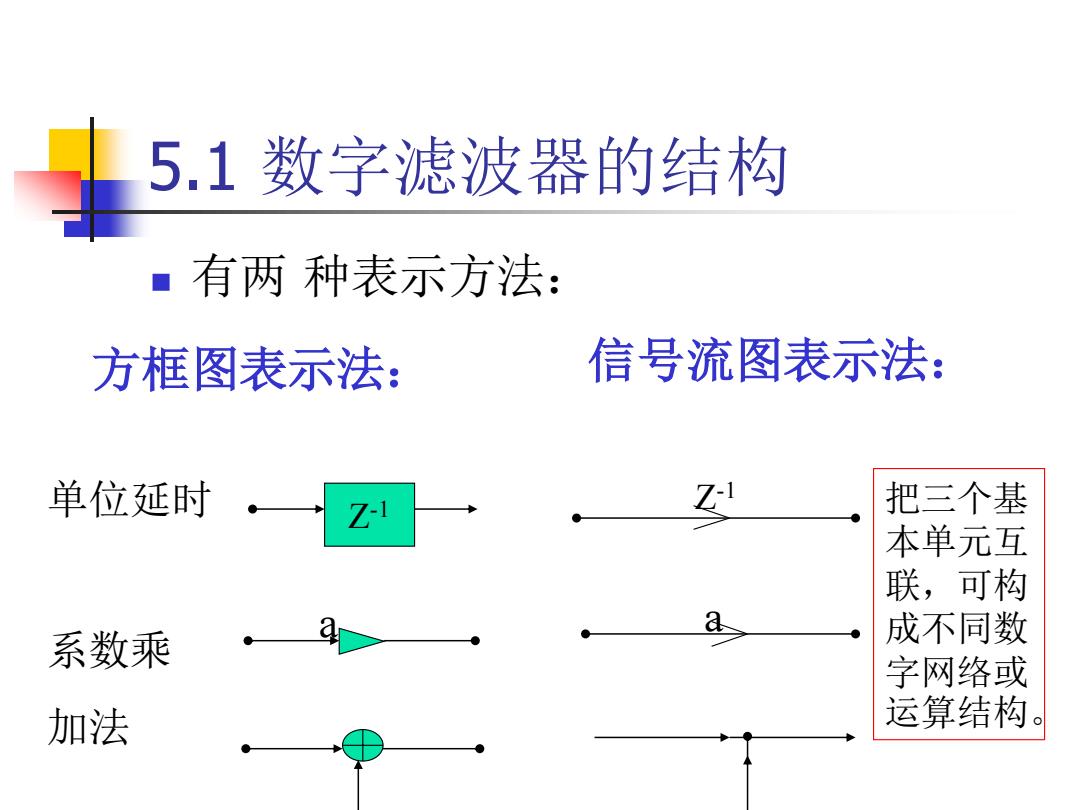
5.1数字滤波器的结构 有两种表示方法: 方框图表示法: 信号流图表示法: 单位延时。 Z Z-i 把三个基 本单元互 联,可构 系数乘 2 成不同数 字网络或 加法 运算结构
5.1 数字滤波器的结构 ◼ 有两 种表示方法: 方框图表示法: 信号流图表示法: Z 单位延时 -1 系数乘 加法 a 把三个基 本单元互 联,可构 成不同数 字网络或 运算结构。 Z -1 a
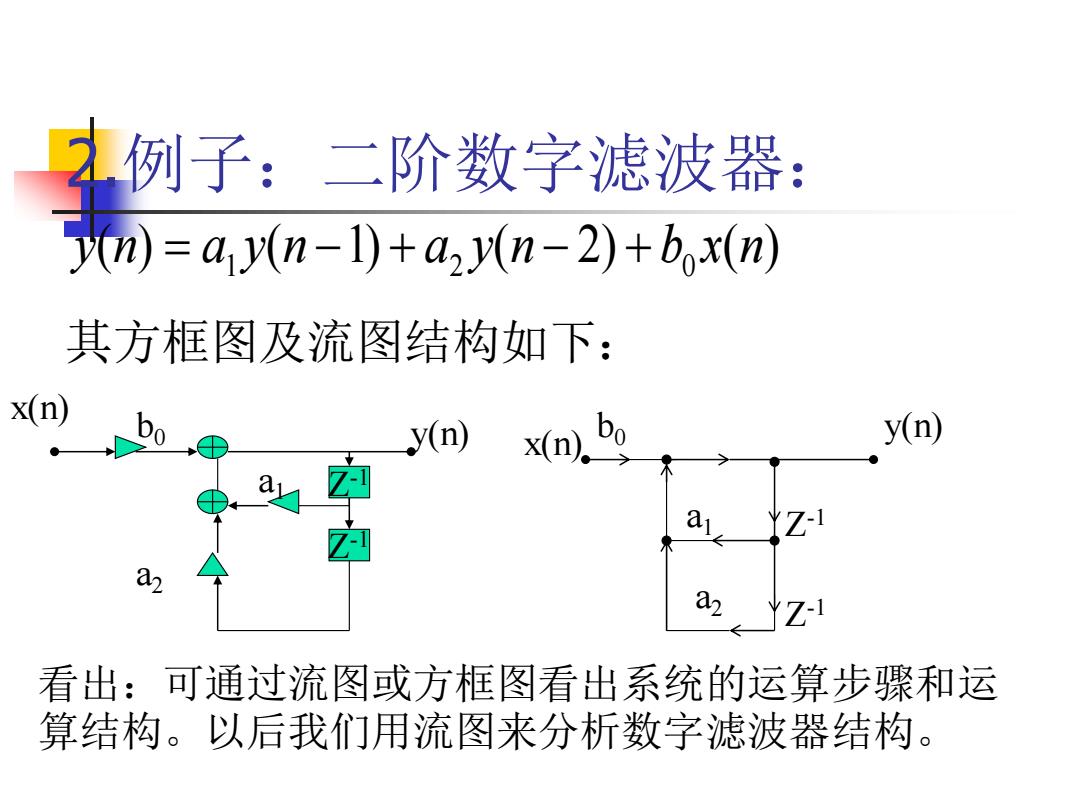
例子:二阶数字滤波器: m)=a(n-1)+a2(n-2)+bx(n) 其方框图及流图结构如下: x(n) bo y(n) x(n)bo y(n) a -1 看出:可通过流图或方框图看出系统的运算步骤和运 算结构。以后我们用流图来分析数字滤波器结构
2.例子:二阶数字滤波器: ( ) ( 1) ( 2) ( ) 1 2 0 y n = a y n − + a y n − + b x n 其方框图及流图结构如下: Z -1 Z -1 b0 y(n) a1 a2 看出:可通过流图或方框图看出系统的运算步骤和运 算结构。以后我们用流图来分析数字滤波器结构。 x(n) b y(n) 0 a1 a2 Z -1 Z -1 x(n)
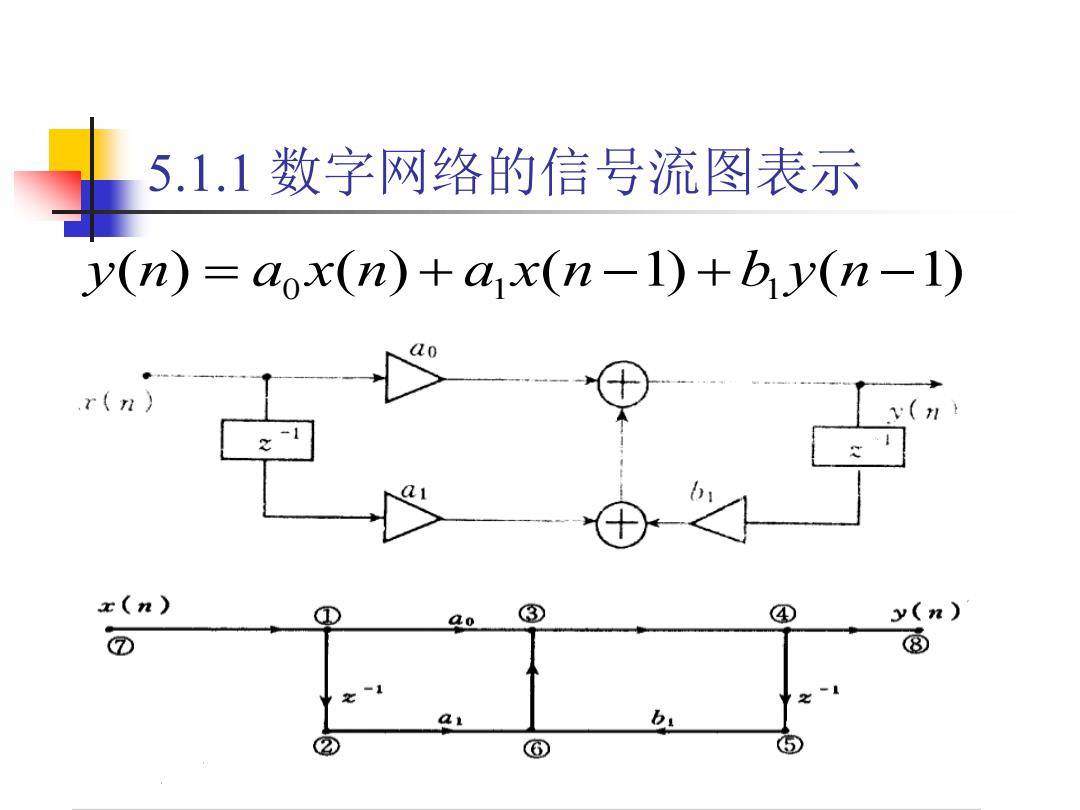
5.1.1数字网络的信号流图表示 y(n)=aox(n)+ax(n-1)+by(n-1) ao r(n x(n) ③ ④ y(n) ⑦ ⑧ 之1 2x a1 b ②④ ⑥ ⑤
5.1.1 数字网络的信号流图表示 ( ) ( ) ( 1) ( 1) y n = a0 x n + a1 x n − +b1 y n −