
1.2 判断x)=sm型)-c0)是否是周期序列?确定其周期的长度。 oa-号-41 T,T,的最小公倍数是该序列的周期T=56
1.2 T T T 56 14 T 14 2 7 ) 7 cos( 8 T 8 2 4 ) 4 sin( ) 7 ) cos( 4 ( ) sin( 1 2 2 0 0 1 0 0 , 的最小公倍数是该序列的周期 = , = , = , = ; , = , = , = ; 判断 是否是周期序列?确定其周期的长度。 n n n n x n = −

1.7 Z0.5"[u())-u(n-10l=∑0.5”z n=0 1-(0.5z1)10z10-0.510 1-0.5z1z9(z-0.5) 2*k 零点:z10=0.510,3k=0.5eo,k=0,110-1 极点:z=0(9阶)z=0.5 z=0.5处零极点抵消
1.7 ( 0.5) 0.5 1 0.5 1 (0.5 ) 0.5 [ ( ) ( 10)] 0.5 9 1 0 1 0 1 1 1 0 9 0 − − = − − = − − = − − = − z z z z z Z u n u n z n n n n 处零极点抵消 极点: ( 阶) 零点: 0.5 0 9 0.5 0.5 , 0.5 , 0,1,.......10 1 * 1 0 2 1 0 1 0 = = = = = = − z z z z z e k j k k
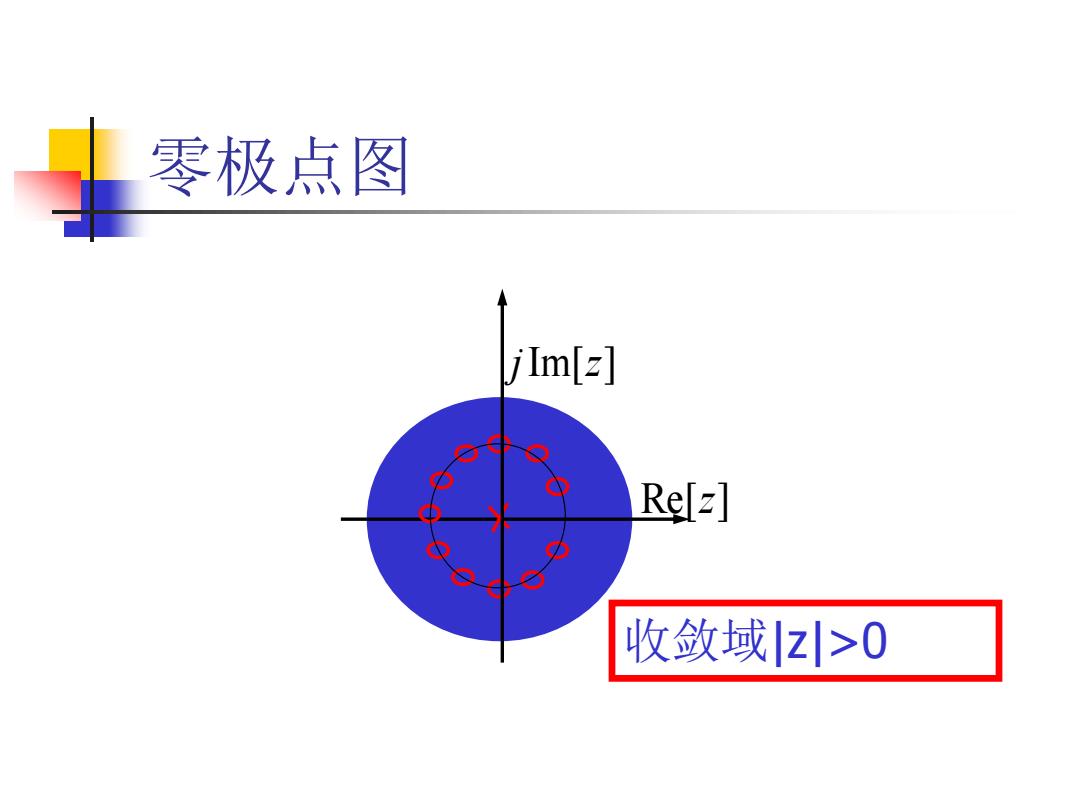
零极点图 jIm[z] Relz] 收敛域z>0
零极点图 Re[ ]z j z Im[ ] 收敛域|z|>0

1.13 (2) 解:设T[x(n)]=[x(n)]'T[x2n=[x,(n] :T[x(n)+x(n)]=[x(n)+x,(n)] =[x(n)]+[,(n)]+2x(n)x,(n) ≠T[x(n)]+T[x(n)] 不满足可加性 或T[ax(n)]=[a(n)订=a2[x(n)]≠ar[x(n)] 不满足比例性 不是线性系统 T[x(n-m)]=[x(n-m)=y(n-m)=[x(n-m) 是移不变系统
1.13 (2) ( ) ( ) ( ) ( ) 2 T x n x n x n x n 1 2 1 2 + = + 不满足可加性 或 ( ) ( ) 2 T ax n ax n = 不满足比例性 不是线性系统 ( ) ( ) 2 T x n m x n m − = − 是移不变系统( ) ( ) ( ) ( ) 2 2 1 2 1 2 = + + x n x n x n x n 2 + T x n T x n 1 2 ( ) ( ) 解:设 2 1 1 T x n x n ( ) ( ) = 2 2 2 T x n x n ( ) ( ) = ( ) ( ) 2 2 = a x n aT x n ( ) 2 = y n m x n m − = − ( )

1.13(3) 设y(n)=T[x,(n]=∑x(m), y,(n))=T[x2(ml=∑x,(m) 1m=-00 而T[ax,(m)+bx,n】=∑[ax,(m)+bx,0m=ay,n))+by,(m) 7n=-a0 .满足线性 Tx(nxmx() 1=-00 n-k n-k)=∑x(m) m=-00 .y(n-k)=T[x(n-k] 满足时不变性
1.13(3) 满足时不变性 满足线性 而 设 ( ) [ ( )] ( ) ( ) [ ( )] ( ) ( ) [ax ( ) x ( )] ( ) ( ) ( ) ( ) ( ) [x ( )] ( ) ( ) [x ( )] ( ), , 1 2 1 2 1 2 2 2 2 1 1 1 y n k T x n k y n k x m T x n k x m k x u T n b n ax m bx m ay n by n y n T n x m y n T n x m n k m n k u m k u m k u n m n m n m n m − = − − = − = − = + = + = + = = = = − =− − =− − = = + =− =− =− =−