
3.1 己知模拟系统函数H,(S)=+4s+3 3 试用脉冲响应不变法将以上模拟系统函数转换不数字系统函数H(), 采样周期T=0.5 3 3 3 H(s)=g2+4s+3 2+2 5+1s+3 3 3 H() A 2 2 1-esi 1-el 1-e3T2 3 3 2 2 e5-e 1-e-05T1-ei51-(e05+e15)+e22
3.1 0.5 1.5 1 2 2 0.5 1.5 1 0.5 1 1.5 1 1 1 3 1 1 1 2 2 1 ( ) ( ) 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 ( ) 3 2 3 1 2 3 4 3 3 ( ) 0.5 ( ), 4 3 3 ( ) − − − − − − − − − − − − − • − − • − = − − + + − = − − − = − − − = − = + − + + = + + = = + + = e e z e z e e z e z e z e z e z e z A H z s s s s H s T H z s s H s T T N i S T i a a i 采样周期 试用脉冲响应不变法将以上模拟系统函数转换不数字系统函数 已知模拟系统函数
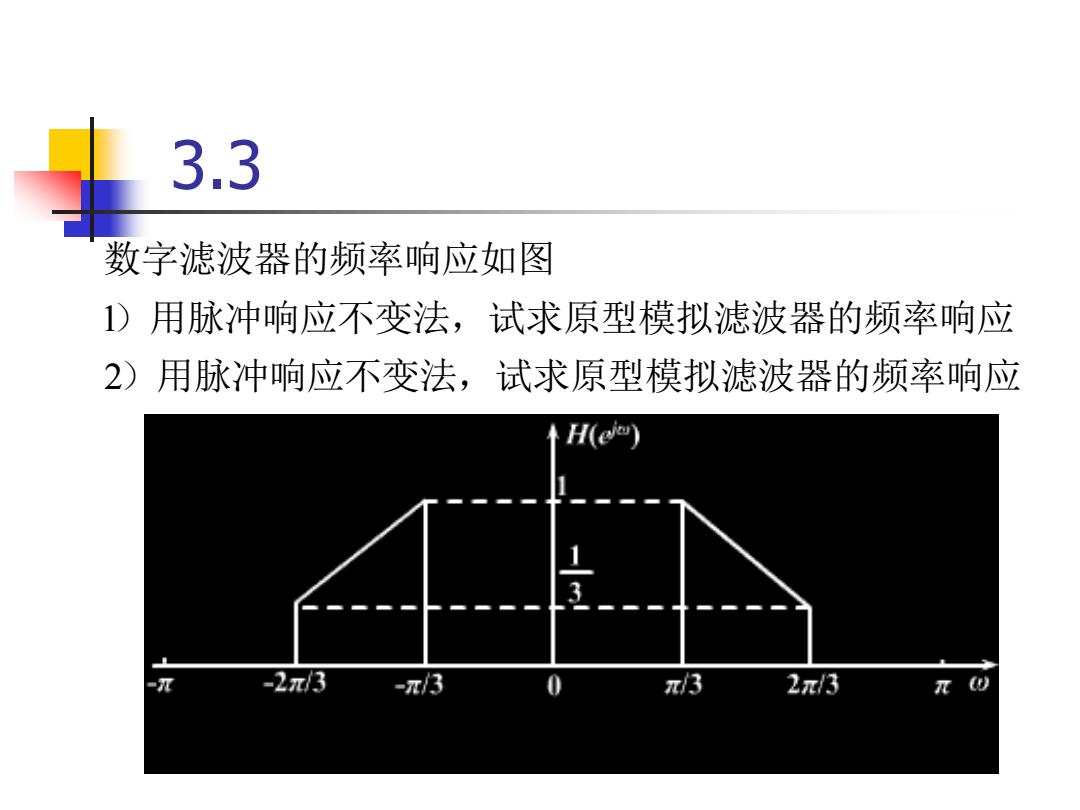
3.3 数字滤波器的频率响应如图 1)用脉冲响应不变法,试求原型模拟滤波器的频率响应 2)用脉冲响应不变法,试求原型模拟滤波器的频率响应 H(e▣ -2π/3 -π/3 π/3 2π/3
3.3 )用脉冲响应不变法,试求原型模拟滤波器的频率响应 )用脉冲响应不变法,试求原型模拟滤波器的频率响应 数字滤波器的频率响应如图 2 1

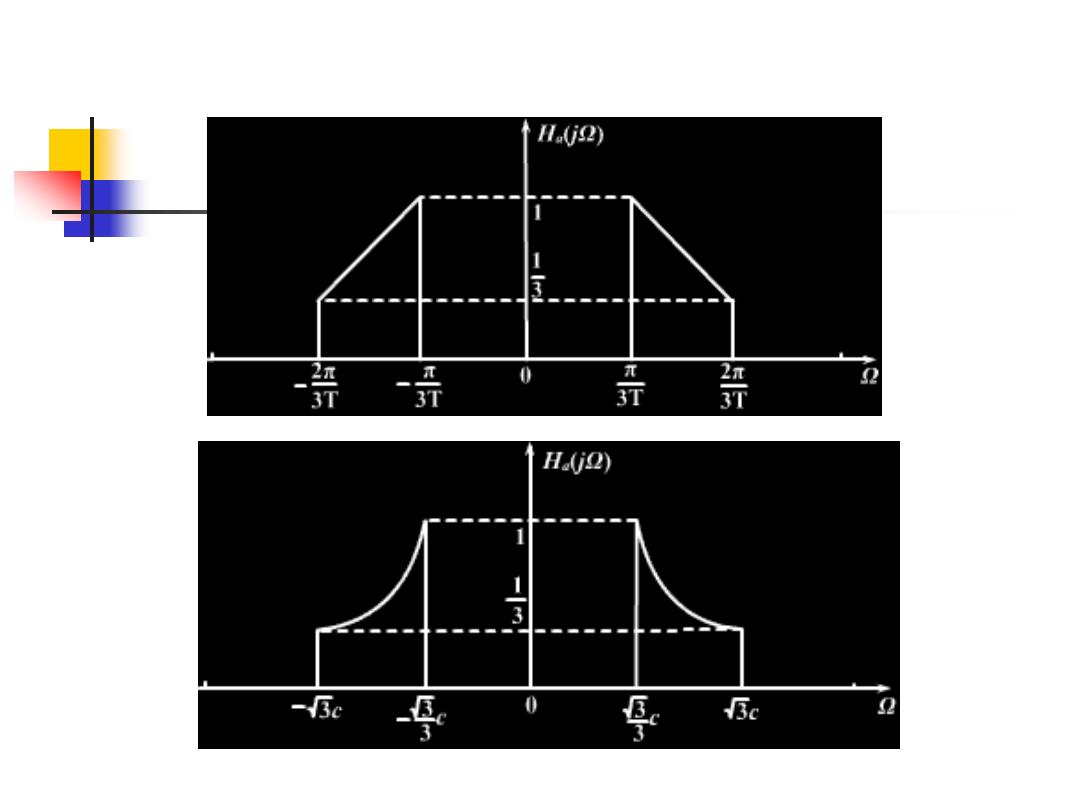
)脉冲响应不变法 因为o大于折叠频率时H(e)为零,故用此法无失真。 枚e)=,U学, 由图可得: 2 5 2π π 0+ ≤0≤- π 3 3 3 2. H(eo)={-二o+ 5元0 2π π 33 3 0,[-π,]之间的其他o 又由0=号则有 5 2T+ 2π π ≤2≤ π 3 3T 3T Ha(j)-H(e0)o=oT 20T+ 2 ≤2≤ 2π π ’3T 3T 0, 人 之间的其他Ω
− − + + − − = − − + + − − = = , 之间的其他 = = 又由 ,则有 , 之间的其他 由图 可得: 故 因为 大于折叠频率时 为零,故用此法无失真。 )脉冲响应不变法 = 0 [ , ] 3 2 3 , 3 5 T 2 3 3 2 , 3 5 T 2 ( ) ( ) 0 [ , ] 3 2 3 , 3 2 5 3 3 2 , 3 2 5 ( ) ( ), 1 ( ) ( ) 1 T T T T T H j H e T H e T H j T H e H e j a j a j j

(2)双线性变换法 根据双线性变换公式可得:故 HUj2)=H.jcg2〉 →2=cg(号) →o=arctg 4 25 arctg -V3css-3 π C 4 尊snR 0 其它2
(2) 双线性变换法 根据双线性变换公式可得: 故 ( ) c arctg c tg H j H j c tg a a = = = ) 2 ( ) 2 ( ) ( + − + − − = 其它 , 0 , 3 3 3 3 4 5 3 3 , 3 3 4 5 ( ) c c c arctg c c c arctg H j a
H02) -异 红 0 T 2 3T H(j2) 3 c-0 2