
目录M 11.3A/D转换器. .524 11.3.1A/D转换的基本原理.524 11.3.2取样-保持电路.527 11.3.3并联比较型A/D转换器. 529 11.3.4反馈比较型A/D转换器.532 11.3.5双积分型A/D转换器.535 11.3.6V-F变换型A/D转换器.539 11.3.7A/D转换器的转换精度与转换速度. .545 水章小结.547 习题 .548 附录 .555 附录一(电气图用图形符号一二进制逻辑单元》(GB4728.12一85)简介.555 附录二基本逻辑单元图形符号对照表 .566 部分习题答案 ,568 参考文献 .584 名词索引 .586

第一章 数制和码制 内容提要 本章首先介绍有关数制和码制的一些基本概念和术语,然后给出数字电路中常用的 数制和编码。此外,还将具体讲迷不同数制之间的转换方法和二进制数算数远算的原理 和方法。 1.1概述 我们知道,数字电路需要处理的是各种数字信号,那么这种数字信号有什么 特点呢? 心留心观察一下自然界中形形色色的物理量时不难发现,就其变化规律的特 点而言,它们不外乎两大类。其中一类物理量的变化在时间上和数量上都是离 散的,也就是说,它们的变化在时间上是不连续的,总是发生在一系列离散的瞬 间。而且,它们数值的大小和每次的增减变化都是某一个最小数量单位的整数 倍,而小于这个最小数量单位的数值没有任何物理意义。我们把这一类物理量 称为数字量,把表示数字量的信号称为数字信号,并把工作在数字信号下的电子 电路称为数字电路。例如,我们统计通过某一个桥梁的汽车数量,得到的就是 个数字量,最小数量单位的“1”代表“一辆”汽车,小于1的数值已经没有任何物 理意义。 另外一类物理量的变化在时间上或在数值上则是连续的。我们把这一类物 理量称为模拟量,把表示模拟量的信号称为模拟信号,并把工作在模拟信号下的 电子电路称为模拟电路。例如,热电偶工作时输出的电压或电流信号就是一科 模拟信号,因为被测的温度不可能发生突跳,所以测得的电压或电流无论在时间

2第一章数制和码制 上还是在数量上都是连续的。而且,这个信号在连续变化过程中的任何一个取 值都有具体的物理意义,即表示一个相应的温度。 随着计算机科学与技术突飞猛进地发展,用数字电路进行信号处理的优势 也更加突出。为了充分发挥和利用数字电路在信号处理上的强大功能,我们可 以先将模拟信号按比例转换成数字信号,然后送到数字电路(可以是专用的数 字信号处理电路,也可以是通用的计算机)进行处理,最后再将处理结果根据需 要转换为相应的模拟信号输出。自20世纪70年代开始,这种用数字电路处理 模拟信号的所谓“数字化”浪潮已经席卷了电子技术几乎所有的应用领域。 数字信号通常都是用数码形式给出的。不同的数码可以用来表示数量的不 同大小。用数码表示数量大小时,仅用一位数码往往不够用,因此经常需要用进 位计数制的方法组成多位数码使用。我们把多位数码中每一位的构成方法以及 从低位到高位的进位规则称为数制。在数字电路中经常使用的计数进制除了我 们最熟悉的十进制以外,更多的是使用二进制和十六进制。有时也用到八进制。 当两个数码分别表示两个数量大小时,它们可以进行数量间的加、减、乘、除 等运算。这种运算称为算数运算。由于目前数字电路中的算数运算最终都是以 二进制运算进行的,所以在这一章里我们还将比较详细地讨论在数字电路中是 采取什么方式完成二进制算数运算的。 不同的数码不仅可以用来表示数量的不同大小,而且可以用来表示不同的 事物或事物的不同状态。在用于表示不同事物的情况下,这些数码已经不再具 有表示数量大小的含义了,它们只是不同事物的代号而已。这些数码称为代码。 例如在举行长跑比赛时,为便于识别运动员,通常要给每一位运动员编一个号 码。显然,这些号码仅仅表示不同的运动员而已,没有数量大小的含义。 为了便于记忆和查找,在编制代码时总要遵循一定的规则,这些规则就称为 码制。每个人都可以根据自己的需要选定编码规则,编制出一组代码。考虑到 信息交换的需要,还必须制定一些大家共同使用的通用代码。例如目前国际上 通用的美国信息交换标准代码(ASCI码,见本章1.5节)就属于这一种。 1.2几种常用的数制 一、十进制 十进制是日常生活和工作中最常使用的进位计数制。在十进制数中,每 位有0~9十个数码,所以计数的基数是10。超过9的数必须用多位数表示,其 中低位和相邻高位之间的关系是“逢十进一”,故称为十进制。例如

1.2几种常用的数制3 143.75=1×102+4×10+3×10°+7×10-1+5×10- 所以任意一个十进制数D均可展开为 D=∑k,×10 (1.2.1) 式中k:是第i位的系数,它可以是0~9这十个数码中的任何一个。若整数部分 的位数是n,小数部分的位数为m,则i包含从n-1到0的所有正整数和从-1 到-m的所有负整数。 若以N取代式(1.2.1)中的10,即可得到任意进制(N进制)数按十进制展 开式的普遍形式 D=∑kN (1.2.2) 式中i的取值与式(1.2.1)的规定相同。N称为计数的基数,k为第i位的系 数,W称为第i位的权。 二、二进制 目前在数字电路中应用最广泛的是二进制。在二进制数中,每一位仅有0 和1两个可能的数码,所以计数基数为2。低位和相邻高位间的进位关系是“逢 二进一”,故称为二进制。 根据式(1.2.2),任何一个二进制数均可展开为 D=>k21 (1.2.3) 并计算出它所表示的十进制数的大小。例如 (101.11)2=1×22+0×2+1×2°+1×2l+1×22 =(5.75)0 上式中分别使用下脚注2和10表示括号里的数是二进制数和十进制数。 有时也用B(Binary)和D(Decimal)代替2和l0这两个脚注。 三、八进制 在某些场合有时也使用八进制。八进制数的每一位有0~7八个不同的数 码,计数的基数为8。低位和相邻的高位之间的进位关系是“逢八进一”。任意 ,个八进制数可以按十进制数展开为 D=∑k81 (1.2.4) 并利用上式计算出与之等效的十进制数值。例如 (12.4)g=1×8+2×8°+4×8- =(10.5)0 有时也用0(0ctal)代替下脚注8,表示八进制数。 四、十六进制 十六进制数的每一位有十六个不同的数码,分别用0~9、A(10)、B(11)、 C(12)、D(13)、E(14)、F(15)表示。因此,任意一个十六进制数均可展开为
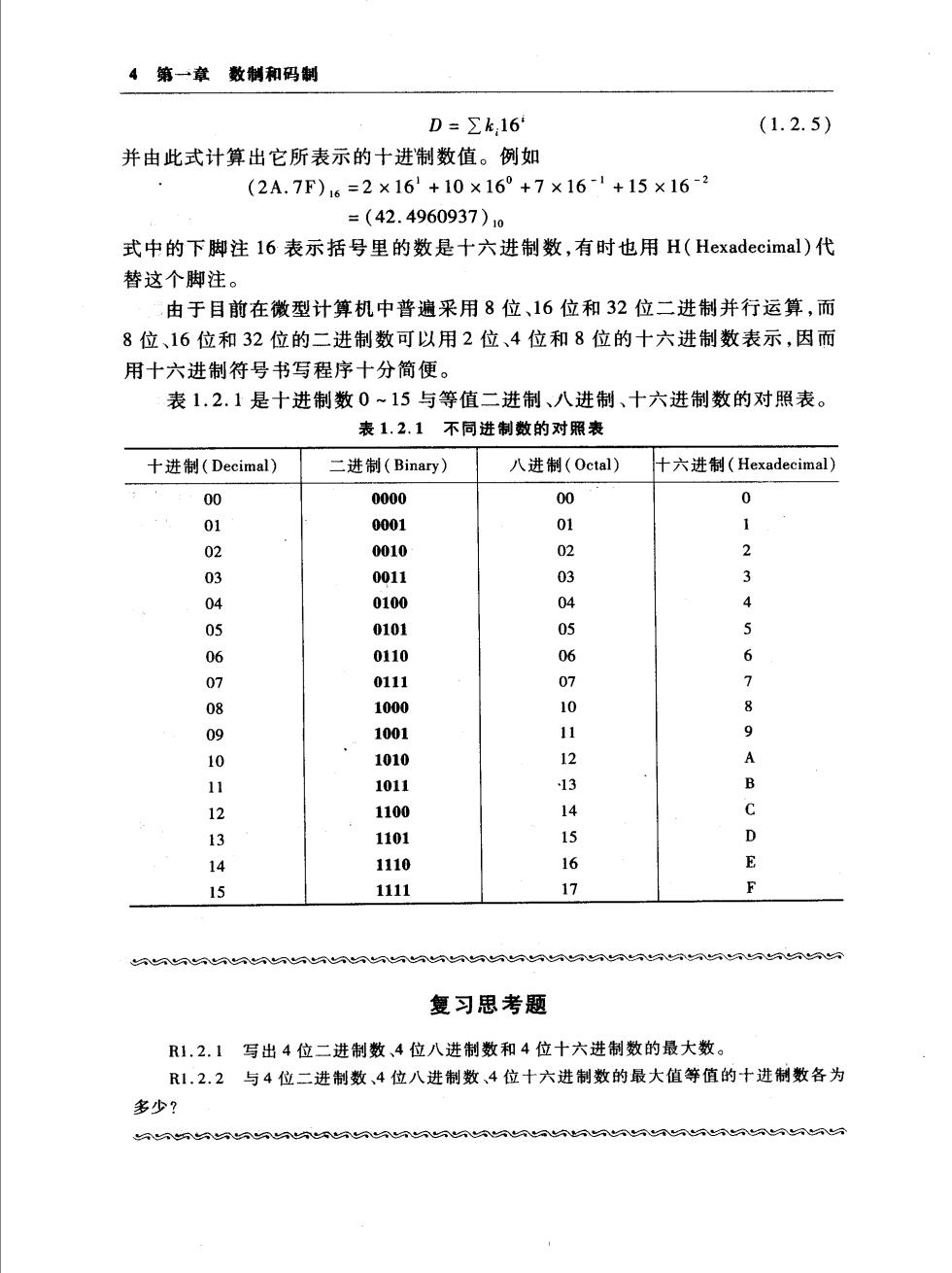
4第一章数制和码制 D=∑k,16 (1.2.5) 并由此式计算出它所表示的十进制数值。例如 (2A.7F)6=2×16+10×16°+7×16-+15×162 =(42.4960937)0 式中的下脚注16表示括号里的数是十六进制数,有时也用H(Hexadecimal)代 替这个脚注。 由于目前在微型计算机中普遍采用8位、16位和32位二进制并行运算,而 8位、16位和32位的二进制数可以用2位、4位和8位的十六进制数表示,因而 用十六进制符号书写程序十分简便。 表1.2.1是十进制数0~15与等值二进制、八进制、十六进制数的对照表。 表1.2.1不同进制数的对照表 十进制(Decimal) 二进制(Binary) 八进制(0ctal) 十六进制(Hexadecimal) 00 0000 00 0 01 0001 02 0010 02 0011 0100 04 05 0101 0110 6 0 0111 07 > 1000 1001 11 9 10 1010 12 1011 2 1100 13 1101 D 14 1110 E 1111 17 F 复习思考题 R1.2.1写出4位二进制数、4位八进制数和4位十六进制数的最大数。 R1,2.2与4位二进制数、4位八进制数、4位十六进制数的最大值等值的十进制数各为 多少?