式中v表示断面平均渗透速度,单位:mm/s K:渗透系数(mms),其物理意义是当水力坡降=l时的渗透速度。 达西定律说明:在层流状态的渗流中,渗流速度ⅴ与水力坡降的一次方成正比,并与土的性质有关。 斯托克斯简化的粘滞流体运动方程: △2 8n As 渗透流速ⅴ并不是土孔隙中水的实际平均流速。因为公式推导中采用的是土样的整个断面积,其中包括了土 粒骨架所占的部分面积在内。 土粒本身是不能透水的,故真实的过水面积Av应小于A,从而实际平均流速应大于V。一般称V为假想渗 流速度ⅴ与vs的关系可通过水流连续原理建立 vs=v/n 为了研究方便,渗流计算中均采用假想的平均流速。 以下两种情况不适用达西定律: (1)粗粒土,水力梯度较大时水流动为紊流: (2)对于密实的粘土,由于吸着水具有较大的粘滞阻力,因此只有当水力坡降达到某一数值,克服了吸着 水的粘滞阻力以后,才能发生渗透。我们将这一开始渗透时的水力坡降称为粘性土的起始水力坡降0 达西定律可修改为 v=k(6-i0) 4.3渗透系数的测定 一、实验室测定法: 1.常水头试验法,适合透水性大的砂性土 V k= n AA 2,变水头试验法,适合透水性小的无粘性土 2.3ad k= -log 402-) 水头管 ,= dh △ht t=t △h, 开关 (a)常水头试验 (b)变水头试险 二、现场抽水试验:
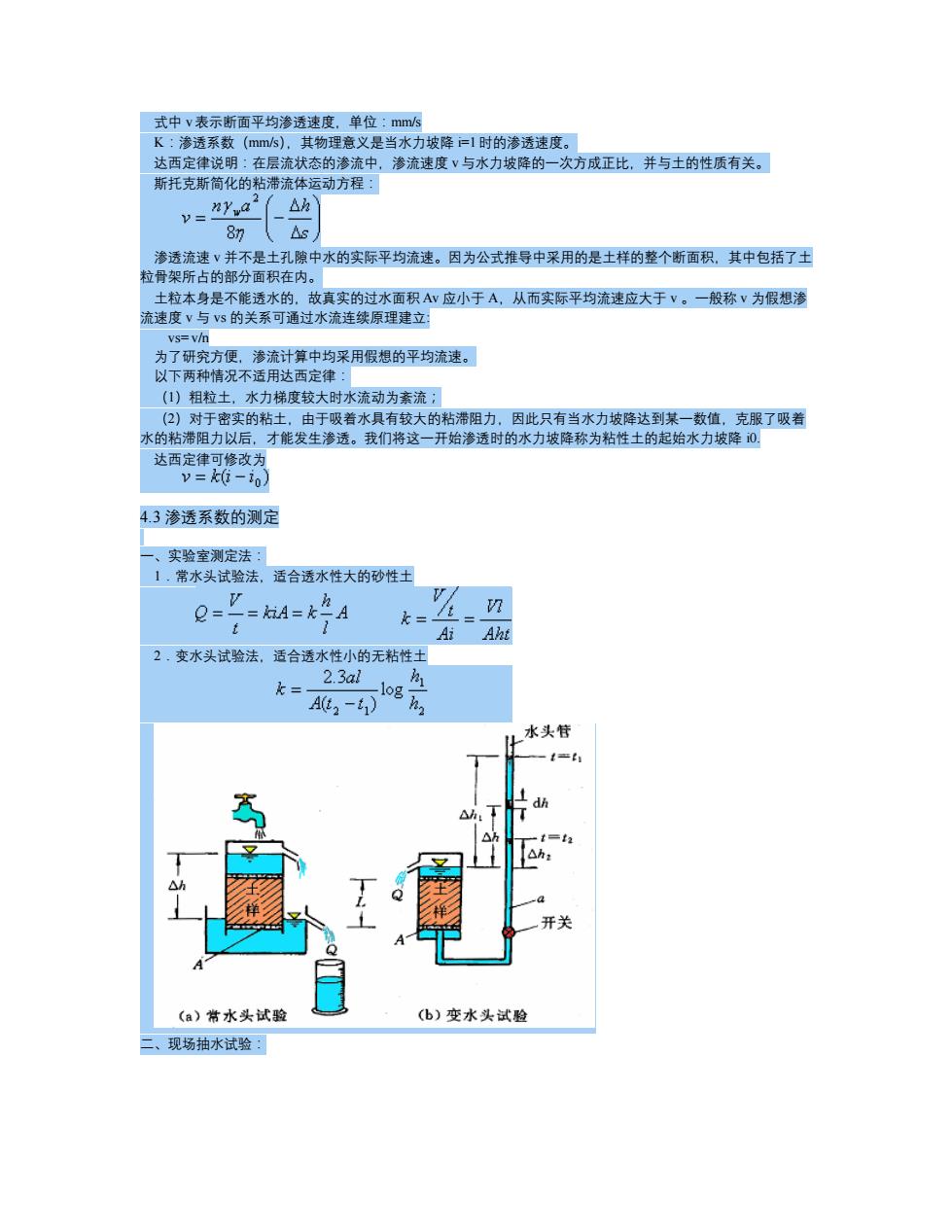
式中 v表示断面平均渗透速度,单位:mm/s K:渗透系数(mm/s),其物理意义是当水力坡降 i=1 时的渗透速度。 达西定律说明:在层流状态的渗流中,渗流速度 v与水力坡降的一次方成正比,并与土的性质有关。 斯托克斯简化的粘滞流体运动方程: 渗透流速 v 并不是土孔隙中水的实际平均流速。因为公式推导中采用的是土样的整个断面积,其中包括了土 粒骨架所占的部分面积在内。 土粒本身是不能透水的,故真实的过水面积 Av 应小于 A,从而实际平均流速应大于 v 。一般称 v 为假想渗 流速度 v 与 vs 的关系可通过水流连续原理建立: vs= v/n 为了研究方便,渗流计算中均采用假想的平均流速。 以下两种情况不适用达西定律: (1)粗粒土,水力梯度较大时水流动为紊流; (2)对于密实的粘土,由于吸着水具有较大的粘滞阻力,因此只有当水力坡降达到某一数值,克服了吸着 水的粘滞阻力以后,才能发生渗透。我们将这一开始渗透时的水力坡降称为粘性土的起始水力坡降 i0. 达西定律可修改为 4.3 渗透系数的测定 一、实验室测定法: 1.常水头试验法,适合透水性大的砂性土 2.变水头试验法,适合透水性小的无粘性土 二、现场抽水试验:

2.30 无压井抽水试验 k= π- log 承压井抽水试验 k= OIn(R/) 2πD(H-h) 三、经验公式: 哈臣(A.Hazen)提出砂质土的渗透系数k k=11.5)d品 太沙基提出了考虑土体孔隙比e的经验公式 k=2die? 四、成层土的等效渗透系数 (一)水平向渗流 水平渗流的特点: (1)各层土中的水力坡降i=(Dh/L)与等效土层的平均水力坡降i相同。 (2)垂直x2面取单位宽度,通过等效土层H的总渗流量等于各层土渗流量之和,即 gx=91x+g2x十g3x+…=∑9x 将达西定律代入上式可得沿水平方向的等效渗透系数kx: kx= 二)竖直向渗流 竖直渗流的特点: ()根据水流连续原理,流经各土层的流速与流经等效土层的流速相同,即 M=以3=3=…=V (2)流经等效土层H的总水头损失h等于各层上的水头损失之和,即 △h=△%+△22+△%+…=Z△% (3)将达西定律代入上式可得沿竖 i-1 直方向的等效渗透系数kz: H 五、影响渗透系数的因素 1土的粒度成分和矿物成分的影响:土的颗粒大小,形状及级配,影响土中空隙大小及形状,因而影响渗透 性。 2土的结构的影响:天然土层通常不是各向同性的,在渗透性方面往往也是如此。 3土中气体的影响:当土孔隙中存在密闭气泡时,会阻塞水的渗流,从而降低了的渗透性。 4水的性质对渗透系数的影响:与粘滞度有关。 4.4渗透力和渗透变形 一、渗透力 水在土体中流动时,将会引起水头的损失,而这种损失是由于水在土体孔隙中流动时,力图拖曳土粒时而消 耗能量的结果。我们将渗透水流施于单位土体内土粒上的拖曳力称为渗透力。 j=%-- _=Yw
三、经验公式: 哈臣(A.Hazen)提出砂质土的渗透系数 k 太沙基提出了考虑土体孔隙比 e 的经验公式 四、成层土的等效渗透系数 (一)水平向渗流 水平渗流的特点: (1) 各层土中的水力坡降 i=(Dh/L)与等效土层的平均水力坡降 i相同。 (2) 垂直 x-z面取单位宽度,通过等效土层 H 的总渗流量等于各层土渗流量之和,即 将达西定律代入上式可得沿水平方向的等效渗透系数 kx: (二)竖直向渗流 竖直渗流的特点: (1)根据水流连续原理,流经各土层的流速与流经等效土层的流速相同,即 (2)流经等效土层 H 的总水头损失 h等于各层上的水头损失之和,即 (3)将达西定律代入上式可得沿竖 直方向的等效渗透系数 kz: 五、影响渗透系数的因素 1.土的粒度成分和矿物成分的影响:土的颗粒大小,形状及级配,影响土中空隙大小及形状,因而影响渗透 性。 2.土的结构的影响:天然土层通常不是各向同性的,在渗透性方面往往也是如此。 3.土中气体的影响:当土孔隙中存在密闭气泡时,会阻塞水的渗流,从而降低了的渗透性。 4.水的性质对渗透系数的影响:与粘滞度有关。 4.4 渗透力和渗透变形 一、渗透力 水在土体中流动时,将会引起水头的损失,而这种损失是由于水在土体孔隙中流动时,力图拖曳土粒时而消 耗能量的结果。我们将渗透水流施于单位土体内土粒上的拖曳力称为渗透力

二、流砂、管涌 在向上的渗透水流作用下,表层土局部范围内的土体或颗粒群同时发生悬浮、移动的现象称为流土或流砂。 在渗透水流作用下,土中的细颗粒在粗颗粒形成的孔隙中移动.以至流失;随者土的孔隙不断扩大,渗透流 速不断增加,较粗的颗粒也相继被水流逐渐带走,最终导致土体内形成贯通的渗流管道,造成土体塌陷,这种 现象称为管涌。 4.5二维渗流和流网 、 二维渗流运动微分方程 假设水为不可压缩的流体,其连续条件为 v,dz+vdx=(v,+ :dx)dz+(v:+ :di)dx 8x 8z dys0 0x& 上述稳定渗流场中的拉普拉斯方程,若设定势函数和流函数为共轭函数,则可得到 ao 8o 22 =0 82p,a20 3+ 2 =0 二、流网的绘制原则 (1)流线与等势线必须正交,且两者围成的网眼尽可能接近于正方形。 (2)流线为不透水边界。 (3)静水位下透水边界上总水头相等,是等势线。 (4地下水位线或浸润线是流线。 三、流网的绘制方法 (1)首先根据渗流场的边界条件,确定边界流线和边界等势线。 (2)根据绘制流网的另外两个要求,初步绘制流网。然后再自中央向两边画等势线,每根等势线要与流线正 交,并弯曲成曲线正方形。 (3)一般初绘的流网总不能完全符合要求,必须反复修改,直至大部分网格满足曲线正方形为止。 四、流网的应用 1.求测管水头 4h-4的 8 (1-05 11 2.求水力梯度 △H i= 3.确定渗流量 g=k严Ah 4.判断渗透破坏的可能性 五、流网的特性
二、流砂、管涌 在向上的渗透水流作用下,表层土局部范围内的土体或颗粒群同时发生悬浮、移动的现象称为流土或流砂。 在渗透水流作用下,土中的细颗粒在粗颗粒形成的孔隙中移动.以至流失;随着土的孔隙不断扩大,渗透流 速不断增加.较粗的颗粒也相继被水流逐渐带走,最终导致土体内形成贯通的渗流管道,造成土体塌陷,这种 现象称为管涌。 4.5 二维渗流和流网 一、二维渗流运动微分方程 假设水为不可压缩的流体,其连续条件为 上述稳定渗流场中的拉普拉斯方程,若设定势函数和流函数为共轭函数,则可得到 二、 流网的绘制原则 (1) 流线与等势线必须正交,且两者围成的网眼尽可能接近于正方形。 (2) 流线为不透水边界。 (3) 静水位下透水边界上总水头相等,是等势线。 (4) 地下水位线或浸润线是流线。 三、 流网的绘制方法 (1)首先根据渗流场的边界条件,确定边界流线和边界等势线。 (2)根据绘制流网的另外两个要求,初步绘制流网。然后再自中央向两边画等势线,每根等势线要与流线正 交,并弯曲成曲线正方形。 (3)一般初绘的流网总不能完全符合要求,必须反复修改,直至大部分网格满足曲线正方形为止。 四、 流网的应用 1. 求测管水头 2. 求水力梯度 3.确定渗流量 4. 判断渗透破坏的可能性 五、 流网的特性

显然,边界条件相同时,土体中流网的形状和土的渗透系数大小无关;在无浸润面的渗流中,流网的形状 也与上下游水头差的大小无关。 第5章地基中的应力计算 5.1概述 地基受荷以后将产生应力和变形,给建筑物带来两个工程问题,即土体稳定问题和变形问题。如果地基内部 所产生的应力在土的强度所允许的范围内,那么土体是稳定的,反之,土体就要发生破坏,并能引起整个地基 产生滑动而失去稳定,从而导致建筑物倾倒。地基中的应力,按照其因可以分为自重应力和附加应力两种: 自重应力:由土体本身有效重量产生的应力称为自重应力。一般而言,土体在自重作用下,在漫长的地质历史 上已压缩稳定,不再引起土的变形(新沉积土或近期人工充填土除外)。 附加应力:由于外荷(静的或动的)在地基内部引起的应力称为附加应力,它是使地基失去稳定和产生变形 的主要原因。 5.2土中的自重应力 在计算地基中的自重应力时,一般将地基作为半无限弹性体来考虑。由半无限弹性体的边界条件可知,其内 部任一与地面平行的平面或垂直的平面上,仅作用着竖向应力和水平向应力,而剪应力。 地基中某单元体离地面的距离乙,土的容重为,则单元体上竖直向自重应力等于单位面积上的土柱有效重 量,即 Oa=y2 可见,土的竖向自重应力随着深度直线增大。 地基中除有作用于水平面上的竖向自重应力外,在竖直面上还作用有水平向的侧向自重应力。由于地基中的 自重应力状态属于侧限应力状态,故r=g=0,且sx=3gy,根据广义虎克定理,侧向自重应力sx和sgy应与 sz成正比,而剪应力均为零,即 scx=scy=KOscz yz=tzx=0 式中K)一比例系数,称为土的侧压力系数或静止土压力系数。它是侧限条件下土中水平向有效应力与竖直向 有效应力之比。 若天然地面下深度z范围内各层土的厚度自上而下分别为hl、h2、.hn,成层土自重应力为高度:土柱中 各层土重的总和,可得到的计算公式: 天然地面 (a) (6) sc一天然地面下任意深度z处的竖向有效自重应力kPa); n一深度z范围内的土层总数
显然,边界条件相同时,土体中流网的形状和土的渗透系数大小无关;在无浸润面的渗流中,流网的形状 也与上下游水头差的大小无关。 第 5 章 地基中的应力计算 5.1 概述 地基受荷以后将产生应力和变形,给建筑物带来两个工程问题,即土体稳定问题和变形问题。如果地基内部 所产生的应力在土的强度所允许的范围内,那么土体是稳定的,反之,土体就要发生破坏,并能引起整个地基 产生滑动而失去稳定,从而导致建筑物倾倒。地基中的应力,按照其因可以分为自重应力和附加应力两种: 自重应力:由土体本身有效重量产生的应力称为自重应力。一般而言,土体在自重作用下,在漫长的地质历史 上已压缩稳定,不再引起土的变形(新沉积土或近期人工充填土除外)。 附加应力:由于外荷(静的或动的)在地基内部引起的应力称为附加应力,它是使地基失去稳定和产生变形 的主要原因。 5.2 土中的自重应力 在计算地基中的自重应力时,一般将地基作为半无限弹性体来考虑。由半无限弹性体的边界条件可知,其内 部任一与地面平行的平面或垂直的平面上,仅作用着竖向应力和水平向应力,而剪应力 。 地基中某单元体离地面的距离 z,土的容重为 ,则单元体上竖直向自重应力等于单位面积上的土柱有效重 量,即 可见,土的竖向自重应力随着深度直线增大。 地基中除有作用于水平面上的竖向自重应力外,在竖直面上还作用有水平向的侧向自重应力。由于地基中的 自重应力状态属于侧限应力状态,故 ex=ey=0,且 scx=scy,根据广义虎克定理,侧向自重应力 scx 和 scy应与 scz 成正比,而剪应力均为零,即 scx= scy= K0scz txy=tyz=tzx=0 式中 K0 ―比例系数,称为土的侧压力系数或静止土压力系数。它是侧限条件下土中水平向有效应力与竖直向 有效应力之比。 若天然地面下深度 z范围内各层土的厚度自上而下分别为 h1、h2、… hn,成层土自重应力为高度 z 土柱中 各层土重的总和,可得到的计算公式: sc— 天然地面下任意深度 z处的竖向有效自重应力(kPa); n — 深度 z范围内的土层总数

hi一第i层土的厚度(m); g一第1层土的天然重度 5.3基底压力和基底附加压力 基底压力的分布规律主要是取决于上部结构、基础的刚度和地基的变形条件,是三者共同作用的结果。 基础刚度的影响 柔性基础能随着地基土表面而变形.作用在基础底面上的压力分布与作用在基础上的荷载分布完全一样。因 此,若上部荷载均匀分布,基底接触压力也为均匀分布。 绝对刚性基础的基础底面保持平面,即基础各点的沉降大小一样,基础底面上的压力分布不同于上部荷载的 分布情况。 一、基底压力的简化计算 1.中心荷载下的基底压力 中心荷载下的基础,其所受荷裁的合力通过基底形心。基底压力假定为均匀分布,此时基底平均压力设计值 pkPa)按下式计算: F+G 卫= A 式中p一作用任基础上的竖向力设计值(kN),G一基础自重设计值及其上回填土重标准值的总重(kN): G=gGAd其中gG为基础及回填土之平均重度,一般取20kNm3,但在地下水位以下部分应扣去浮力,即取 10kN/m3;d为基础埋深,必须从设计地面或室内外平均设计地面算起(m):A一基底面积(m2),对矩形基础 A=b,I和b分别为矩形基底的长度和宽度(m)。 对于荷载沿长度方向均匀分布的条形基础,则沿长度方向截取一单位长度的截条进行基底平均压力设计值 p(kPa)的计算,此时上式中A改为b(m),而F及G则为基础截面内的相应值(kNm)。 2.偏心荷载下的基底压力 单向偏心荷载下的矩形基础如图所示。设计时通常取基底长边方向与偏心方向一致,此时两短边边缘最大压 力设计值pmax与最小压力设计值pmin(kPa)按材料力学短柱偏心受压公式计算: 卫mx F+G M Pmin 6 W 式中M一作用于矩形基底的力矩设计值(kN.m); W一基础底面的抵抗矩,W=b26(m)。 把偏心荷载(如图中虚线所示)的偏心矩=M/F+G)引入上式得: 0诚 F+G 6e (1± Dnin 凸 基底边缘的最大压力pmax为: 2(F+G) Pio= 36k 二、 基底附加压力 般情况下,建筑物建造前天然土层在自重作用下的变形早已结束。因此,只有基底附加压力才能引起地基 的附加应力和变形。 如果基础砌置在天然地面上,那末全部基底压力就是新增加于地基表面的基底附加压力。实际上,一般浅基 础总是埋置在天然地面下一定深度处,该处原有的自重应力由于开挖基坑而卸除。因此,建筑物建造后的基底 压力中应扣除基底标高处原有的土中自重应力后,才是基底平面处新增加于地基的基底附加压力,基底平均附 加压力设计值p0值按下式计算(如图): po=p-sc=p-god 式中p一基底平均压力设计值(kPa);sc一土中自重应力标准值,基底处sc=gOd(kPa);g0一基础底面标高以 上天然土层的加权平均重度,其中地下水位下土层的重度取有效重度;d一基础埋深,必须从天然地面算起
hi — 第 i层土的厚度(m); gi— 第 i层土的天然重度 5.3 基底压力和基底附加压力 基底压力的分布规律主要是取决于上部结构、基础的刚度和地基的变形条件,是三者共同作用的结果。 基础刚度的影响 柔性基础能随着地基土表面而变形,作用在基础底面上的压力分布与作用在基础上的荷载分布完全一样。因 此,若上部荷载均匀分布,基底接触压力也为均匀分布。 绝对刚性基础的基础底面保持平面,即基础各点的沉降大小一样,基础底面上的压力分布不同于上部荷载的 分布情况。 一、基底压力的简化计算 1. 中心荷载下的基底压力 中心荷载下的基础,其所受荷裁的合力通过基底形心。基底压力假定为均匀分布,此时基底平均压力设计值 p(kPa)按下式计算: 式中 p — 作用任基础上的竖向力设计值(kN); G — 基础自重设计值及其上回填土重标准值的总重(kN); G=gGAd,其中 gG 为基础及回填土之平均重度,一般取 20kN/m3,但在地下水位以下部分应扣去浮力,即取 10kN/m3;d 为基础埋深,必须从设计地面或室内外平均设计地面算起(m);A — 基底面积(m2),对矩形基础 A=lb,l和 b分别为矩形基底的长度和宽度(m)。 对于荷载沿长度方向均匀分布的条形基础,则沿长度方向截取一单位长度的截条进行基底平均压力设计值 p(kPa)的计算,此时上式中 A 改为 b(m),而 F 及 G 则为基础截面内的相应值(kN/m)。 2.偏心荷载下的基底压力 单向偏心荷载下的矩形基础如图所示。设计时通常取基底长边方向与偏心方向一致,此时两短边边缘最大压 力设计值 pmax 与最小压力设计值 pmin (kPa)按材料力学短柱偏心受压公式计算: 式中 M — 作用于矩形基底的力矩设计值(kN.m); W — 基础底面的抵抗矩,W=bl2/6(m)。 把偏心荷载(如图中虚线所示)的偏心矩 e=M/(F+G)引入上式得: 基底边缘的最大压力 pmax 为: 二、基底附加压力 一般情况下,建筑物建造前天然土层在自重作用下的变形早已结束。因此,只有基底附加压力才能引起地基 的附加应力和变形。 如果基础砌置在天然地面上,那末全部基底压力就是新增加于地基表面的基底附加压力。实际上,一般浅基 础总是埋置在天然地面下一定深度处,该处原有的自重应力由于开挖基坑而卸除。因此,建筑物建造后的基底 压力中应扣除基底标高处原有的土中自重应力后,才是基底平面处新增加于地基的基底附加压力,基底平均附 加压力设计值 p0 值按下式计算(如图): p0= p - sc = p- g0d 式中 p —基底平均压力设计值(kPa); sc—土中自重应力标准值,基底处 sc=g0d (kPa);g0—基础底面标高以 上天然土层的加权平均重度,其中地下水位下土层的重度取有效重度; d—基础埋深,必须从天然地面算起