
当发送信号为S(t)时,y(t)的条 件概率密度函数为 f(y)= 2z0入exp([0-s(rdm 又称为似然函数 根据y(t)的统计特性,并遵循一定的 准则,即可作出正确的判决,判决空间中可 能出现的状态r1,2:,「m与y1 Y2,ym一一对应。 6
6 当发送信号为si (t)时,y(t)的条 件概率密度函数为 又称为似然函数 根据y(t)的统计特性,并遵循一定的 准则,即可作出正确的判决,判决空间中可 能出现的状态r1,r2,.,rm与y1, y2,.,ym一一对应。 [ ( ) ( )] } 1 exp{ ( 2 ) 1 ( ) 0 2 0 = − − T k i n s i y t s t dt n f y

10.2最佳接收的准则测 ■于 最小差错概率准则 在二进制数字调制中,发送信号只有两 个S1(t)和s2(t),假设s1(t)和s2(t)在观察时 刻的取值为a1和a2,则当发送信号为s1(t) 或S2(t)时,yt)的条件概率密度函数为: f(y)= (W2 .yexp-2rU0)-ard n f(y)= (xpn()-a.Fdi
7 10.2 最佳接收的准则 ◼ 最小差错概率准则 在二进制数字调制中,发送信号只有两 个s1 (t)和s2 (t), 假设s1 (t)和s2 (t)在观察时 刻的取值为a1和a2 ,则当发送信号为s1 (t) 或s2 (t)时, y(t)的条件概率密度函数为: [ ( ) ] } 1 exp{ ( 2 ) 1 ( ) 0 2 1 0 1 = − − T k n s y t a dt n f y [ ( ) ] } 1 exp{ ( 2 ) 1 ( ) 0 2 2 0 2 = − − T k n s y t a dt n f y
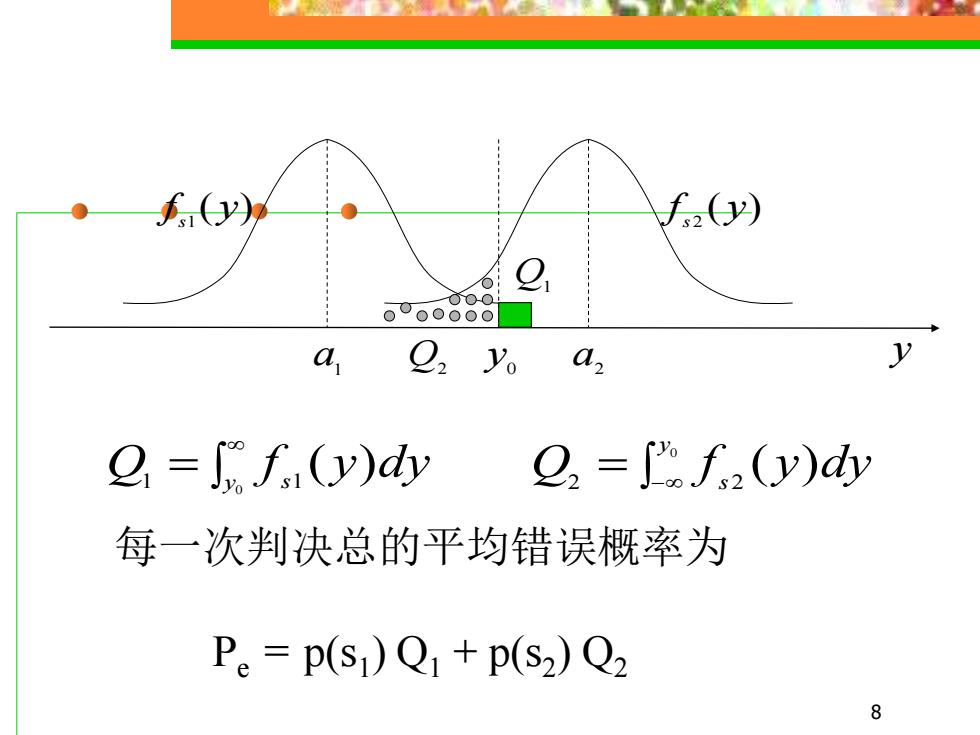
f() f(y) oo0000 C a, =f(y)dy 22=mf2(y)d 每一次判决总的平均错误概率为 Pe=p(S1)Q+p(S2)Q2 8
8 ( ) 1 f y s ( ) 2 f y s a1 0 a2 y y Q2 Q1 = 0 ( ) Q1 y f s1 y dy = − 0 ( ) 2 2 y Q f s y dy 每一次判决总的平均错误概率为 Pe = p(s1 ) Q1 + p(s2 ) Q2

一般p(S1),p(S2)认为是已知的,故Pe是yo 的函数 aP.。 e =-p(S)f(y)+p(s2)f2(y,)=0 8yo f.(Y.)_p(s2) 故 f2(vo) p(s) 为了达到最小错误概率,可按如下规则进行判决 f(y)、p(s2) 判为r1 f(y)p(s2) 判为r2 f,(y) p(S) f2(y) p(s) 似然比判决准测 9
9 一般 p(s1 ), p(s2 ) 认为是已知的,故Pe 是y0 的函数 ( 1 ) 1 ( 0 ) ( 2 ) 2 ( 0 ) 0 0 = − + = p s f y p s f y y P s s e ( ) ( ) ( ) ( ) 1 2 2 0 1 0 p s p s f y f y s s = ( ) ( ) ( ) ( ) 1 2 2 1 p s p s f y f y s s 故 为了达到最小错误概率,可按如下规则进行判决 判为r1 ( ) ( ) ( ) ( ) 1 2 2 1 p s p s f y f y s s 判为r2 似然比判决准则

若p(S1)=p(S2) 则 f(y)>f2(y) 判为S1 f(yf2(y) 判为s2 最大似然准则 ■ 根据最大似然准则,可以推出最佳接收机 结构 p(s)f (y)>p(s,)f.(y) 判为S1 p(s)f (y)<p(s2)f(y) 判为S2 p(s)exp:-SLy(t)-s,(O)T dt; 判为 P(s.)exp-Lv()-s.(OFdt3 S
10 若 p(s1 ) = p(s2 ) 则 ◼ 根据最大似然准则,可以推出最佳接收机 结构 ( ) ( ) 1 2 f y f y s s ( ) ( ) 1 2 f y f y s s 判为s1 判为s2 最大似然准则 ( ) ( ) ( ) ( ) 1 1 2 2 p s f y p s f y s s 判为S1 ( ) ( ) ( ) ( ) 1 1 2 2 p s f y p s f y s s 判为S2 ( )1 p s [ ( ) ( )] } 1 exp{ 0 2 1 0 − − T y t s t dt n [ ( ) ( )] } 1 exp{ 0 2 2 0 − − T y t s t dt n 判为S1 S2 ( )2 p s