秦 1.2 Jacobi选代 将矩阵A分裂为 A=D-L-U 其中D为A的对角线部分,-L和-U分别为A的严格下三角和严格上三角 部分。 在矩阵分裂A=M-N中取M=D,N=L+U,则可得Jacobi迭代算法: xk+1)=D-1(L+U)x+D-1b k=0,1,2, (6.3) 迭代矩阵为 G=D-1(L+U) http://math.ecnu.edu.cn/~jypan 11/86
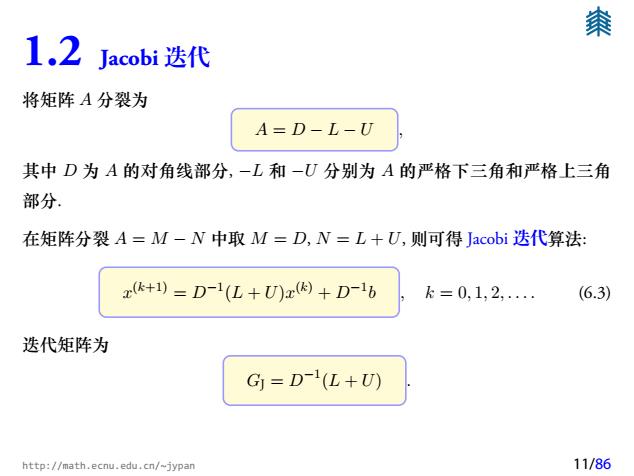
1.2 Jacobi 迭代 将矩阵 A 分裂为 A = D − L − U , 其中 D 为 A 的对角线部分, −L 和 −U 分别为 A 的严格下三角和严格上三角 部分. 在矩阵分裂 A = M − N 中取 M = D, N = L + U, 则可得 Jacobi 迭代算法: x (k+1) = D−1 (L + U)x (k) + D−1 b , k = 0, 1, 2, . . . . (6.3) 迭代矩阵为 GJ = D−1 (L + U) . http://math.ecnu.edu.cn/~jypan 11/86

写成分量形式即为 秦 x+= i=1,2,,n. ai j=1.j≠i 由于Jacobi迭代中x+)的更新顺序与i无关,即可以按顺序i=1,2,.,n 计算,也可以按顺序i=n,n-1,,2,1计算,或者乱序计算.因此Jacobi 迭代非常适合并行计算 http://math.ecnu.edu.cn/~jypan 12/86
写成分量形式即为 x (k+1) i = 1 aii bi − Xn j=1,j̸=i aijx (k) j , i = 1, 2, . . . , n. ✍ 由于Jacobi迭代中x (k+1) i 的更新顺序与 i 无关, 即可以按顺序i = 1, 2, . . . , n 计算, 也可以按顺序 i = n, n−1, . . . , 2, 1 计算, 或者乱序计算. 因此 Jacobi 迭代非常适合并行计算. http://math.ecnu.edu.cn/~jypan 12/86

秦 算法l.l求解线性方程组的Jacobi迭代方法 1:Choose an initial guess(0) 2:while not converge do 3: for i=1 to n do 4: 5: end for 6:end while 我们也可以将Jacobi迭代格式写为 r(k+1)=2(k)+D-1(b-Ac(k))=2(k)+D-irk k=0,1, 其中rk≌b一Ax(是k次迭代后的残量. http://math.ecnu.edu.cn/-jypan 13/86
算法 1.1 求解线性方程组的 Jacobi 迭代方法 1: Choose an initial guess x (0) 2: while not converge do 3: for i = 1 to n do 4: x (k+1) i = bi − Pn j=1,j̸=i aijx (k) j ! . aii 5: end for 6: end while 我们也可以将 Jacobi 迭代格式写为 x (k+1) = x (k) + D−1 (b − Ax(k) ) = x (k) + D−1 rk , k = 0, 1, . . . , 其中 rk ≜ b − Ax(k) 是 k 次迭代后的残量. http://math.ecnu.edu.cn/~jypan 13/86

秦 1.3 Gauss-Seidel送代 取M=D-L,N=U,即可得Gauss-Seidel(G-S)迭代算法: 2(k+1)=(D-L)-Uz(k)+(D-L)-16 (6.4) 迭代矩阵为 GGs=(D-L)-1U http://math.ecnu.edu.cn/~jypan 14/86
1.3 GaussSeidel 迭代 取 M = D − L, N = U, 即可得 GaussSeidel (GS) 迭代算法: x (k+1) = (D − L) −1Ux(k) + (D − L) −1 b (6.4) 迭代矩阵为 GGS = (D − L) −1U http://math.ecnu.edu.cn/~jypan 14/86

将G-S迭代改写为 秦 Dxk+1)=Lxk+)+Ux因+b, 即可得分量形式 2+ i=0,1,.,n. ai =i+1 http://math.ecnu.edu.cn/~jypan 15/86
将 GS 迭代改写为 Dx(k+1) = Lx(k+1) + Ux(k) + b, 即可得分量形式 x (k+1) i = 1 aii bi − X i−1 j=1 aijx (k+1) j − Xn j=i+1 aijx (k) j , i = 0, 1, . . . , n. http://math.ecnu.edu.cn/~jypan 15/86