
例4封装好的电路如图,已知下列实验数据研究激当us=IV,is=1A 时,响应 i=2A励和响当 us=-1V, is=2A 时,响应i=lA应关系求 us=-3V, is=5A 时,响应 i=?的实验方法i=kis +k,us解根据叠加定理us代入实验数据:[k+k,=2[ k, =1( k, =1[2k -k, =1无源线性i=us+is=-3+5=2A网络返上回页下页
• 例4 封装好的电路如图,已知下列实验数据: 当 uS =1V, i S =1A 时,响应 i = 2A 求 uS = −3V, i S = 5A 时, 响应 i =? 上 页 下 页 研究激 励和响 应关系 的实验 方法 当 uS = −1V, i S = 2A 时,响应 i =1A 解 根据叠加定理 S S i k i k u = 1 + 2 代入实验数据: 2 k1 + k2 = 2 1 k1 − k2 = 1 1 2 1 = = k k i = uS + i S = −3+ 5 = 2A 无源 线性 网络 uS i + - iS 返 回
例5R=2Q R=l R2=1Q u=51V,求电流i8A Ri21ARi3ARii-lA+21V十+3V-8V十十R2R2R2113ARLus5A2V2Aus,=34V解采用倒推法:设i=1A51u则即 i=i=×1=1.5Ai34uus返回上页下页
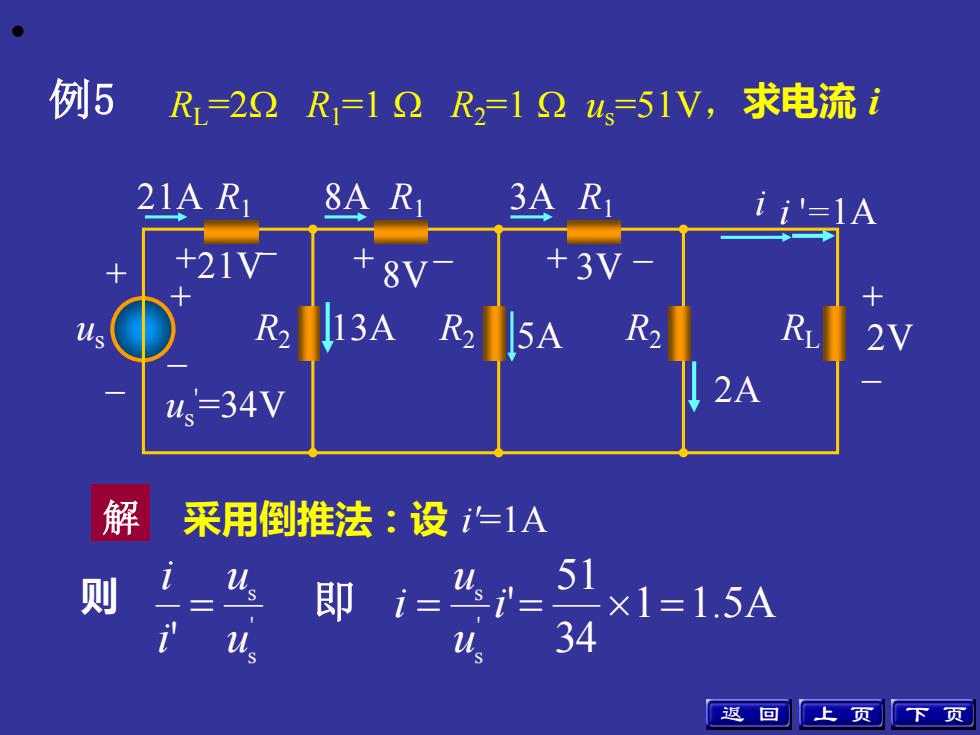
• R1 R1 R1 i R2 RL + – us R2 R2 例5 采用倒推法:设 i'=1A 则 R 求电流 i L=2 R1=1 R2=1 us=51V, + – 2V 2A + – + 3V – 8V + – 21V + – us '=34V 21A 8A 3A 13A 5A i '=1A 1 1.5A 34 51 ' ' ' s s ' s s = = i = = u u i u u i i 即 解 返 回 上 页 下 页
例6求图示电路的支路电压和电流5252i =110/[5 +(5+10) //10)解1113=10A110V102102ui =3i /5=6Ai =2i /5=4A替代u =10i, = 60V5252替代以后有:1213i =(110 -60)/5=10A102110Vi.=60/15=4A注意替代后各支路电压和电流完全不变返上回页下页
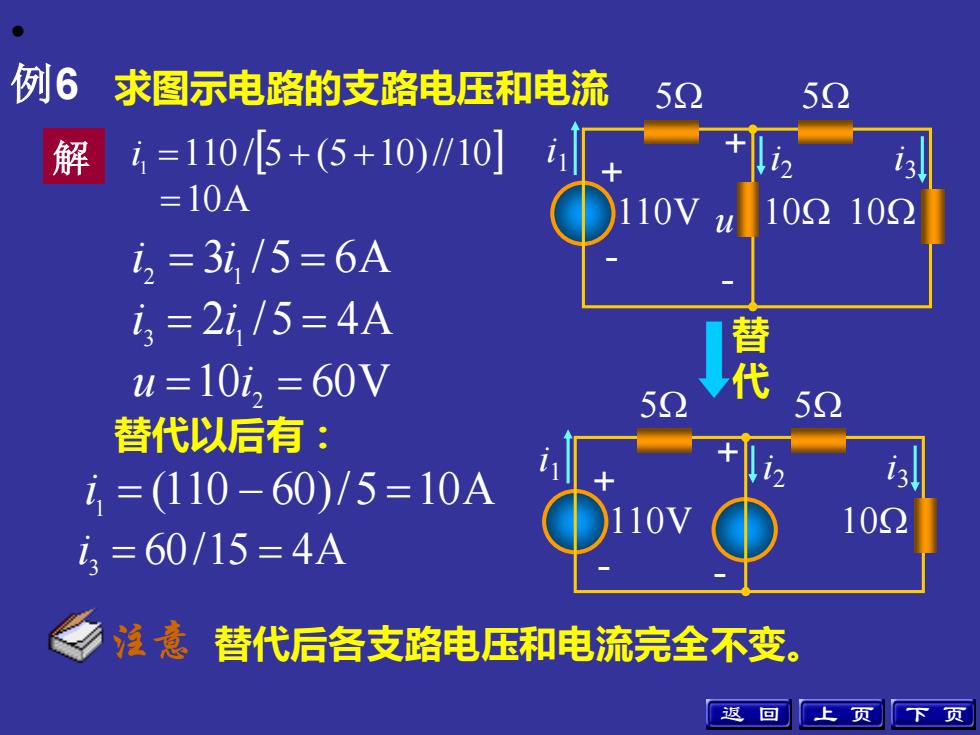
• 例6 求图示电路的支路电压和电流 解 10A 110 / 5 (5 10)//10 1 = i = + + i 2 = 3i 1 /5 = 6A i 3 = 2i 1 /5 = 4A u =10i 2 = 60V 替 代 替代以后有: i 1 = (110 − 60)/5 =10A i 3 = 60/15 = 4A 替代后各支路电压和电流完全不变。 上 页 下 页 + - i3 10 5 5 110V 10 i2 i1 + - u 注意 + - i3 10 5 5 110V i2 i1 + - 返 回
0.521-812试求Rx例7若使==L8解用替代:0.520.520.520.521Q2/128文0.520.520.520.52返上回页下页
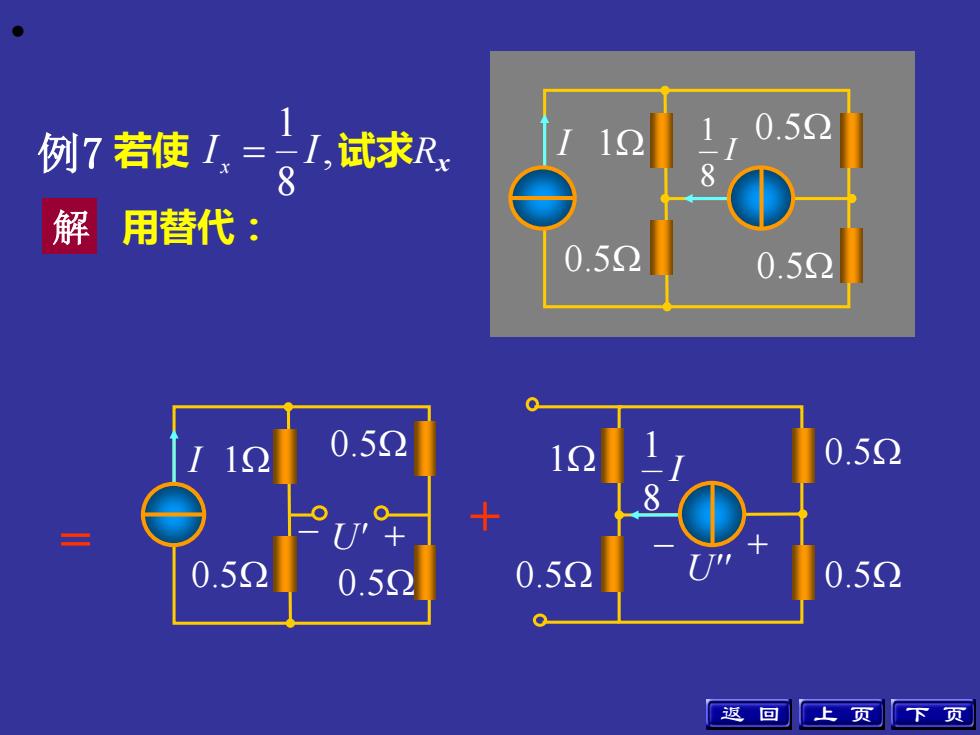
• 例7 若使 试求Rx , 8 1 I I x = 解 用替代: = + 上 页 下 页 – U' + 0.5 0.5 I 1 0.5 0.5 0.5 1 0.5 I 8 1 U'' – + 0.5 0.5 10V 3 1 Rx Ix – U + I 0.5 + - 0.5 0.5 I 1 0.5 I 8 1 返 回
0.520.52121018T0.520.520.520.521.51×0.5=0.112.52.51.5U"==I×1=-0.075IX82.5U-U+U"=-(0.1-0.075)/-0.0251R=U/0.1251-0.0251/0.125/-0.2Q返回上页下页
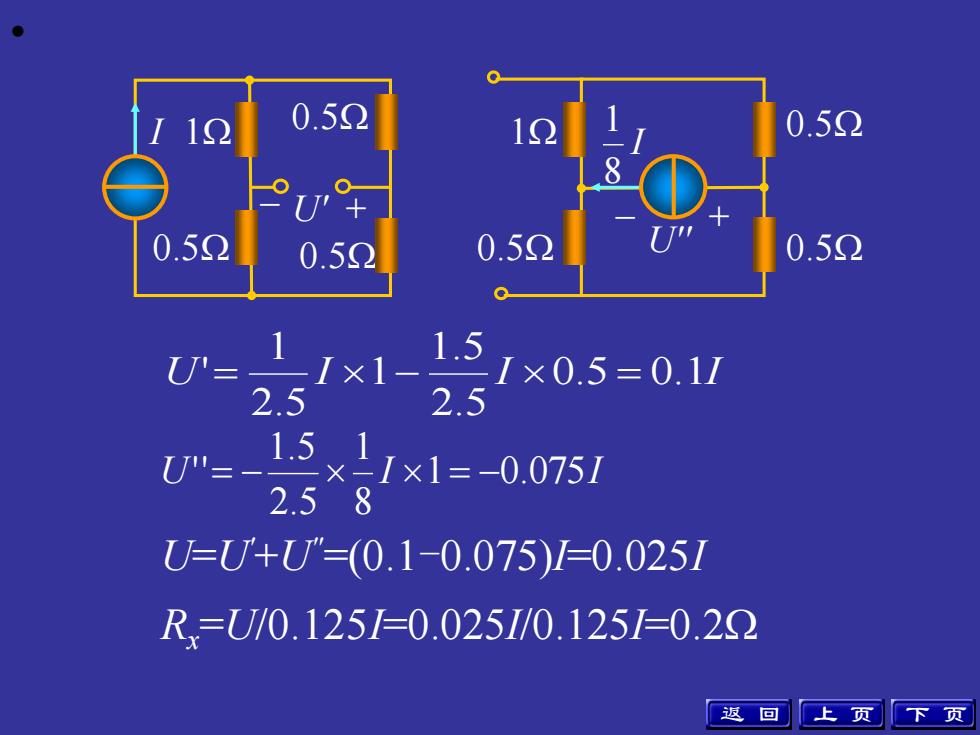
• U I I 0.5 0.1I 2.5 1.5 1 2.5 1 ' = − = U I 1 0.075I 8 1 2.5 1.5 '' = − = − 上 页 下 页 U=U'+U"=(0.1-0.075)I=0.025I Rx =U/0.125I=0.025I/0.125I=0.2 – U' + 0.5 0.5 I 1 0.5 0.5 0.5 1 0.5 I 8 1 U'' – + 返 回