
52一电路的初始值 独元始辑 (2)、换路定律(Switching Law) 若电容电流和电感电压山在t=t时为有限值,则换路前后瞬间电容 电压lC和电感电流i是连续的(不发生跃变),即有 uc(to+)=uc(to-) 西安电子科技大学电路与系统多媒体室制 iL(to+)=iL(to-) (3)、说明 (I)强调指出:除电容电压和电感电流外,其余各处电压电流不受 换路定律的约束,换路前后可能发生跃变。 (2)换路定律可以从能量的角度来理解: 由于wc()=0.5C2c(①)、wL()=0.5L2(t),如果e或发生跃变,则wc 或WL也发生跃变,由于功率p=dhw/dt,因此能量的跃变意味着功率为 0,这在实际电路中是不可能的。但在某些理想情况下,有可能。 (3)通常t=0。此时uc(0+)=4c(0),(0+)=ii(0-) 611页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 (2)、换路定律(Switching Law) 第 5-11 页 前一页 下一页 返回本章目录 5.2 电路的初始值 若电容电流iC和电感电压uL在t = t0时为有限值,则换路前后瞬间电容 电压uC和电感电流iL是连续的(不发生跃变),即有 uC(t0+ ) = uC(t0-) iL (t0+ ) = iL (t0-) (3)、说明 (1)强调指出:除电容电压和电感电流外,其余各处电压电流不受 换路定律的约束,换路前后可能发生跃变。 (2)换路定律可以从能量的角度来理解: 由于wC(t) = 0.5Cu2 C(t)、wL (t) = 0.5Li2 L (t),如果uC或iL发生跃变,则wC 或wL也发生跃变,由于功率p = dw/dt,因此能量的跃变意味着功率为 ∞,这在实际电路中是不可能的。但在某些理想情况下,有可能。 (3)通常t0= 0。此时uC(0+ ) = uC(0-), iL (0+ ) = iL (0-)

52一电路的初始值 独元初始缉 2、 独立初始值(初始状态)的求解 首先根据换路前电路的具体状况,求出u(0)和(0-)。 然后利用换路定律即可求得uc(0+)=u(0),i(0)=i(0)。 例:电路如图所示,已知<0时,开关S是闭合的,电路己处 西安电子科技大学电路 于稳定。在t=0时,开关S打开,求初始值uc(0)和(0)。 解:t<0时,电路在直流电源作用 42 下并已处于稳态,此时,电路各处 电压、电流均为直流。因此电容可 Us① 8V L 与系 视为开路,电感视为短路。得t= 2H 统多体 0-时的等效电路知图(b)。 由图(b)电路容易求得: 22 (a) 42 室制 i(0-)=8/(2+6)=1A 169 uc(0)=6i(0)=6V 8V i(0-) uc(O- 由换路定律得:uc(0+)=uc(0)=6V i(04)=(0)=1A (b)
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2、独立初始值(初始状态)的求解 第 5-12 页 前一页 下一页 返回本章目录 首先根据换路前电路的具体状况,求出uC(0-)和 iL (0-)。 然后利用换路定律即可求得uC(0+ ) = uC(0-), iL (0+ ) = iL (0-)。 例:电路如图所示,已知t<0时,开关S是闭合的,电路已处 于稳定。在t = 0时,开关S打开,求初始值uC(0+ ) 和iL (0+ ) 。 解:t < 0时,电路在直流电源作用 下并已处于稳态,此时,电路各处 电压、电流均为直流。因此电容可 视为开路,电感视为短路。得t = 0-时的等效电路如图(b)。 S 1F 2H US iL uC 2Ω 6Ω 4Ω 8V (a) S uC(0-) iL(0-) 2Ω 6Ω 4Ω 8V (b) 由图(b)电路容易求得: iL (0-) = 8/(2+6) = 1 A uC(0-) = 6 iL (0-) = 6 V 由换路定律得: uC(0+ ) = uC(0-) = 6 V iL (0+ ) = iL (0-) = 1 A 5.2 电路的初始值
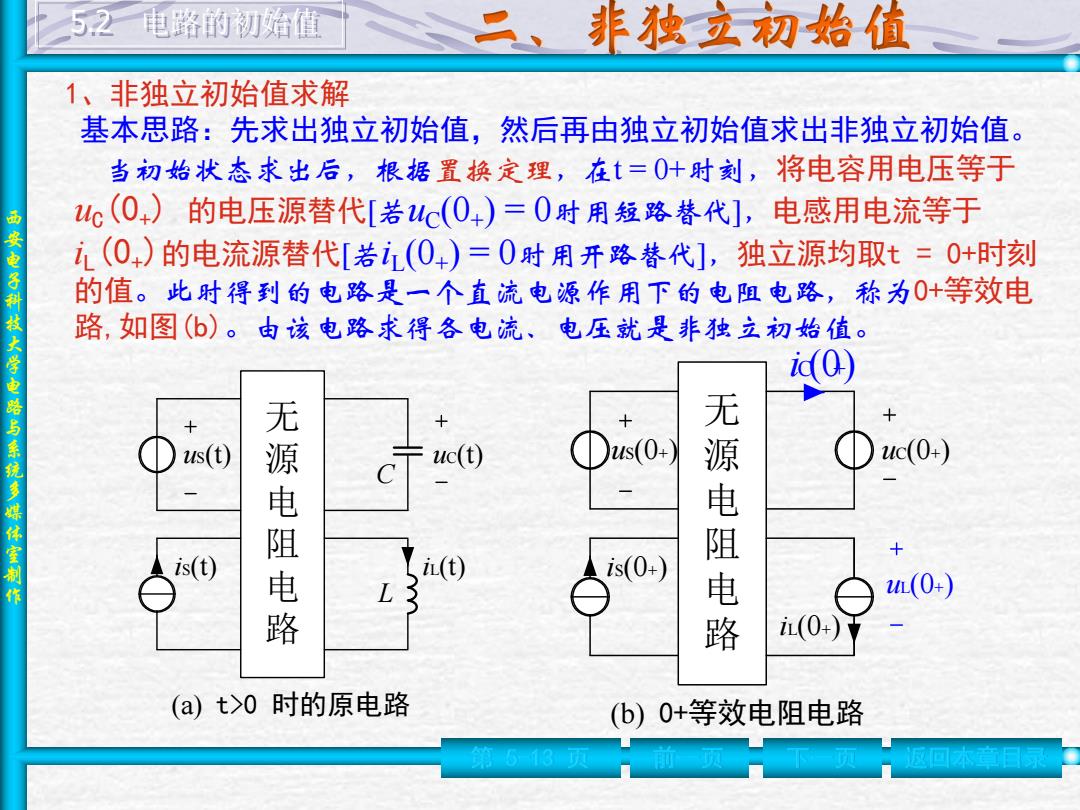
52一电路的初始值 二、非独立初始值 1、非独立初始值求解 基本思路:先求出独立初始值,然后再由独立初始值求出非独立初始值。 当初始状态求出后,根据置换定理,在=0十附刻,将电容用电压等于 c(0)的电压源替代[若uc(04)=0时用短路替代],电感用电流等于 西安电子科 (0+)的电流源替代[若(0+)=0时用开路替代],独立源均取t=0+时刻 的值。此时得到的电路是一个直流电源作用下的电阻电路,称为0+等效电 路,如图(b)。由该电路求得各电流、电压就是非独立初始值。 技大学电路与系统多媒体室制作 us(代 is(t) 无源电阻电路 uc(t) )us(0+ uc(0+) iL(t) is(0+) 无源电阻电路 (O) i(0+)六 (a)t>0时的原电路 (b)0+等效电阻电路 13项
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 1、非独立初始值求解 基本思路:先求出独立初始值,然后再由独立初始值求出非独立初始值。 第 5-13 页 前一页 下一页 返回本章目录 当初始状态求出后,根据置换定理,在t = 0+时刻,将电容用电压等于 uC(0+) 的电压源替代[若uC(0+ ) = 0时用短路替代],电感用电流等于 iL(0+)的电流源替代[若iL (0+ ) = 0时用开路替代],独立源均取t = 0+时刻 的值。此时得到的电路是一个直流电源作用下的电阻电路,称为0+等效电 路,如图(b)。由该电路求得各电流、电压就是非独立初始值。 无 源 电 阻 电 路 uS(t) iS(t) uC(t) iL(t) C L (a) t>0 时的原电路 无 源 电 阻 电 路 uS(0+) iS(0+) uC(0+) iL(0+) (b) 0+等效电阻电路 iC(0+) uL(0+) 5.2 电路的初始值