兰州交通大学：《电磁场与电磁波》课程教学资源（试卷习题）各章课后习题与解答

二章习题解答 21一个平行板真空二极管内的电荷体密度为p=-号6U,dx8,式中明极板位于 x=0,阳极板位于x=d,极间电压为U。。如果U。=40V、d=1cm、横截面S=10cm2, 求：(1)x=0和x=d区域内的总电荷量Q:(2)x=d/2和x=d区域内的总电荷量Q。 4 解(1) 0=Jpdr=[(-4 x)SdxS--4.72x10C =pdr=(Udvx)sdx=US=-097x10"c (2) 2.2一个体密度为p=2.32×10-7Cm3的质子束，通过1000V的电压加速后形成等速的 质子束，质子束内的电荷均匀分布，束直径为2mm,束外没有电荷分布，试求电流密度和电流。 解质子的质量m=1.7×102kg、电量g=1.6×10-19C。由 得 v=2mqU =1.37x10 m/s J=pv=0.318A/m2 1=Jπ(d/2)2=10-6A 2.3一个半径为α的球体内均匀分布总电荷量为Q的电荷，球体以匀角速度0绕一个直径 旋转，求球内的电流密度。 解以球心为坐标原点，转轴（一直径）为：轴。设球内任一点P的位置矢量为r,且与 z轴的夹角为日，则P点的线速度为 v-o×r=e,orsin0 球内的电荷体密度为 0 p=4元 J=m=品万mn0-器rsn0 2.4一个半径为a的导体球带总电荷量为Q,同样以匀角速度0绕一个直径旋转，求球表 面的面电流密度。 解以球心为坐标原点，转轴（一直径）为：轴。设球面上任一点P的位置矢量为r,且r 与z轴的夹角为日，则P点的线速度为 v=@xr=eoasine 球面的上电荷面密度为 0 =4πd 0 Qosine J,=m=e4raoasn8=e,4na

二章习题解答 2.1 一个平行板真空二极管内的电荷体密度为 4 3 2 3 0 0 4 9   U d x − − = − ，式中阴极板位于 x = 0 ，阳极板位于 x d = ，极间电压为 U0 。如果 0 U = 40V、d =1cm 、横截面 2 S =10cm ， 求：（1） x = 0 和 x d = 区域内的总电荷量 Q ；（2） x d = 2 和 x d = 区域内的总电荷量 Q 。 解 （1） 4 3 2 3 0 0 0 4 d ( ) d 9 d Q U d x S x     − − = = − =   11 0 0 4 4.72 10 C 3 U S d  − − = −  （2） 4 3 2 3 0 0 2 4 d ( ) d 9 d d Q U d x S x     − −   = = − =   11 0 0 3 4 1 (1 ) 0.97 10 C 3 2 U S d  − − − = −  2.2 一个体密度为 7 3  2.32 10 C m − =  的质子束，通过 1000V 的电压加速后形成等速的 质子束，质子束内的电荷均匀分布，束直径为 2 mm ，束外没有电荷分布，试求电流密度和电流。 解 质子的质量 27 m 1.7 10 kg − =  、电量 19 q 1.6 10 C − =  。由 1 2 2 mv qU = 得 6 v mqU = =  2 1.37 10 ms 故 J v = =  0.318 2 A m 2 6 I J d  ( 2) 10− = = A 2.3 一个半径为 a 的球体内均匀分布总电荷量为 Q 的电荷，球体以匀角速度  绕一个直径 旋转，求球内的电流密度。 解 以球心为坐标原点，转轴（一直径）为 z 轴。设球内任一点 P 的位置矢量为 r ，且 r 与 z 轴的夹角为  ，则 P 点的线速度为 rsin v r e =  =    球内的电荷体密度为 3 4 3 Q a   = 故 3 3 3 sin sin 4 3 4 Q Q r r a a          J v e e = = = 2.4 一个半径为 a 的导体球带总电荷量为 Q ，同样以匀角速度  绕一个直径旋转，求球表 面的面电流密度。 解 以球心为坐标原点，转轴（一直径）为 z 轴。设球面上任一点 P 的位置矢量为 r ，且 r 与 z 轴的夹角为  ，则 P 点的线速度为 asin v r e =  =    球面的上电荷面密度为 2 4 Q a   = 故 2 sin sin 4 4 S Q Q a a a          J v e e = = =

2.5两点电荷q=8C位于：轴上z=4处，2=-4C位于y轴上y=4处，求(4,0,0)处 的电场强度。 解电荷g在(4,0,0)处产生的电场为 子品 电荷42在(4,0,0)处产生的电场为 E=9- 1e,4-e,4 高-守而 故(4,0,0)处的电场为 E-E+B=ete-e.2 32√2π6。 2.6一个半圆环上均匀分布线电荷P,求垂直于圆平面的轴线上2=a处的电场强度 E(0,0,a),设半圆环的半径也为a,如题2.6图所示。 解半圆环上的电荷元P,dI'=P,ad'在轴线上z=a处的电场强度为 E-w- dE pe.-(e.cose,sind 82π5 a 在半圆环上对上式积分，得到轴线上z=a处的电场强度为 E(0,0,a)=dE- P le.-(e,cos'+e,sindee,2) 82π6an 8W2π8a 2.7三根长度均为L,均匀带电荷密度分别为P1、P2和p地 题2.6图 线电荷构成等边三角形。设Pm=2P2=2Ps,计算三角形中心处的 由场强度。 解建立题2.7图所示的坐标系。三角形中心到各边的距离为 d=an30=5L 6 3p1 E=6,4Ccs30-s150)=6,22 Eks+n0益e6+叠 E,=化，60s30-t,n30)i 3p%=e,5-,8 3p 故等边三角形中心处的电场强度为 题2.7图

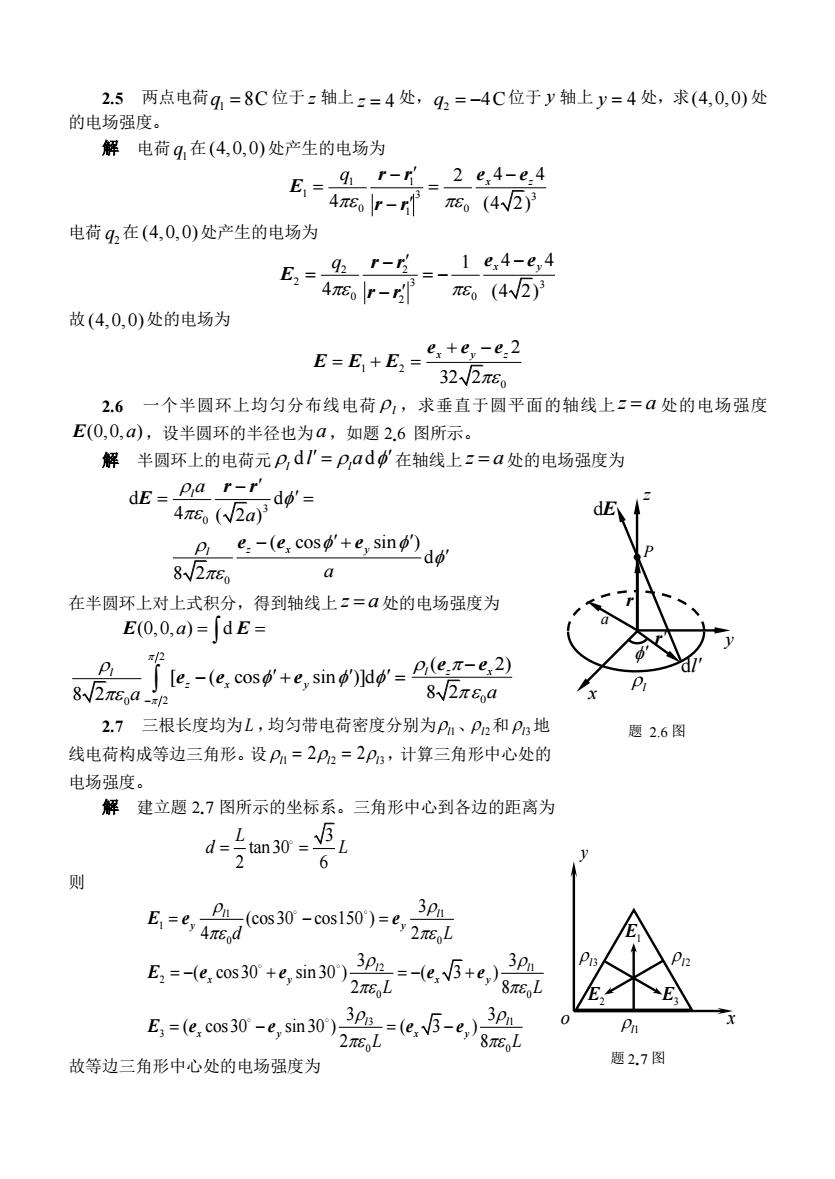
2.5 两点电荷 1 q = 8C 位于 z 轴上 z = 4 处， 2 q = −4C 位于 y 轴上 y = 4 处，求 (4,0,0) 处 的电场强度。 解 电荷 1 q 在 (4,0,0) 处产生的电场为 1 1 1 3 3 0 0 1 2 4 4 4 (4 2) q x z   −  − = = −  r r e e E r r 电荷 2 q 在 (4,0,0) 处产生的电场为 2 2 2 3 3 0 0 2 1 4 4 4 (4 2) q x y   −  − = = − −  r r e e E r r 故 (4,0,0) 处的电场为 1 2 0 2 32 2 x y z  + − = + = e e e E E E 2.6 一个半圆环上均匀分布线电荷  l ，求垂直于圆平面的轴线上 z a = 处的电场强度 E(0,0, ) a ，设半圆环的半径也为 a ，如题 2.6 图所示。 解 半圆环上的电荷元 d d l l    l a   = 在轴线上 z a = 处的电场强度为 3 0 d d 4 ( 2 ) l a a    −  = =  r r E 0 ( cos sin ) d 8 2 l z x y a      − +   e e e 在半圆环上对上式积分，得到轴线上 z a = 处的电场强度为 (0,0, ) d a = =  E E 2 0 2 [ ( cos sin )]d 8 2 l z x y a        − − + =     e e e 0 ( 2) 8 2 l z x a    e e − 2.7 三根长度均为 L ，均匀带电荷密度分别为 l1、l 2 和 l3 地 线电荷构成等边三角形。设 l1 = 2 2l = 3 2l ，计算三角形中心处的 电场强度。 解 建立题 2.7 图所示的坐标系。三角形中心到各边的距离为 3 tan 30 2 6 L d L = = 则 1 1 1 0 0 3 (cos30 cos150 ) 4 2 l l y y d L     E e e = − = 2 1 2 0 0 3 3 ( cos30 sin 30 ) ( 3 ) 2 8 l l x y x y L L     E e e e e = − + = − + 3 1 3 0 0 3 3 ( cos30 sin 30 ) ( 3 ) 2 8 l l x y x y L L     E e e e e = − = − 故等边三角形中心处的电场强度为 a z x y dl  l P dE r r 题 2.6 图 l 2 l1 l3 x y o E1 E2 E3 题 2.7 图

E=E+E2+E,= 6-e5+e脸+e5-e2=6 3p1 2.8一点电荷+g位于(-a,0,0)处，另-点电荷-2g位于(a,0,0)处，空间有没有电场强 度E=0的点？ 解电荷+q在(x,y,)处产生的电场为 g e,(x+a)+e,y+e.z E=4x+a2+y+ 电荷-2g在(x,八，)处产生的电场为 E2=- 2q e,(x-a)+e,y+e.: 4π6【x-a)}'+y2+z2T形 (化，y)处的电场则为E=E+E。令E=0,则有 e,(x+a)+e,y+e.=2[e,(x-a)+e,y+e.=] 由上式两对度分量可7-0+ (x+ax-a2+y2+z2]p=2(x-a[x+a2+y2+z2]9 ① [x-a2+y2+22=2x+a+y2+2] ® x-a)}2+y2+2]p=2x+a)+y2+2]2 当y≠0或z≠0时，将式②或式③代入式①，得a=0。所以，当y≠0或：≠0时无解： 当y=0且z=0时，由式①，有 (x+a)(x-a)3=2(x-ax+a)3 解得 x=(-3±2√2)a 但x=-3a+2√2a不合题意，故仅在(-3a-2W2a,0,0)处电场强度E=0。 2.9一个很薄的无限大导电带电面，电荷面密度为0。证明：垂直于平面的：轴上：=：6处 的电场强度E中，有一半是有平面上半径为√3：。的圆内的电荷产生的。 解半径为r、电荷线密度为P,=σdr的带电细圆环在z轴上z=2o处的电场强度为 dE-e.26 故整个导电带电面在z轴上：=：。处的电场强度为 E=e+-e远r+网ea 而半径为√3：，的圆内的电荷产生在：轴上：=。处的电场强度为 20 题2.10图

E E E E = + + = 1 2 3 1 1 1 000 3 3 3 ( 3 ) ( 3 ) 2 8 8 l l l y x y x y LLL       e e e e e − + + − = 1 0 3 4 l y L   e 2.8 －点电荷 +q 位于 ( ,0,0) −a 处，另－点电荷 −2q 位于 ( ,0,0) a 处，空间有没有电场强 度 E = 0 的点？ 解 电荷 +q 在 ( , , ) x y z 处产生的电场为 1 2 2 2 3 2 0 ( ) 4 [( ) ] x y z q x a y z  x a y z + + + = + + + e e e E 电荷 −2q 在 ( , , ) x y z 处产生的电场为 2 2 2 2 3 2 0 2 ( ) 4 [( ) ] x y z q x a y z  x a y z − + + = − − + + e e e E ( , , ) x y z 处的电场则为 E E E = +1 2 。令 E = 0 ，则有 2 2 2 3 2 ( ) [( ) ] x y z x a y z x a y z + + + = + + + e e e 2 2 2 3 2 2[ ( ) ] [( ) ] x y z x a y z x a y z − + + − + + e e e 由上式两端对应分量相等，可得到 2 2 2 3 2 2 2 2 3 2 ( )[( ) ] 2( )[( ) ] x a x a y z x a x a y z + − + + = − + + + ① 2 2 2 3 2 2 2 2 3 2 y x a y z y x a y z [( ) ] 2 [( ) ] − + + = + + + ② 2 2 2 3 2 2 2 2 3 2 z x a y z z x a y z [( ) ] 2 [( ) ] − + + = + + + ③ 当 y  0 或 z  0 时，将式②或式③代入式①，得 a = 0 。所以，当 y  0 或 z  0 时无解； 当 y = 0 且 z = 0 时，由式①，有 3 3 ( )( ) 2( )( ) x a x a x a x a + − = − + 解得 x a = −  ( 3 2 2) 但 x a a = − + 3 2 2 不合题意，故仅在 ( 3 2 2 ,0,0) − −a a 处电场强度 E = 0。 2．9 一个很薄的无限大导电带电面，电荷面密度为  。证明：垂直于平面的 z 轴上 0 z = z 处 的电场强度 E 中，有一半是有平面上半径为 0 3z 的圆内的电荷产生的。 解 半径为 r 、电荷线密度为 d l  = r 的带电细圆环在 z 轴上 0 z = z 处的电场强度为 0 2 2 3 2 0 0 d d 2 ( ) z r z r r z   = + E e 故整个导电带电面在 z 轴上 0 z = z 处的电场强度为 0 0 2 2 3 2 2 2 1 2 0 0 0 0 0 0 0 d 1 2 ( ) 2 ( ) 2 z z z r z r z r z r z         = = − = + +  E e e e 而半径为 0 3z 的圆内的电荷产生在 z 轴上 0 z = z 处的电场强度为 0 0 3 3 0 0 2 2 3 2 2 2 1 2 0 0 0 0 0 0 0 d 1 1 2 ( ) 2 ( ) 4 2 z z z z z r z r z r z r z        = = − = = + +  E e e e E  a Q  b z o dI 题 2.10 图

2.10一个半径为α的导体球带电荷量为Q,当球体以均匀角速度。绕一个直径旋转，如题 2.10图所示。求球心处的磁感应强度B。 解球面上的电荷面密度为 64d2 0 当球体以均匀角速度o绕一个直径旋转时，球面上位置矢量r=e,a点处的电流面密度为 Js=ov=goxr=geoxea= egan0=6品a0 将球面划分为无数个宽度为dl=ad0的细圆环，则球面上任一个宽度为dl=ad0细圆环 的电流为 d1=Jsdl=esinode A 细圆环的半径为b=asin@,圆环平面到球心的距离d=acos0,利用电流圆环的轴线上的磁 场公式，则该细圆环电流在球心处产生的磁场为 4,b2d1 uoOa'sin0d0 dB-e:de:8md sin 0 cos=e.sin0do 8πa 常 电流！以相同的方向流过这两个线圈。 (1)求这两个线圈中心点处的磁感应强度B=e,B: (2)证明：在中点处dB/dx等于零： (3)求出b与d之间的关系，使中点处d2B,/dx2也等于零。 解(1)由细圆环电流在其轴线上的磁感应强度 4,la2 B=6:2a2+2 得到两个线圈中心点处的磁感应强度为 HoNIb2 B=6,6+4 (2)两线圈的电流在其轴线上x(0<x<d)处的磁感应强度为 4W7b2 4W7b2 B=e,26+x西+2b+d-xr 所以 3toNIb2x ,34Nb2(d-x) 0Bx二一2(b2+x2)22b2+(d-x)273 dx 故在中点x=d2处，有 dB:= 34N7b2d/2,34,N7b2d/2 dr26+d40+26+dr4=0 题2.11图

2.10 一个半径为 a 的导体球带电荷量为 Q ，当球体以均匀角速度  绕一个直径旋转，如题 2.10 图所示。求球心处的磁感应强度 B 。 解 球面上的电荷面密度为 2 4 Q a   = 当球体以均匀角速度  绕一个直径旋转时，球面上位置矢量 r r e = a 点处的电流面密度为 S z r J v = =  =  =     ω r e e a sin sin 4 Q a a        e e = 将球面划分为无数个宽度为 d d l a =  的细圆环，则球面上任一个宽度为 d d l a =  细圆环 的电流为 d d sin d 4 S Q I J l     = = 细圆环的半径为 b a = sin ，圆环平面到球心的距离 d a = cos ，利用电流圆环的轴线上的磁 场公式，则该细圆环电流在球心处产生的磁场为 2 0 2 2 3 2 d d 2( ) z b I b d  = = + B e 2 3 0 2 2 2 2 3 2 sin d 8 ( sin cos ) z Qa a a        = + e 3 0 sin d 8 z Q a      e 故整个球面电流在球心处产生的磁场为 3 0 0 0 sin d 8 6 z z Q Q a a          = =  B e e 2.11 两个半径为 b 、同轴的相同线圈，各有 N 匝，相互隔开距离为 d ，如题 2.11 图所示。 电流 I 以相同的方向流过这两个线圈。 （1）求这两个线圈中心点处的磁感应强度 B e = x x B ； （2）证明：在中点处 d d B x x 等于零； （3）求出 b 与 d 之间的关系，使中点处 2 2 d B d x x 也等于零。 解 （1）由细圆环电流在其轴线上的磁感应强度 2 0 2 2 3 2 2( ) z Ia a z  = + B e 得到两个线圈中心点处的磁感应强度为 2 0 2 2 3 2 ( 4) x NIb b d  = + B e （2）两线圈的电流在其轴线上 x (0  x  d) 处的磁感应强度为 2 2 0 0 2 2 3 2 2 2 3 2 2( ) 2[ ( ) ] x NIb NIb b x b d x     = +     + + − B e 所以 2 2 0 0 2 2 5 2 2 2 5 2 d 3 3 ( ) d 2( ) 2[ ( ) ] B NIb x NIb d x x x b x b d x   − = − + + + − 故在中点 x = d 2 处，有 2 2 0 0 2 2 5 2 2 2 5 2 d 3 2 3 2 0 d 2[ 4] 2[ 4] B NIb d NIb d x x b d b d   = − + = + + b I b I d 题 2.11 图 x

(3) d2B154N7b2x234N7b2 dx262+x)26+x)0+ 154,N7b2(d-x)2 34,Wb2 26+(d-x而-26+(d-xy丽 令d 1 dr2=0,有 5d2/4 b+d4丽b+d4=0 即 5d2/4=b2+d2/4 故解得 d=b 2.12一条扁平的直导体带，宽为2a,中心线与：轴重合，通过的电流为1。证明在第一 象限内的磁感应强度为 8=一a,8-品n 式中0、5和5如题2.12图所示。 dB 解将导体带划分为无数个宽度为dx'的细条带，每一 (x) 细条带的电流山=名，由安掉环路定理，可得位于？处 的细条带的电流d!在点P(x,y)处的磁场为 dB=dIdx Hol dx' Andl(x-x+y 则 dB,=-dBsin= uolydx' 4πd(x-x)2+y2] 题2.12图 dB.=dBcos0= ol(x-x)dx' 4πa(x-x)2+y2] 所以 uolydx' y儿- 41 -a-x） 41 4π arctana-x (y arctany 2-4元a arctan (y a,-a)=-4ra 4πa 8兴兰总岭 uol(x-x)dx' 2.13如题2.13图所示，有一个电矩为的电偶极子，位于坐标原点上，另一个电矩为2的 电偶极子，位于矢径为”的某一点上。试证明两偶极子之间相互作用力为 E-器mA如风o4-2o8ca4)

（3） 2 2 2 2 0 0 2 2 2 7 2 2 2 5 2 d 15 3 d 2( ) 2( ) B NIb x NIb x x b x b x   = − + + + 2 2 2 0 0 2 2 7 2 2 2 5 2 15 ( ) 3 2[ ( ) ] 2[ ( ) ] NIb d x NIb b d x b d x   − − + − + − 令 0 d d 2 2 2 x=d = x x B ，有 0 [ 4] 1 [ 4] 5 4 2 2 7 2 2 2 5 2 2 = + − b + d b d d 即 5 4 4 2 2 2 d = b + d 故解得 d = b 2.12 一条扁平的直导体带，宽为 2a ，中心线与 z 轴重合，通过的电流为 I 。证明在第一 象限内的磁感应强度为 0 4 x I B a    = − ， 0 2 1 ln 4 y I r B a r   = 式中  、1 r 和 2 r 如题 2.12 图所示。 解 将导体带划分为无数个宽度为 d x  的细条带，每一 细条带的电流 x a I I = d  2 d 。由安培环路定理，可得位于 x  处 的细条带的电流 dI 在点 P(x, y) 处的磁场为 0 0 d d d 2 4 I I x B R aR      = = = 0 2 2 1 2 d 4 [( ) ] I x a x x y    − +  则 0 2 2 d d d sin 4 [( ) ] x Iy x B B a x x y     = − = − − +  0 2 2 ( )d d d cos 4 [( ) ] y I x x x B B a x x y    −   = = − +  所以 0 2 2 d 4 [( ) ] a x a Iy x B a x x y   −  = − = − +   0 arctan 4 a a I x x a y   −    − − =     0 arctan arctan 4 I a x a x a y y         − − − − − =             0 arctan arctan 4 I x a x a a y y         + − − − =             0 2 1 ( ) 4 I a     − − = 0 4 I a    − 0 2 2 ( )d 4 [( ) ] a y a I x x x B a x x y   − −   = = − +   0 2 2 ln[( ) ] 8 a a I x x y a   − − − + =  2 2 0 2 2 ( ) ln 8 ( ) I x a y a x a y   + + = − + 0 2 1 ln 4 I r a r   2.13 如题 2.13 图所示，有一个电矩为 1 p 的电偶极子，位于坐标原点上，另一个电矩为 2 p 的 电偶极子，位于矢径为 r 的某一点上。试证明两偶极子之间相互作用力为 1 2 4 1 2 1 2 0 3 (sin sin cos 2cos cos ) 4 r p p F r        = − −a a I x y 2 r 1 r P(x, y) d B R  1 2 题 2.12 图