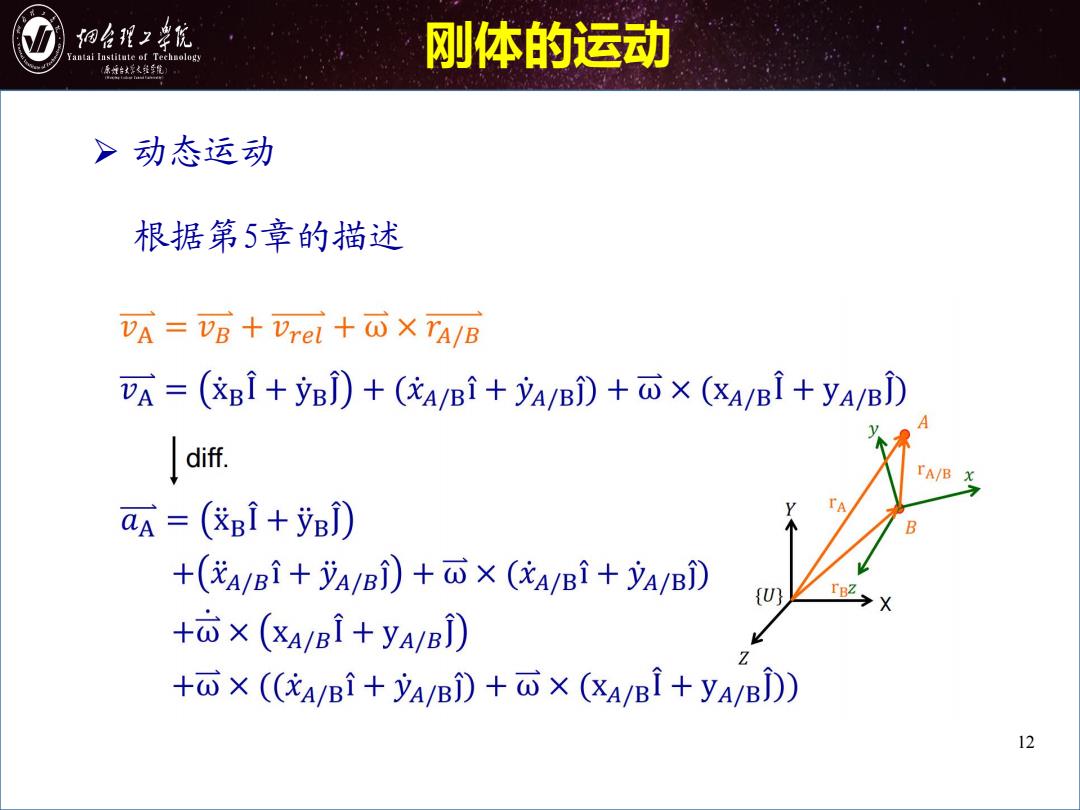
细台形2幸院 antai Institute of Technology 刚体的运动 原城台好火维年馆 》动态运动 根据第5章的描述 VA=VB+Vrel+西XTA/B A=(区Bi+yB)+(A/Bi+yA/Bi)+石×(&4/B1+yA/B) diff. TA/B x aA=(&知1+yB) +(花A/Bi+yA/Bj)+云X(A/Bi+yA/B) +六×(&A/Bi+yAyB) +×(A/Bi+yA/Bi)+瓜X(&ABl+yA/BD) 12
12 刚体的运动 Ø 动态运动 根据第5章的描述

细台形z幸优 antai Institute of Technology 刚体的运动 原城台好火维年航 aA=(BI+BJ) +六×(&A/B1+yA/B)+云×(⑥×(&A/B1+yA/BD) +2而×(A/Bi+yA/B)+(xA/Bi+yA/Bj) aA=aB+云×a/B+而X西XTA/B +20 X Vrel arel TA/B x 科氏加速度 相对加速度 {B) >因此 (4) X AAQ=AAB ORG Z +AnB×RBPo+AnB×(A2B×RBPa) +2A2B×8RBVg+8RBAg 13
13 刚体的运动 科氏加速度 相对加速度 Ø 因此

细台形z幸院 antai Institute of Technology 质量分布 原城台好火维年院 >相对于坐标系{A}的惯性张量 一1x -Ixz {A} 小2 A1= w -lyz dv 1yz Izz 惯性矩 惯性积 Les=y2+zodv a=狐pn y=瓜e2+2o a=瓜 xzpdv a=∬cx2+ypd 0 a=肌ygnn 14
14 质量分布 Ø 相对于坐标系{A}的惯性张量 惯性矩 惯性积

细台程2幸优 antai Institute of Technology 质量分布 原城台好火维年馆 >惯性张量 ◆实常数对称矩阵(可以正交对角化) 它的特征分解(也就是M=VAV-1) Ixx -Ixz 0 AI= Ixy l -lyz =R w RT -Ixz -lyz 12z l0 主惯性矩 旋转矩阵,揭示了 主轴的方向 Ixx +lyy +Izz trace(AI)constant ●迹在相似变换下是不变的 ◆如果xy平面是对称平面,则Ixz=Iyz=0 15
15 质量分布 Ø 惯性张量 主惯性矩 u实常数对称矩阵(可以正交对角化) 它的特征分解(也就是 ) 旋转矩阵,揭示了 主轴的方向 u l 迹在相似变换下是不变的 u如果xy平面是对称平面,则

细台程2幸优 antai Institute of Technology 质量分布 原城台好火维年院 >平行轴原理 ◆计算惯性张量在参考坐标系平移下的变化 Alzz CIzz m(xe2 ye2) C:刚体的重心(C0M) AIxy=CIxy-mxcye A:任意坐标系 ,矩阵向量形式 AI CI+m[PeT Pel3-PePe] Pe=[Xc yc Zc]T 相对于坐标系{A的C0M 16
16 质量分布 Ø 平行轴原理 C:刚体的重心(COM) A:任意坐标系 u计算惯性张量在参考坐标系平移下的变化 u 矩阵向量形式 相对于坐标系{A}的COM