《电路理论》课程教学课件（讲稿）第16章 二端口网络

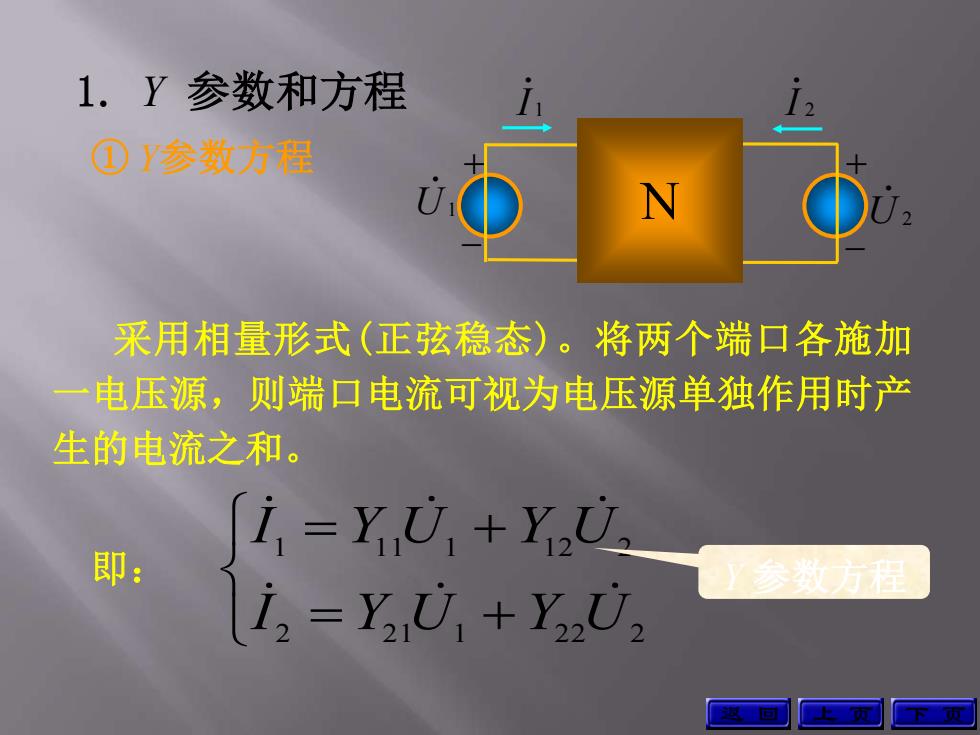
1.Y参数和方程 ①参数方程 N 采用相量形式（正弦稳态）。将两个端口各施加 电压源，则端口电流可视为电压源单独作用时产 生的电流之和。 i=yU,+Y立 即： 参数方 i,=YU+YU

1. Y 参数和方程 采用相量形式(正弦稳态)。将两个端口各施加 一电压源，则端口电流可视为电压源单独作用时产 生的电流之和。 即：        2 2 1 1 2 2 2 1 1 1 1 1 2 2 I Y U Y U I Y U Y U       Y 参数方程 ① Y参数方程 上 页 下 页 +  2  I 2  U +  1  U 1  I N 返 回

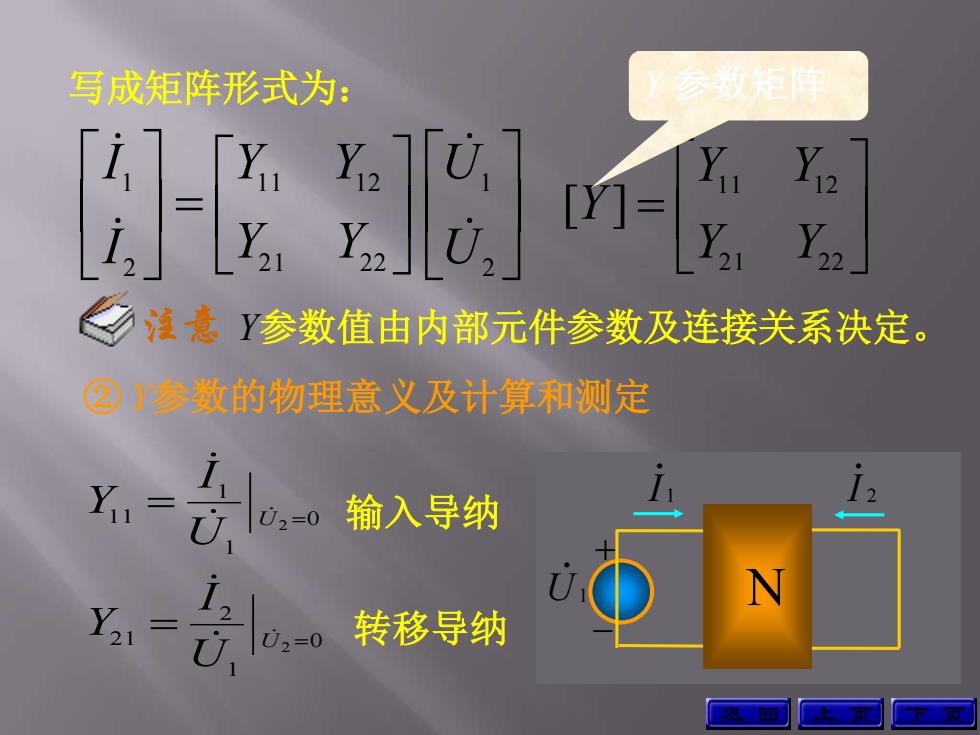
写成矩阵形式为： 参数矩陶 注意参数值由内部元件参数及连接关系决定。 ②Y参数的物理意义及计算和测定 输入导纳 N Y= 转移导纳

写成矩阵形式为：                    2 1 2 1 2 2 1 1 1 2 2 1 U U Y Y Y Y I I            21 22 11 12 [ ] Y Y Y Y Y Y参数值由内部元件参数及连接关系决定。 Y 参数矩阵 ② Y参数的物理意义及计算和测定 0 1 2 21 0 1 1 11 2 2     U U U I Y U I Y       输入导纳 转移导纳 上 页 下 页 注意 +  2  I 2  U +  1  U 1  I N 2  I +  1  U 1  I N 返 回

N Y= i 01=0 转移导纳 01=0 输入导纳 Y→ 短路导纳参数 回

0 2 2 22 0 2 1 12 1 1     U U U I Y U I Y       转移导纳 输入导纳 Y → 短路导纳参数 上 页 下 页 +  2  I 2  U +  1  U 1  I N +  2  I 2  U 1  I N 返 回

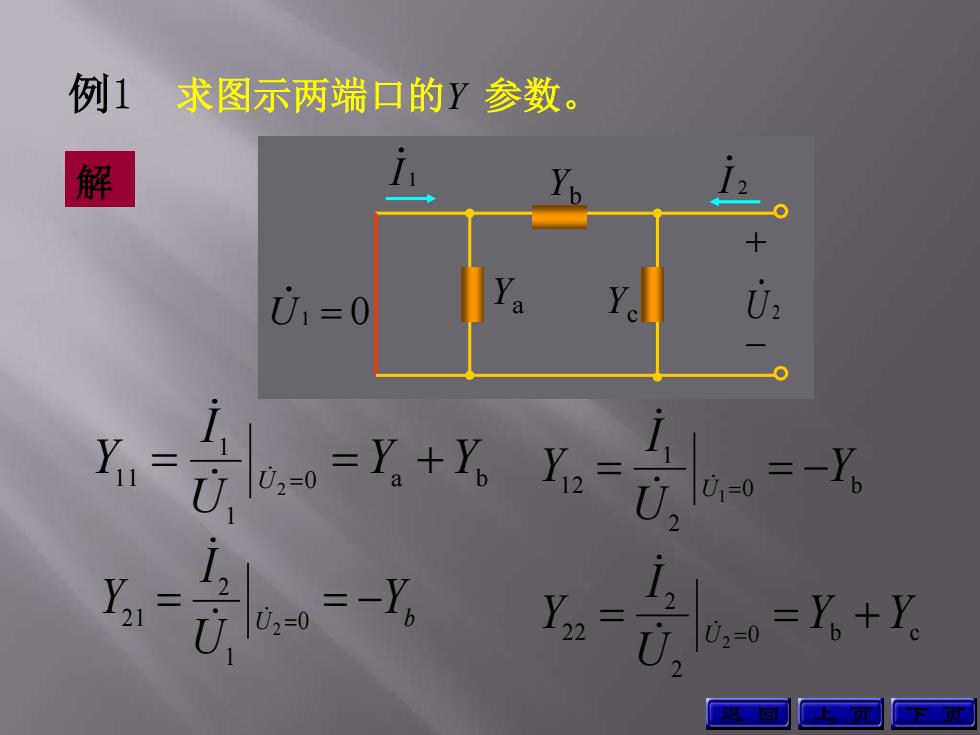
例1 求图示两端口的Y参数。 解 01=0 I c Xi=

例1 0 a b 1 1 1 1 2 Y Y U I Y U        U Yb U I Y    0 1 2 21 2    解 0 b c 2 2 2 2 0 b 2 1 1 2 2 1 Y Y U I Y Y U I Y U U               求图示两端口的Y 参数。 上 页 下 页 1  U 2  I 1  I Yb +  +  2  U Ya Yc 1  U 2  I 1  I Yb +  Ya Yc 2  0  U 1  0  U 2  I 1  I Yb +  Ya Yc 2  U 返 回

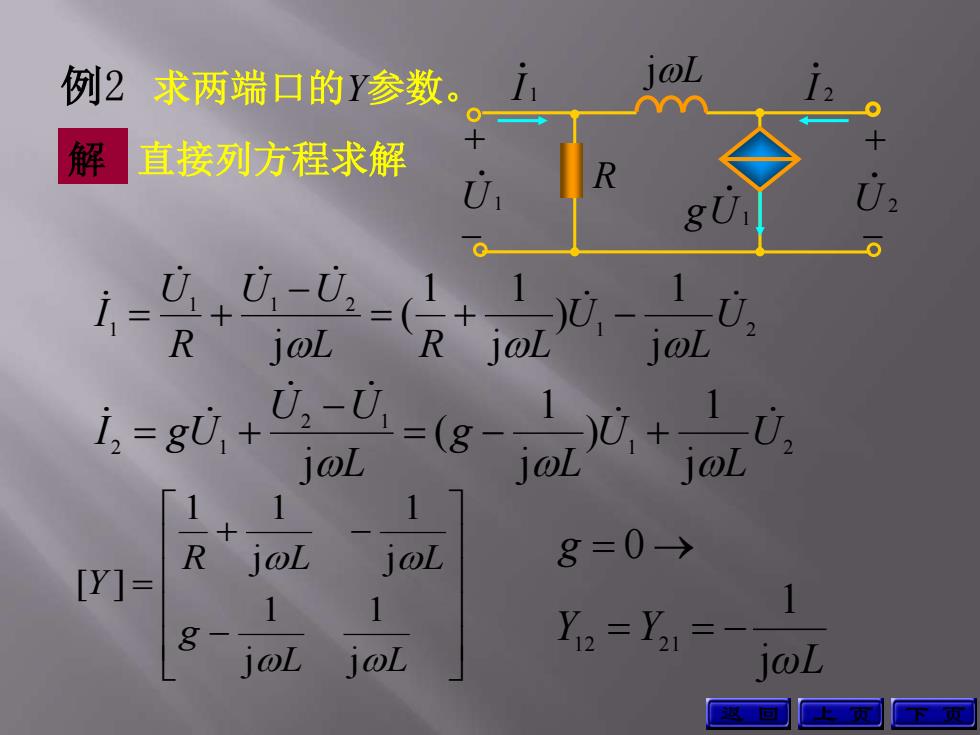
例2求两端口的Y参数。i 10L 解 直接列方程求解 U R g R joL joL 1 1 1 R joL joL 8=0→ [Y]= 1 1 8- joL joL i@L 回

例2 1 2 1 1 2 1 j 1 ) j 1 1 ( j U L U L R L U U R U I                解 直接列方程求解 1 2 2 1 2 1 j 1 ) j 1 ( j U L U L g L U U I gU                                L L g R L L Y     j 1 j 1 j 1 j 1 1 [ ] ωL Y Y g j 1 0 12  21     上 页 下 页 求两端口的Y参数。 jL +  +  1  U 1  I 2  I 2  U R 1  gU 返 回