
③互易二端口(满足互易定理, 当U=心,时,i,=i, 12 上例中有 Y2=Y1=-Y 乡注意互易二端口四个参数中只有三个是独立的
0 2 1 12 1 U U I Y 0 1 2 21 2 U U I Y 1 2 1 2 U U , I I 当 时 Y1 2 Y2 1 上例中有 Y12 Y21 Yb 互易二端口四个参数中只有三个是独立的。 ③互易二端口(满足互易定理) 上 页 下 页 注意 返 回

④对称二端口 对称二端口F 除Y2=Y外,还满足Y=Y2, 上例中,Y。Y。=Y时,Y1=Y22=Y+Y 乡注意对称二端口只有两个参数是独立的。 对称二端口是指两个端口电气特性上对称。 电路结构左右对称的一般为对称二端口。.结构不 对称的二端口,其电气特性可能是对称的,这样 的二端口也是对称二端口
上例中,Ya =Yc =Y 时, Y11 =Y22 =Y+ Yb 对称二端口只有两个参数是独立的。 对称二端口是指两个端口电气特性上对称。 电路结构左右对称的一般为对称二端口。结构不 对称的二端口,其电气特性可能是对称的,这样 的二端口也是对称二端口。 ④对称二端口 , , 对称二端口 除Y12 Y21外 还满足Y11 Y22上 页 下 页 注意 返 回
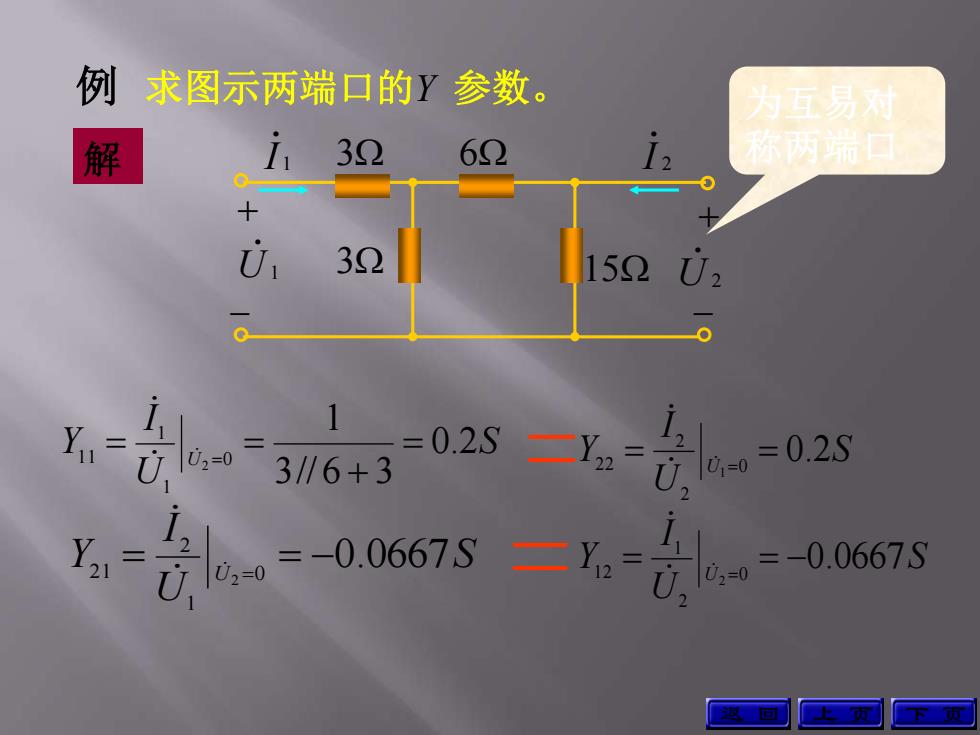
例求图示两端口的Y参数。 为互易对 解 i32 62 称两端门 0 + 0, 32 15202 0 Yu= 02=0 =0.2S 3∥6+3 -2=02 Y2
例 解 S U I Y U 0.2 3// 6 3 1 0 1 1 1 1 2 S U I Y U 0.0667 0 1 2 2 1 2 S U I Y S U I Y U U 0.0667 0.2 0 2 1 1 2 0 2 2 2 2 2 1 上 页 下 页 求图示两端口的Y 参数。 3 6 3 15 + + 1 U 1 I 2 I 2 U 为互易对 称两端口 返 回
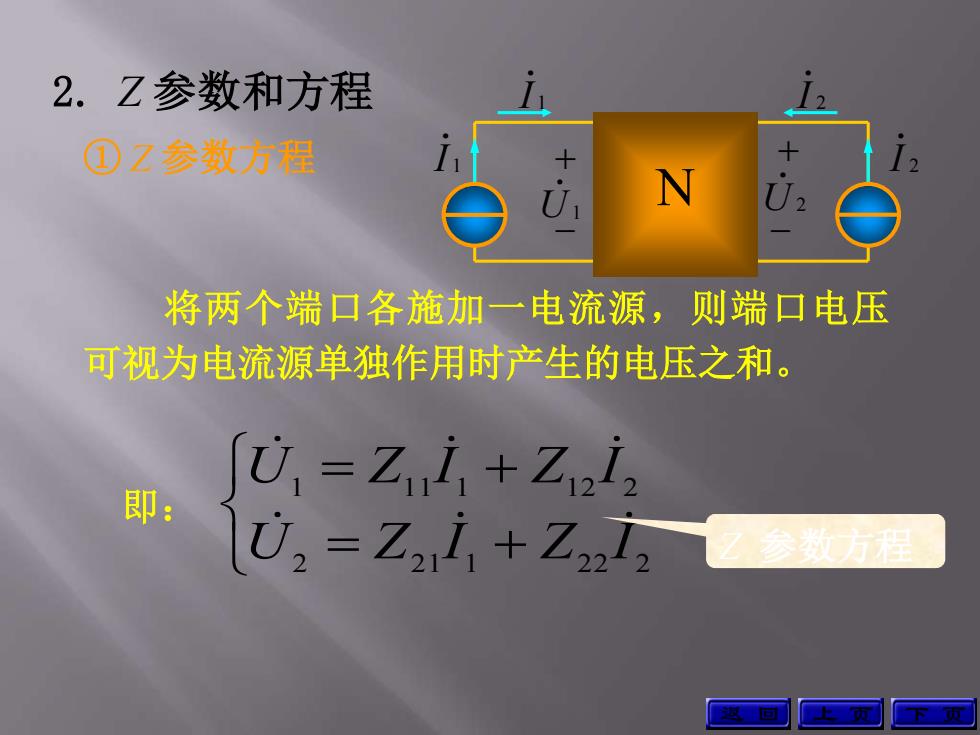
2.Z参数和方程 ①☑参数方程 将两个端口各施加一电流源,则端口电压 可视为电流源单独作用时产生的电压之和。 U=Zi+Zi 即: 1U,=Z2,1+Z2122参数通
2. Z 参数和方程 将两个端口各施加一电流源,则端口电压 可视为电流源单独作用时产生的电压之和。 即: 2 2 1 1 2 2 2 1 1 1 1 1 2 2 U Z I Z I U Z I Z I Z 参数方程 ① Z 参数方程 返 回 上 页 下 页 + 2 I 2 U + 1 U 1 I N 1 I 2 I

也可由Y参数方程 i,=YU1+Y,02 解出), i,=yU,+Y02 即: -大-1 +-21+21 得到Z参数方程。其中△=Y2-21 其矩阵形式为: 卧-
也可由Y 参数方程 2 21 1 22 2 1 11 1 12 2 I Y U Y U I Y U Y U . 1 U2 U , 解出 2 2 1 1 2 2 2 1 1 1 2 1 2 2 1 1 1 1 2 2 1 2 1 2 2 1 I Z I Z I Y I Y U I Z I Z I Y I Y U 即: 得到Z 参数方程。其中 =Y11Y22 –Y12Y21 其矩阵形式为: 2 1 2 1 2 1 2 2 1 1 1 2 2 1 I I Z I I Z Z Z Z U U 返 回 上 页 下 页