
Boltzmann方程的理解: 左边两项称漂移项(drift term), 右边的项称为碰撞项(collision term)或散射项(scattering) 按照半经典模型: 点-u国-清,E网 =F=-e[EG,0+迈,(×BC,0] dt Bolt忆mann方程就是从能带结构出发,利用这些关系,将 碰撞的作用与分布函数相联系,成为处理固体中输运现 象的出发点
Boltzmann方程的理解: 左边两项称漂移项(drift term), 右边的项称为碰撞项(collision term)或散射项(scattering) 按照半经典模型: d 1 ( ) ( ) d d ( , ) ( ) ( , ) d n k n n r k E k t k F e E r t k B r t t u u = = Ñ = = - é ù + ´ ë û v v v v h v v v v v v v v h Boltzmann方程就是从能带结构出发,利用这些关系,将 碰撞的作用与分布函数相联系,成为处理固体中输运现 象的出发点
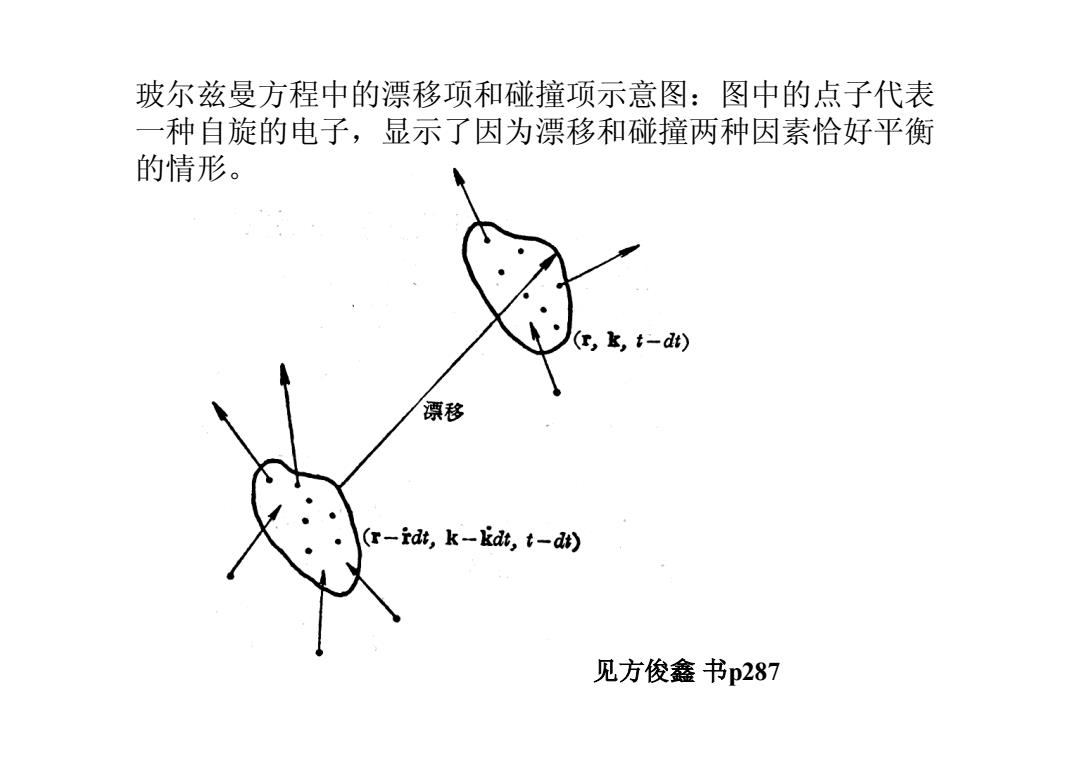
玻尔兹曼方程中的漂移项和碰撞项示意图:图中的点子代表 一种自旋的电子,显示了因为漂移和碰撞两种因素恰好平衡 的情形。 (r,k,t-dt) 漂移 (r-idt,k-kdt,t-dt) 见方俊鑫书p287
玻尔兹曼方程中的漂移项和碰撞项示意图:图中的点子代表 一种自旋的电子,显示了因为漂移和碰撞两种因素恰好平衡 的情形。 见方俊鑫 书p287

下面我们讨论一维定态的导电问题时(比如一根均匀 导线内的情形),分布函数和位置r无关,第一项为零, 又因为: dk es 是电场强度 dt h 玻尔兹曼方程可以简化为: &7.f(k)=b-a 简化后,玻尔兹曼方程仍是一个微分积分方程,碰 撞项(b-)的积分中还包含有未知的分布函数,在一 般情况下,该方程得不到简单的解析形式解,要采用近似 方法才行。(关键是碰撞项的积分求解困难很大)
下面我们讨论一维定态的导电问题时(比如一根均匀 导线内的情形),分布函数和位置 r 无关,第一项为零, 又因为: d d k e t e = - h 玻尔兹曼方程可以简化为: ( ) k e - eÑ f k = -b a h 简化后,玻尔兹曼方程仍是一个微分-积分方程,碰 撞项( b – a )的积分中还包含有未知的分布函数,在一 般情况下,该方程得不到简单的解析形式解,要采用近似 方法才行。(关键是碰撞项的积分求解困难很大) e 是电场强度

7.2弛豫时间近似和电导率公式: (参考黄昆书6.4节p296) 一个广泛应用的近似方法是弛豫时间近似,碰撞项可以 表示为: af(r,k.t) =b-a=--6 τ(k) 其中:f6为处于平衡态时的Fermi一Dirac2分布函数, τ(k)是引入的参量,定义为弛豫时间,是k的函数。 这个假设的根据是考虑到碰撞促使系统趋于平衡态的 特点。若系统原来不平衡,即t=0时,f=f+△f(t=0), 在=0时撤去外场,若只有碰撞作用时,对平衡的偏离 △(t=O)应很快消失。关于弛豫时间近似的假设认为,碰 撞促使对平衡分布的偏差是以指数的形式消失,因为,只 有碰撞时: 对-f-0 8t
7.2 弛豫时间近似和电导率公式: 0 coll ( , , ) ( ) f r k t f f b a t k t æ ö ¶ - ç ÷ = - = - è ø ¶ v 一个广泛应用的近似方法是弛豫时间近似,碰撞项可以 表示为: 其中: f0 为处于平衡态时的Fermi-Dirac分布函数, t (k) 是引入的参量,定义为弛豫时间,是 k 的函数。 这个假设的根据是考虑到碰撞促使系统趋于平衡态的 特点。若系统原来不平衡,即 t = 0时, f = f0+Df (t = 0), 在 t = 0 时撤去外场,若只有碰撞作用时, 对平衡的偏离 Df (t = 0)应很快消失。关于弛豫时间近似的假设认为,碰 撞促使对平衡分布的偏差是以指数的形式消失,因为,只 有碰撞时: 0 f f f t t ¶ - = - ¶ (参考黄昆书6.4节p296)

对t积分得到的解是: 0=-=u=0jep 所以,弛豫时间τ大致就是系统恢复平衡所用的时间。 于是,Boltzmann方程可简化为 /=- T 这个方程的解就是在电场ε存在时定态的分布函数∫。 可以认为非平衡的稳态分布相对于平衡分布偏离很小, ∫=+f 这里是一个小量,采用一级近似 上试简化为:务e=- T
对 t 积分得到的解是: ( ) ( ) ( ) 0 0 exp t t f t f f f t t æ ö D = - = D = -ç ÷ è ø 所以,弛豫时间 t 大致就是系统恢复平衡所用的时间。 于是,Boltzmann方程可简化为 0 ( ) e f f e f k t - - ×Ñ = - h k 这个方程的解就是在电场 e 存在时定态的分布函数 f 。 可以认为非平衡的稳态分布相对于平衡分布偏离很小, 0 1 f = + f f 上式简化为: 这里 f 1 是一个小量,采用一级近似 1 0 ( ) e f e f k t - ×Ñ = - h k