
解:导体球的电导率一般总是远大于土壤的电导率,可将 导体球看作等位体。用静电比拟法,位于电介质中的半径 为a的导体球的电容为 C=4π8m 所以导体球的接地电导为 G=4π 接地电阻为 1 R= 4π0u
解:导体球的电导率一般总是远大于土壤的电导率,可将 导体球看作等位体。用静电比拟法,位于电介质中的半径 为a的导体球的电容为 C = 4a 所以导体球的接地电导为 G = 4a 接地电阻为 G a R 4 1 1 = =

3.2磁感应强度 在运动电荷的周围,除了电场,还存在一种称为 磁场的物质。 •描述磁场特性的基本物理量:磁感应强度B •磁场的表现:对于引入场中的运动电荷有力的作 用。如电荷q以速度V运动,磁场对其对作用力为 f=q(ixB) 磁场对运动电荷的作用力又称洛仑兹力。洛仑兹 力不能做功。通有电流的导线元d在磁场中,此 时这个电流元(Id)所受到的力 df dqv x B=Idl x B
B v •在运动电荷的周围,除了电场,还存在一种称为 磁场的物质。 •描述磁场特性的基本物理量:磁感应强度 •磁场的表现:对于引入场中的运动电荷有力的作 用。如电荷q以速度 运动,磁场对其对作用力为 f q(v B) = •磁场对运动电荷的作用力又称洛仑兹力。洛仑兹 力不能做功。通有电流I的导线元 在磁场中,此 时这个电流元(I )所受到的力 dl df dqv B Idl B = = 3.2 磁 感 应 强 度 dl
安培定律指出:在真空中载有电流1,的回路C1上任一线元d1对 另一载有电流,的回路C,上任一线元dl,的作用力表示为 C af。=xU叫xR 4元 R3 -王 Idl2×(Idl×R) R3 Ef成” 安培定律
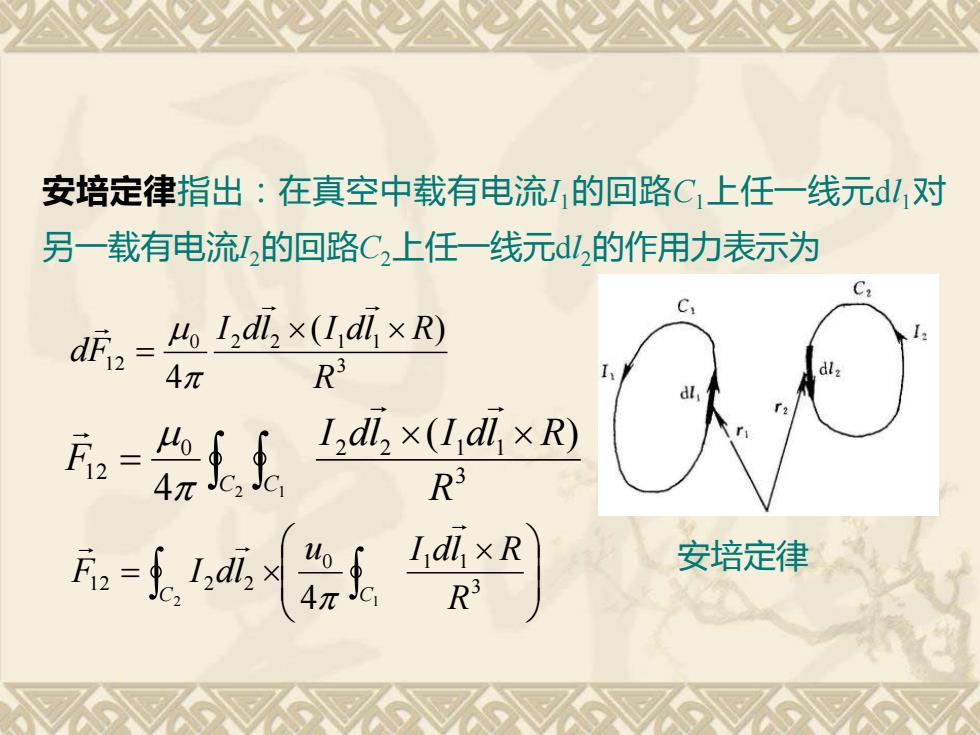
安培定律指出:在真空中载有电流I1的回路C1上任一线元dl1对 另一载有电流I2的回路C2上任一线元dl2的作用力表示为 3 0 2 2 1 1 1 2 ( ) 4 R I dl I dl R dF = 3 0 2 2 1 1 1 2 ( ) 4 2 1 R I dl I dl R F C C = = 3 0 1 1 1 2 2 2 2 4 1 R u I dl R F I dl C C 安培定律

令 B=Mo Idl xR 4πJ R3 若电流不是线电流,而是具有体分布的电流J,则有 01 =会1公8 dF Idl x B
令 = 1 3 0 1 1 4 C R I dl R B 若电流不是线电流,而是具有体分布的电流J,则有 ' ( ') 4 ( ) 3 0 dV R J r R B r V = ' ( ') 4 ( ) 3 0 dS R J r R B r S S = dF Idl B =

可以用上式计算各种形状的载流回路在外磁场中受到的力和力 矩。 对以速度V运动的点电荷q,其在外磁场B中受的力是 F=gqD×B 如果空间还存在外电场E,电荷受到的力还要加上电场力。这样 就得到带电以速度运动的点电荷在外电磁场(E,B)中受到的电 磁力为 F=q(E+F×B) 上式称为洛仑兹力公式
可以用上式计算各种形状的载流回路在外磁场中受到的力和力 矩。 F qv B = 如果空间还存在外电场E,电荷q受到的力还要加上电场力。这样, 就得到带电q以速度v运动的点电荷在外电磁场(E,B)中受到的电 磁力为 F q(E v B) = + 上式称为洛仑兹力公式。 对以速度v运动的点电荷q,其在外磁场B中受的力是