2)一阶保持器的传递函数 一阶保持器的脉冲响应函数应该如图8-9所示。 h(t ②单位斜坡 ⑥单位斜坡 2 ①单位阶跃 ⑤单位阶跃 2T T 2T ③2×单位阶趺④2X单位阶跃 图8-9一阶保持器的脉冲响应函数 2023/7124 北科大信息工程学院自动化 26
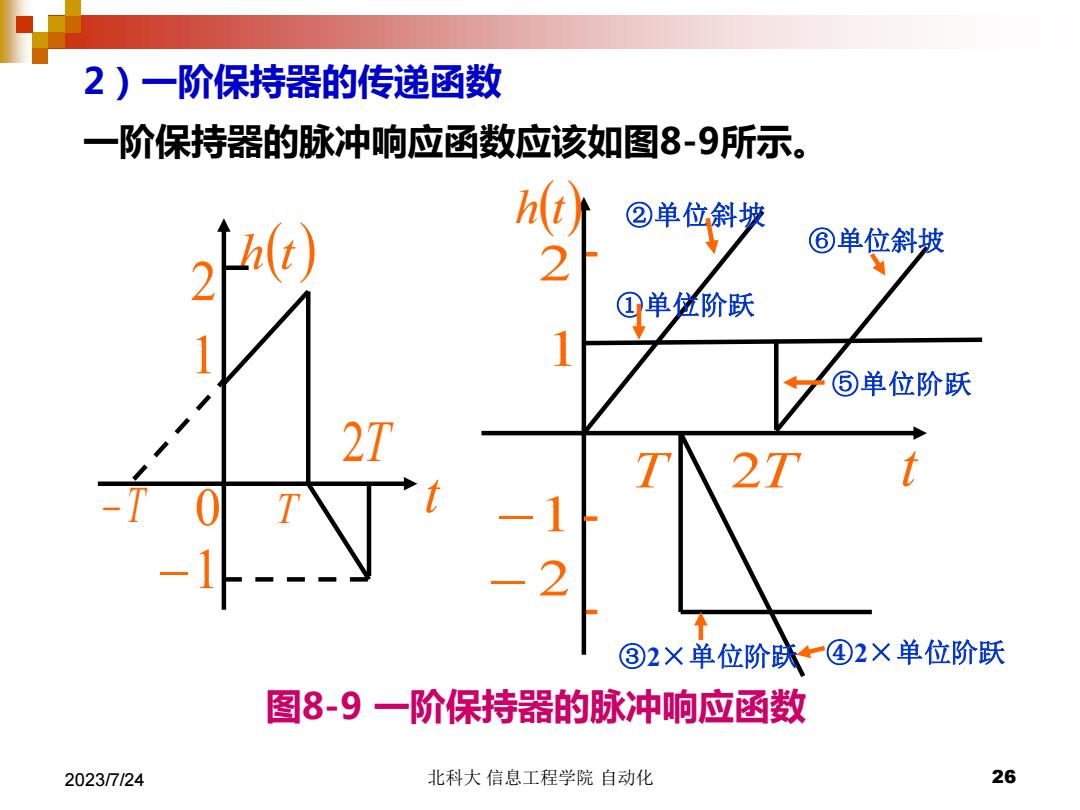
2023/7/24 北科大 信息工程学院 自动化 26 一阶保持器的脉冲响应函数应该如图8-9所示。 h(t) 1 −1 −T 0 T t 2 2T ①单位阶跃 ②单位斜坡 ③2×单位阶跃 ④2×单位阶跃 ⑤单位阶跃 ⑥单位斜坡 −1 − 2 T 2T 1 2 h(t) t 图8-9 一阶保持器的脉冲响应函数 2)一阶保持器的传递函数
根据一阶保持器脉冲响应函数的分解,可得其传递函数: G,)=71+g-e s 3)一阶保持器的频谱分析 实线是一阶保持器幅频特性;虚线为零阶保持器频率特性。 G,0o) 1.0T 20s30s 40s -18d0 -280 ∠G,(jo) 图8-10 保持器的频率特性 20237124 北科大信息工程学院自动化 27
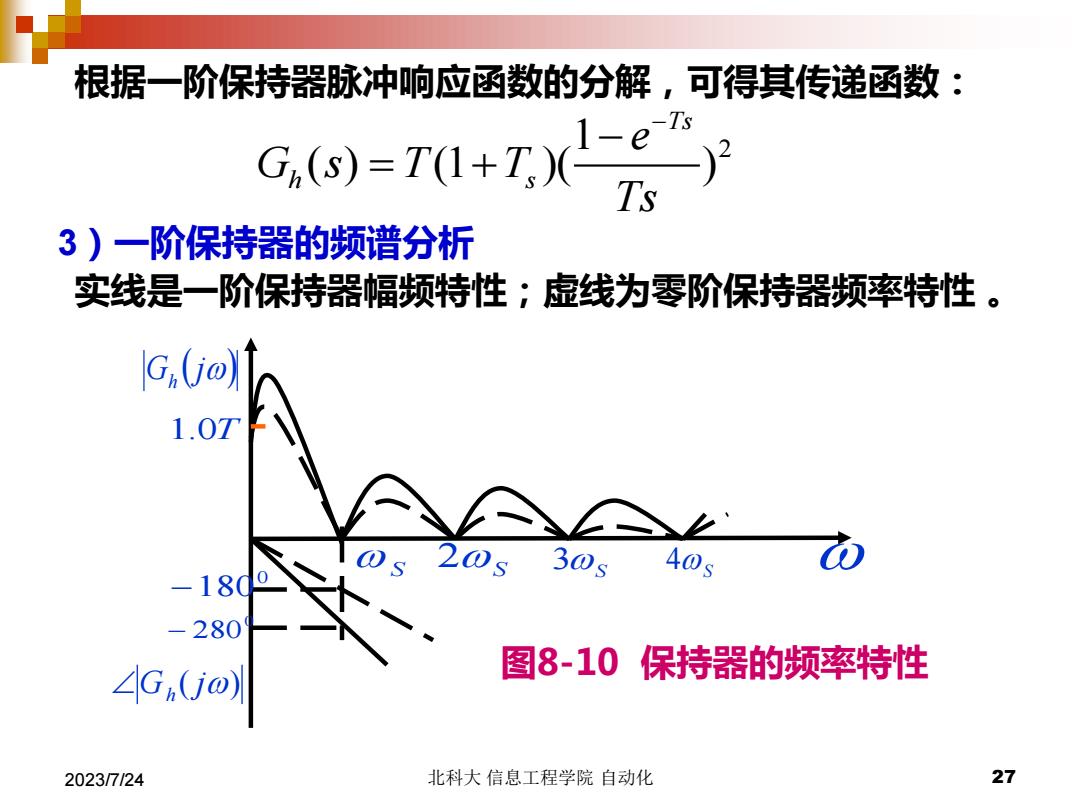
2023/7/24 北科大 信息工程学院 自动化 27 根据一阶保持器脉冲响应函数的分解,可得其传递函数: 1 2 ( ) (1 )( ) Ts h s e G s T T Ts − − = + 3)一阶保持器的频谱分析 实线是一阶保持器幅频特性;虚线为零阶保持器频率特性 。 0 S 2S −180 G ( j) h 3S 0 − 280 G (j) h S 4 1.0T 图8-10 保持器的频率特性

8.4z变换理论及线性差分方程求解 一、定义 二、z变换的性质 三、z变换方法 四、z反变换方法 五、线性差分方程及其求解 2023/7/24 北科大信息工程学院自动化 28
2023/7/24 北科大 信息工程学院 自动化 28 8.4 z变换理论及线性差分方程求解 一、定义 二、 z变换的性质 三、z变换方法 四、z反变换方法 五、线性差分方程及其求解

F(s)LIf(t)]=f(nT)e-mTs 一、定义 n=0 F(z)e∑f(nT)z”=ZLf(t)] n=0 其中f(是连续函数 的采样信号, z=els 采样函数f对应的Z变换是唯一的。Z变换只适用于离 散函数,因为它只表征了连续函数在采样时刻的特性。 Z反变换表示为: ZF(a]=/( 用查表方法可得到函数∫的变换。 20237/24 北科大信息工程学院自动化 29
2023/7/24 北科大 信息工程学院 自动化 29 其中 是连续函数 的采样信号, 一、定义 * 0 ( ) ( ) [ ( )] n n F z f nT z Z f t − = = ( ) * f t f (t) Ts z = e 采样函数 对应的Z 变换是唯一的。Z 变换只适用于离 散函数,因为它只表征了连续函数在采样时刻的特性。 Z反变换表示为: ( ) * f t [ ( )] ( ) 1 * Z F z = f t − 用查表方法可得到函数 ( 的 ) Z变换。 * f t * * 0 ( ) [ ( )] ( ) nTS n F s L f t f nT e − = =

二、 z变换的性质 1) 线性定理 za,x(0)+a2,0+…=a,X(Z))+aX,(Z)+… 式中a1a2,···为常数。 2)实平移定理 x+mD]=zmx()-x(kT) 当k<O时,(kT)成立,则有: z[x(t-mT)]=zmX(z) 2023/7/24 北科大信息工程学院自动化 30
2023/7/24 北科大 信息工程学院 自动化 30 1)线性定理 式中a1 ,a2 , ···为常数。 2) 实平移定理 za1 x1 (t) + a2 x2 (t) + = a1 X1 (Z)+ a2 X2 (Z)+ ( ) ( ) 1 0 ( ) m m K K Z x t mT Z X z x kT z − − = + = − ( ) ( ) m z x t mT z X z − − = 二、 z变换的性质 当k<0时,有 x kT ( ) 成立,则有: 0