
§1.4概率的公理化定义及概率的性质 一个随机试验,如果他的数学模型时古典概型,那 么描述这个试验的样本空间、事件域和概率P 已在§3种得到了解决.在古典范围内试验的结果是 有限的。当试验结果为无限时,会出现一些本质性 困难,使问题不能像有限时那么容易解决。这里讨 论具有一某种“等可能性”的一类问题。 如果我们在一个面积为S,的区域中,等可能 的取值(图1.6)设区域①中任意一区域A,如果它
§1.4 概率的公理化定义及概率的性质 gjzsj
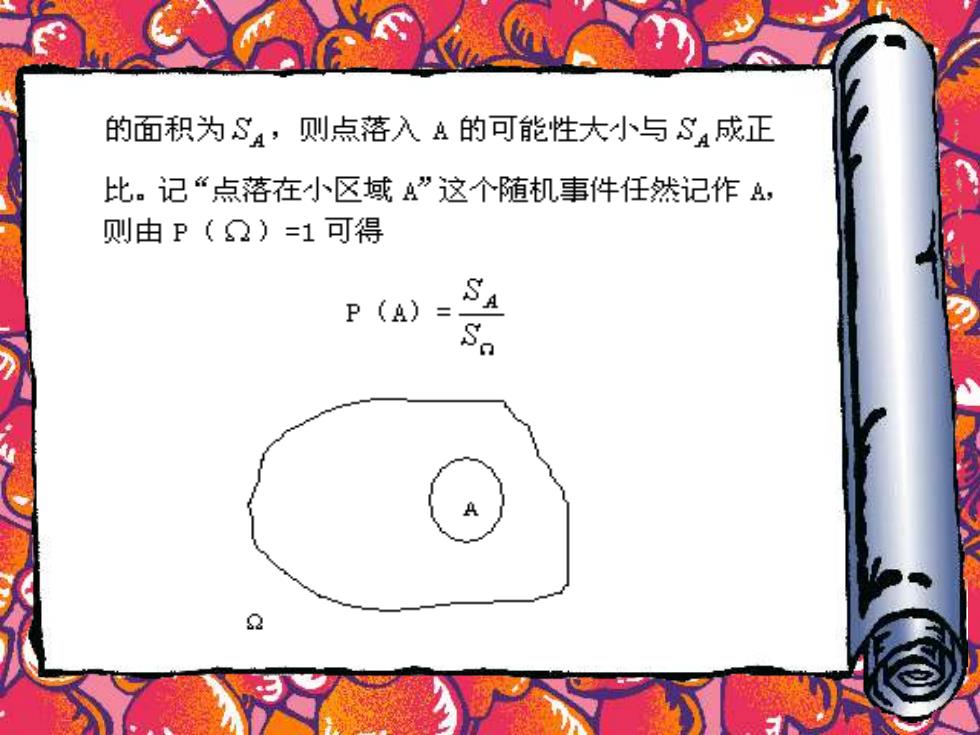
的面积为S4,则点落入A的可能性大小与S:成正 此。记“点落在小区域A”这个随机事件任然记作A, 则由P()=1可得 P(A)= S Sa A
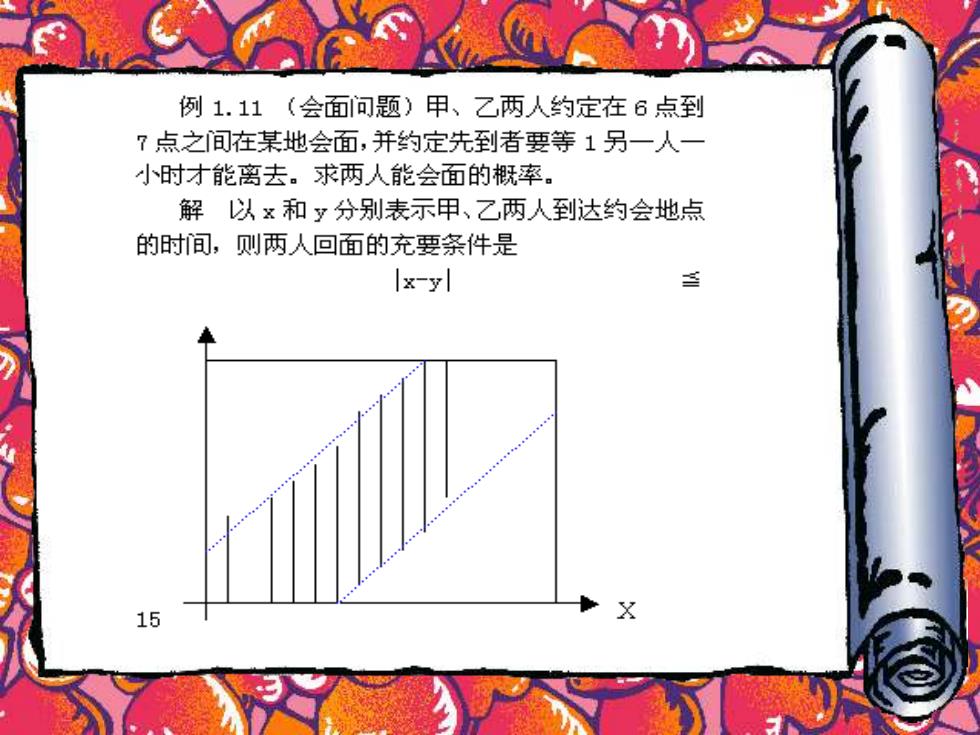
例1.11(会面问题)甲、乙两人约定在6点到 ?点之间在某地会面,并约定先到者要等1另一人一 小时才能离去。求两人能会面的慨率。 解以x和y分别表示甲、乙两人到达约会地点 的时间,则两人回面的充要条件是 -yl 15 X

在平面上建立直角坐标系图1.7。则(x,y)的 所有可能结果是边长60的正方形,而会面可能时间 是图中的阴影部分。 由等可能性质知: P(A)= S4.602-4527 Sa 602 16 例1.12浦丰投针问题。平面上画有等距离的 平行线,平行线间的距离为a(a>0),在平面任意投 掷一枚长1(1<a)的针,试求针与平行线相交的慨 率

解以x表示针的中点与最近的一条平行线的 距离,又以®表示针与此直线间的交角,知 以 0≤x≤ 2 0爸0英江 由这两式可以确定x平面上的一个矩形, 这时为了针与平行线相交,其充分条件是: x≤二sin& 2 由这个不等式表示的区域A是图中的阴影部分。 由等可能性知