
§6.2 三大统计分布 一、化平方分司 二、你南 三、F-你南 上页 页 返回

主主主王王王王王王 §6.2三大统计分布 本节介绍数理统计中的三个著名分布, 它们在参数估计和假设检验等统计推断问 题中有广泛应用. 一、X平方-分布 随机莎多一心格为一 分布N0,),则称x2=∑x=X好+x++x(6-8) 所服从的分布是自由度为的x-分布, 记为~x(m,称为x变量.为纪念英国著 名统计学家皮尔(K.Pearson,1857-1936) 上页 回
§6.2 三大统计分布 本节介绍数理统计中的三个著名分布, 它们在参数估计和假设检验等统计推断问 题中有广泛应用. 一、X平方-分布 定义6.1 设随机变量 独立且服从相同 分布 ,则称 (6-8) 所服从的分布是自由度为n的 -分布, 记为 ,称 为 -变量. 为纪念英国著 名统计学家皮尔(K.Pearson,1857-1936) X X Xn , , , 1 2 N(0,1) = = = + + + n i n Xi X X Xn 1 2 2 2 2 1 2 2 2 ~ ( ) 2 2 n n 2 n 2

牛布系为皮尔通分布,这是数理统计中 一个十分重要的概率分布. 士根据独立随机变量和的密度公式3-27)和数学 归纳法,可以证明:x()分布的概率密度函 数为(详见5])1一xe,x>0 f(x)=2T() 0 x≤0 (6-9) 其中(x是r-函数,定义见第四章附录2.图 6.1是x变量的概率密度函数(6-9)在几种不 工王王王王王 同参数下的图像
- 分布也称为皮尔逊 -分布. 这是数理统计中 一个十分重要的概率分布. 根据独立随机变量和的密度公式(3-27)和数学 归纳法,可以证明: -分布的概率密度函 数为(详见[5]) ,(6-9) 其中 是 -函数,定义见第四章附录2.图 6.1是 -变量的概率密度函数(6-9)在几种不 同参数下的图像. 2 2 ( ) 2 n = − − 0 , 0 , 0 2 Γ( ) 1 ( ) 2 2 2 1 2 x x e x f x n x n n n Γ(x) Γ 2
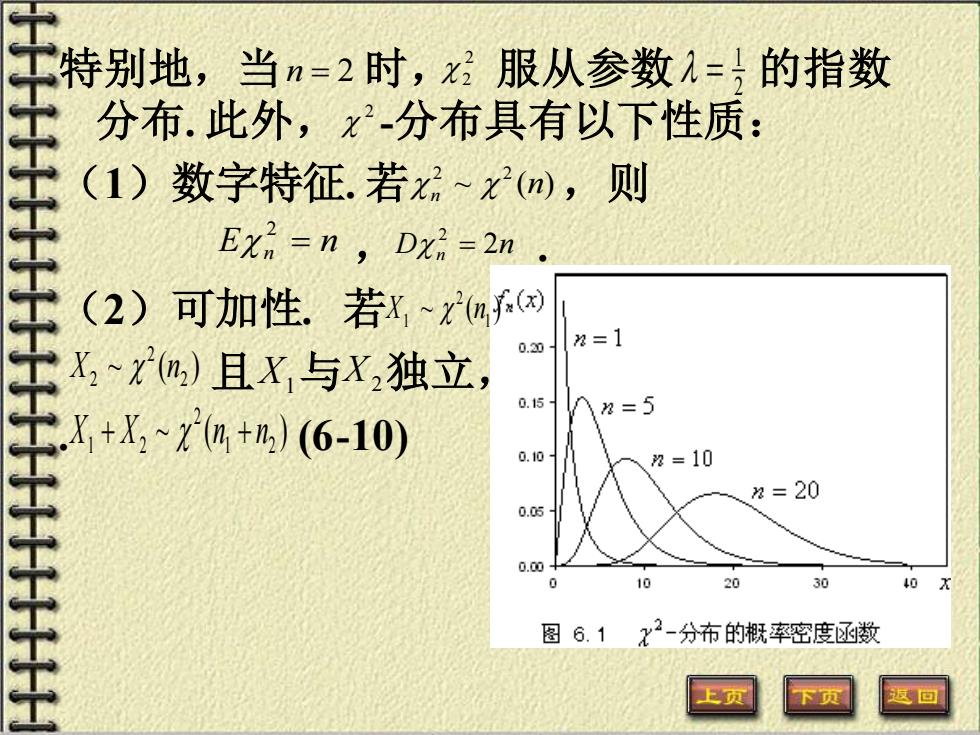
xP2(, 分布.此外,x-分布具有以下性质: (1)数字特征.若x~xm,则 Exn =n Dz:-2n (2)可加性.若x~闭 0.20 2=1 X2~)且X与X,独立, 0.15 八=5 X+X2ta+n)(6-10) 0.10 2=10 2=20 0.05 0.00 20 40 图6.1x2-分布的概率密度函数 回
特别地,当 时, 服从参数 的指数 分布. 此外, -分布具有以下性质: (1)数字特征. 若 ,则 , . (2)可加性. 若 且 与 独立,则 . (6-10) n = 2 2 2 2 1 = 2 ~ ( ) 2 2 n n E n = n 2 D n 2n 2 = ~ ( ) 1 2 1 X n ~ ( ) 2 2 2 X n X1 X2 ~ ( ) 1 2 2 1 2 X + X n + n
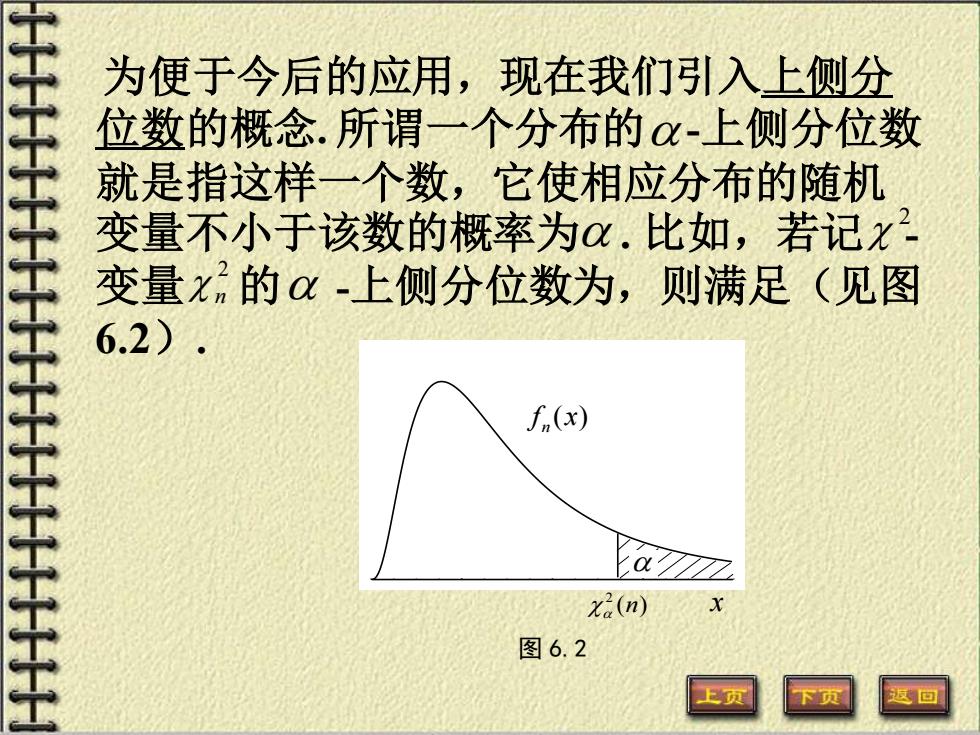
为便于今后的应用,现在我们引入上侧分 位数的概念.所谓一个分布的α-上侧分位数 就是指这样一个数,它使相应分布的随机 变量不小于该数的概率为.比如,若记x 变量x的-上侧分位数为,则满足(见图 6.2) f(x) x2(n) 图6.2
为便于今后的应用,现在我们引入上侧分 位数的概念. 所谓一个分布的 -上侧分位数 就是指这样一个数,它使相应分布的随机 变量不小于该数的概率为 . 比如,若记 - 变量 的 -上侧分位数为,则满足(见图 6.2). 2 2 n 图 6.2 ( ) 2 n f (x) n x