
材料力学教案第17讲教学方案弯曲变形(1)基本内中1.挠曲线。挠度与转角。2. 梁的刚度条件。容3.挠曲线的近似微分方程。4. 求弯曲变形的积分法
材 料 力 学 教 案 第 17 讲 教学方案 —— 弯曲变形(Ⅰ) 基 本 内 容 1. 挠曲线。挠度与转角。 2. 梁的刚度条件。 3. 挠曲线的近似微分方程。 4. 求弯曲变形的积分法

+七讲第教学1.梁的变形分析、挠曲线、挠度与转角的定义。目2:挠曲轴近似微分方程的建立的3.两次积分法求挠曲线方程、求指定截面的位移。4.求位移的例题分析。1.明确挠曲的连续、光滑的特点。重2.掌握在小变形情况下,挠度与转角之间的关系。点3.掌握利用小变形条件,推导出的挠曲线微分方程为近似难微分方程。点4.重点掌握在确定积分常数时,如何正确利用边界条件和连续条件。5.难点在于积分分段多时,积分常数的确定过于烦琐。本次教学计划学时:2学时。教课堂上应由工程中的弯曲实例引出问题,让学生了解在实际学安工程中,一方面要限制构件的变形,另一方面却利用构件的变形排来工作。讨论1.提出用哪些量去描述变形,这些量之间是否存在关系?2.求解变形通常用什么方法,怎样求?
第 十 七 讲 教 学 目 的 1. 梁的变形分析、挠曲线、挠度与转角的定义。 2. 挠曲轴近似微分方程的建立 3. 两次积分法求挠曲线方程、求指定截面的位移。 4. 求位移的例题分析。 重 点 、 难 点 1. 明确挠曲的连续、光滑的特点。 2.掌握在小变形情况下,挠度与转角之间的关系。 3.掌握利用小变形条件,推导出的挠曲线微分方程为近似 微分方程。 4. 重点掌握在确定积分常数时,如何正确利用边界条件和 连续条件。 5. 难点在于积分分段多时,积分常数的确定过于烦琐。 教 学 安 排 本次教学计划学时:2 学时。 课堂上应由工程中的弯曲实例引出问题,让学生了解在实际 工程中,一方面要限制构件的变形,另一方面却利用构件的变形 来工作。讨论 1.提出用哪些量去描述变形,这些量之间是否存在 关系?2.求解变形通常用什么方法,怎样求?

材料力学教案第六章 弯曲变形s6-1挠度与转角梁的刚度条件梁变形前后形状的变化称为变形,一般用各段梁曲率的变化表示。梁变形前后位置的变化称为位移,位移包括线位移和角位移,如图7-1所示。在小变形和忽略剪力影响的条件下,线位移是截面形心沿垂直于梁轴线方向的位移,称为规度,用√表示;角位移是横截面变形前后的夹角,称为转角,用0表示。而0(x)=dh(),,可见确定梁的位移,关键是确定规曲线方程v(x)。dx图7-1梁的位移梁的设计中,除了需要满足强度条件外,在很多情况下,还要将其弹性变形限制在一定范围内,即满足刚度条件[ ≤[>] [0] mx ≤[0] 式中的[]和[0]分别为梁的许用挑度和许用转角,可从有关设计手册中查得。$6-2挠度曲线的近似微分方程忽略剪力对变形的影响,梁平面弯曲的曲率公式为:式(a)表明梁轴线上任一点的曲率Y。p(x)与该点处横截M(xM(x)面上的弯矩M(α)成正比,而与该截面的抗弯刚度EI成反比。如图7-2所示。d而梁轴线上任一点的曲率与挠曲线方程v(x)之间存图 7-2 微段聚的变形在下列关系:
材 料 力 学 教 案 第六章 弯曲变形 §6-1 挠度与转角 梁的刚度条件 梁变形前后形状的变化称为变形,一般用各段梁曲率的变化表示。梁变形前后位置的变化称 为位移,位移包括线位移和角位移,如图 7-1 所示。在小变形和忽略剪力影响的条件下,线位移 是截面形心沿垂直于梁轴线方向的位移,称为挠度,用 v 表示;角位移是横截面变形前后的夹角, 称为转角,用 表示。而 dx dv x x ( ) ( ) = ,可见确定梁的位移,关键是确定挠曲线方程 v(x) 。 梁的设计中,除了需要满足强度条件外,在很多情况下,还要将其弹性变形限制在一定范围内, 即满足刚度条件 [ ] [ ] max max v v 式中的 [v] 和 [ ] 分别为梁的许用挠度和许用转角,可从 有关设计手册中查得。 §6-2 挠度曲线的近似微分方程 忽略剪力对变形的影响,梁平面弯曲的曲率公式为: 式(a)表明梁轴线上任一点的曲率 ( ) 1 x 与该点处横截 面上的弯矩 M (x) 成正比,而与该截面的抗弯刚度 EI 成 反比。如图 7-2 所示。 而梁轴线上任一点的曲率与挠曲线方程 v(x) 之间存 在下列关系:
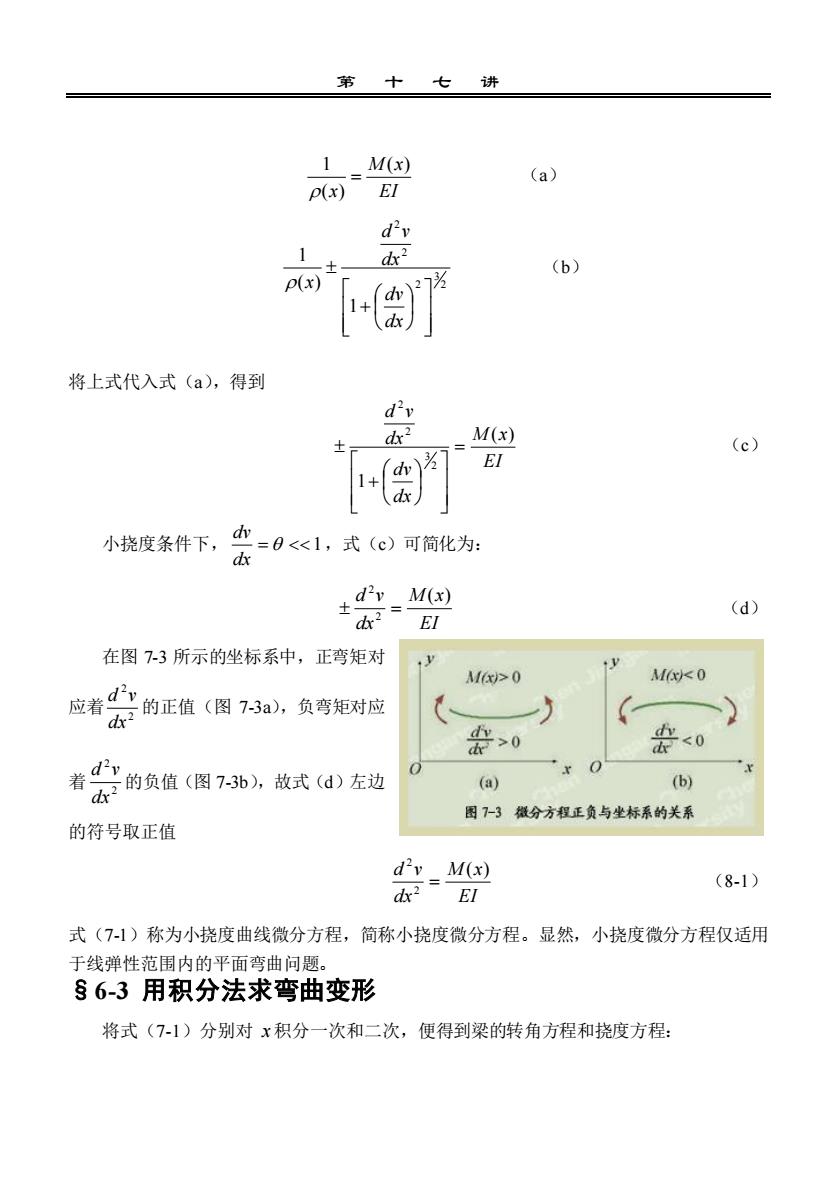
家++1M(x)(a)p(x)"ETdy1dx(b)()7p(x)(ax)将上式代入式(a),得到d'M(x)dx?(c)[1+()]EI(dxdy小挠度条件下,=0<<1,式(c)可简化为:dxd?y_ M(x)(d)dx?EI在图7-3所示的坐标系中,正弯矩对.3M(x)>0M(x<0应着d的正值(图7-3a),负弯矩对应产C2dx2>001-xC着尝的负值(图73b),故式(d)左边(b)(a)图7-3微分方程正负与坐标系的关系的符号取正值dv_ M(x)(8-1)dx?EI式(7-1)称为小挠度曲线微分方程,简称小挠度微分方程。显然,小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。s6-3用积分法求弯曲变形将式(7-1)分别对x积分一次和二次,便得到梁的转角方程和挠度方程:
第 十 七 讲 EI M x x ( ) ( ) 1 = (a) 2 3 2 2 2 1 ( ) 1 + dx dv dx d v x (b) 将上式代入式(a),得到 EI M x dx dv dx d v ( ) 1 2 3 2 2 = + (c) 小挠度条件下, = 1 dx dv ,式(c)可简化为: EI M x dx d v ( ) 2 2 = (d) 在图 7-3 所示的坐标系中,正弯矩对 应着 2 2 dx d v 的正值(图 7-3a),负弯矩对应 着 2 2 dx d v 的负值(图 7-3b),故式(d)左边 的符号取正值 EI M x dx d v ( ) 2 2 = (8-1) 式(7-1)称为小挠度曲线微分方程,简称小挠度微分方程。显然,小挠度微分方程仅适用 于线弹性范围内的平面弯曲问题。 §6-3 用积分法求弯曲变形 将式(7-1)分别对 x 积分一次和二次,便得到梁的转角方程和挠度方程:
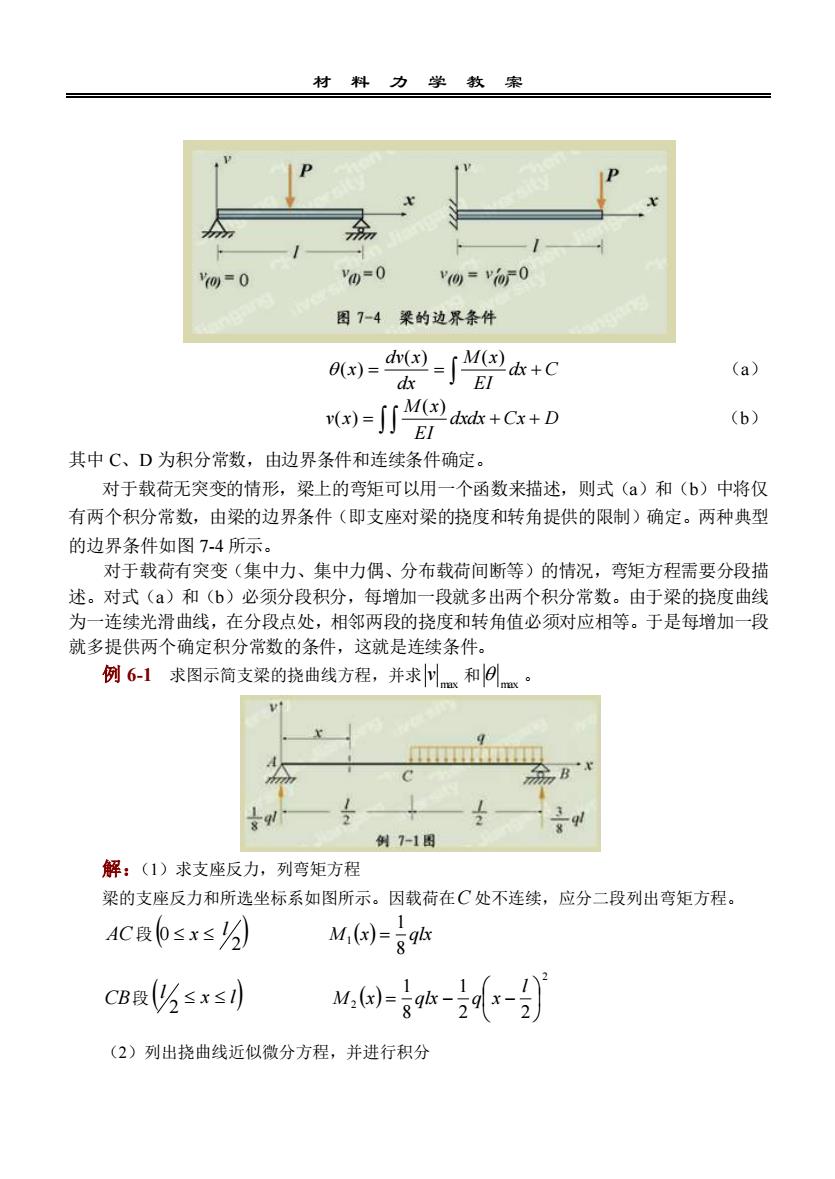
材料力学教索PPA10=0V(o)=V0-0(0=0图7-4梁的边界条件0()-- a+C(a)EIdx(a)= [[M()(b)dxdx + Cx + DEI其中C、D为积分常数,由边界条件和连续条件确定。对于载荷无突变的情形,梁上的弯矩可以用一个函数来描述,则式(a)和(b)中将仅有两个积分常数,由梁的边界条件(即支座对梁的挠度和转角提供的限制)确定。两种典型的边界条件如图7-4所示。对于载荷有突变(集中力、集中力偶、分布载荷间断等)的情况,弯矩方程需要分段描述。对式(a)和(b)必须分段积分,每增加一段就多出两个积分常数。由于梁的挠度曲线为一连续光滑曲线,在分段点处,相邻两段的挠度和转角值必须对应相等。于是每增加一段就多提供两个确定积分常数的条件,这就是连续条件。例6-1求图示简支梁的挠曲线方程,并求以和0mmuA+g例7-1图解:(1)求支座反力,列弯矩方程梁的支座反力和所选坐标系如图所示。因载荷在C处不连续,应分二段列出弯矩方程。AC段(0≤x≤)M,(x)= =qlxCB段(≤x≤1)M()--gx-9(x-2(2)列出挠曲线近似微分方程,并进行积分
材 料 力 学 教 案 = = dx + C EI M x dx dv x x ( ) ( ) ( ) (a) dxdx Cx D EI M x v x = + + ( ) ( ) (b) 其中 C、D 为积分常数,由边界条件和连续条件确定。 对于载荷无突变的情形,梁上的弯矩可以用一个函数来描述,则式(a)和(b)中将仅 有两个积分常数,由梁的边界条件(即支座对梁的挠度和转角提供的限制)确定。两种典型 的边界条件如图 7-4 所示。 对于载荷有突变(集中力、集中力偶、分布载荷间断等)的情况,弯矩方程需要分段描 述。对式(a)和(b)必须分段积分,每增加一段就多出两个积分常数。由于梁的挠度曲线 为一连续光滑曲线,在分段点处,相邻两段的挠度和转角值必须对应相等。于是每增加一段 就多提供两个确定积分常数的条件,这就是连续条件。 例 6-1 求图示简支梁的挠曲线方程,并求 max v 和 max 。 解:(1)求支座反力,列弯矩方程 梁的支座反力和所选坐标系如图所示。因载荷在 C 处不连续,应分二段列出弯矩方程。 AC 段 ( ) 2 0 l x M (x) qlx 8 1 1 = CB 段 ( x l) l 2 ( ) 2 2 2 2 1 8 1 = − − l M x qlx q x (2)列出挠曲线近似微分方程,并进行积分