
安培定律 例1求载流的有限长直导线外任一点的磁场。 [解1取直导线的中心为坐标原点,导线和z轴重合》 在圆柱坐标中计算。 B(r)=4o Idl'x R R=F-列 2 4πJcR3 (r,0,) 由对称性可知磁场与坐标无关 不失一般性,将场点取在0=0, a+za 场点坐标为(r,0,z) 源点坐标为(0,0,) z'=z-rtana dl 'a dz' dz'=rsec"a R=rseca dI'xR=ad-'x[ra,+(z-z)a.]=-djr2sec2a lexu@mail.xidian.edu.cn 11
安培定律 • 例1 求载流I的有限长直导线外任一点的磁场。 [解] 取直导线的中心为坐标原点,导线和z轴重合, 在圆柱坐标中计算。 由对称性可知磁场与坐标φ无关 不失一般性,将场点取在φ =0, 场点坐标为(r, 0, z) 源点坐标为(0,0,z′) lexu@mail.xidian.edu.cn 11 0 3 ' ( ) 4 C Idl R B r R µ π × = ∫ 2 ' tan ' sec sec z zr dz r R r α α α = − = = ˆ ˆ r z r ra za = + ' ' ˆz r za = Rrr = − ' ' ' ˆz dl a dz = 2 2 ' ' [ ( ') ] sec ˆ ˆ ˆ ˆ zr z dl R a dz ra z z a a r × = × + − =− φ α

安培定律 。由上可知: B=Lol in dT'xR 4πJ-12R3 z+1/2 sin a= ol-cosada 二0.4πr● V2+(e+112) z-1/2 sin a,=- a, (sina-sin4,) 22+(2-1/22 ·对于无限长直导线(→0),a1=π/2,2=-π/2,其产生的磁 场为 B=4出 lexu@mail.xidian.edu.cn 12
安培定律 • 由上可知: • 对于无限长直导线(l→∞),α1=π/2, α2 =-π/2,其产生的磁 场为 lexu@mail.xidian.edu.cn 12 2 1 /2 0 3 /2 0 0 1 2 ' 4 ˆ cos 4 ˆ (sin sin ) 4 l l I dl R B R I a d r I a r α φ α φ µ π µ α α π µ α α π − × = = − = − ∫ ∫ 2 2 2 2 2 1 ( / 2) / 2 sin ( / 2) / 2 sin z z l z l z z l z l + − − = + + + = α α 0 ˆ 2 I B a r φ µ π =

通量与散度 ·磁感应强度在有曲面上的通量简称为磁通量(或磁通),单位是 Wb(韦),用p表示。 Φ=∫B ·再看磁感应强度 B(r)=tJ(r)x 4πJr R "dv, 厅-F3 F-列 -%Jxv是r日r R 4πJPR V×(uQ)=Vu×0+V×0→Vu×0=V×(ug)-uV×0 c=会g2, R B(r)=VxJ(dv A(r) 4πJpR w→源处的积分 lexu@mail.xidian.edu.cn 13
通量与散度 • 磁感应强度在有曲面上的通量简称为磁通量(或磁通),单位是 Wb(韦),用φ表示。 • 再看磁感应强度 lexu@mail.xidian.edu.cn 13 s Φ= ⋅ B dS ∫ 0 3 ( ') ( ) ' 4 V Jr R B r dV R µ π × = ∫ r r r r r r − ′ = −∇ − ′ − ′ 1 3 0 0 1 1 ( ) ( ') ' ( ') ' 4 4 V V B r J r dV J r dV R R µ µ π π = − ×∇ = ∇ × ∫ ∫ ∇× =∇ × + ∇× ⇒∇ × =∇× − ∇× ( ) uQ u Q u Q u Q uQ u Q ( ) 0 ( ') ( ) ' 4 V J r B r dV R µ π = ∇× ∫ V∫ dv′ → 源处的积分 0 ( ') ( ) ' 4 V J r B r dV R µ π =∇× ∫ A r( )

通量与散度 B(r)=V×A→7.B(r)=0 -Note1:磁感应强度是管形场、无源(指散度源)场; -Note2:自然界不存在独立的磁荷; ·闭合曲面磁通量 Φ=B·d=0 S -Note1:通过任意闭合曲面S的磁通量为零 -Note2:磁力线闭合 ·磁通连续性原理 Φ=本Bd5=0 V.B(r)=0 S lexu@mail.xidian.edu.cn 14
通量与散度 – Note1:磁感应强度是管形场、无源(指散度源)场; – Note2:自然界不存在独立的磁荷; • 闭合曲面磁通量 – Note1:通过任意闭合曲面S的磁通量为零 – Note2:磁力线闭合 • 磁通连续性原理 lexu@mail.xidian.edu.cn 14 Br A ( ) =∇× ∇⋅ = B r() 0 0 S Φ= ⋅ = B dS ∫ ∇⋅ = B r() 0 0 S Φ= ⋅ = B dS ∫
环量与旋度 ·至此,我们己经研究了恒定磁场的通量及散度 恒定磁场的旋度及环量 考察无限长线电流的磁场沿其电流线上一 点为圆心垂直于导线平面内的圆周积分: ∮8di-i0-20-a ∮,B-al=4 lexu@mail.xidian.edu.cn 15
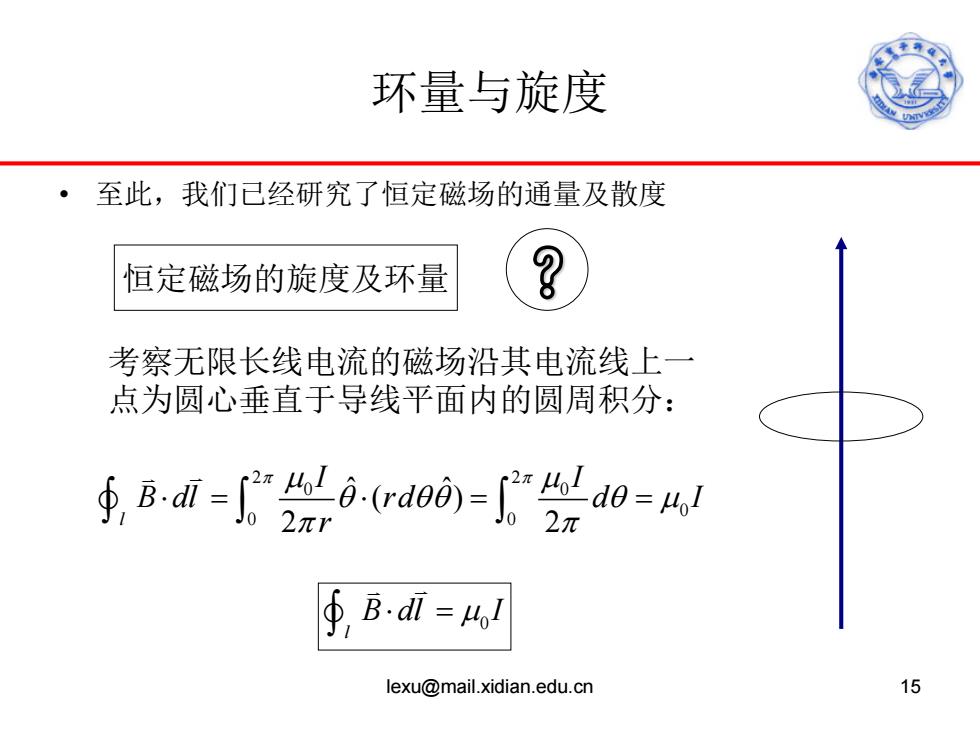
环量与旋度 • 至此,我们已经研究了恒定磁场的通量及散度 lexu@mail.xidian.edu.cn 15 恒定磁场的旋度及环量 ? 考察无限长线电流的磁场沿其电流线上一 点为圆心垂直于导线平面内的圆周积分: 2 2 0 0 0 0 0 ˆ ˆ ( ) l 2 2 I I B dl rd d I r π π µ µ θ θθ θ µ π π ⋅= ⋅ = = ∫∫ ∫ 0 l B dl I ⋅ = µ ∫