
1库仑定律和电场强度 例一圆环均匀分布总量Q的电荷,求其轴线上距圆心d 处的电场强度 p==dd.,=acos0d,+asin 1 2-acos'd,-asine'a,+d a-pad0 4元60 (a2+d2)月 ao a.= 2c,a2+ay4,(a2+dr月
1 库仑定律和电场强度 例 一圆环均匀分布总量Q的电荷,求其轴线上距圆心 d 处的电场强度 。 16
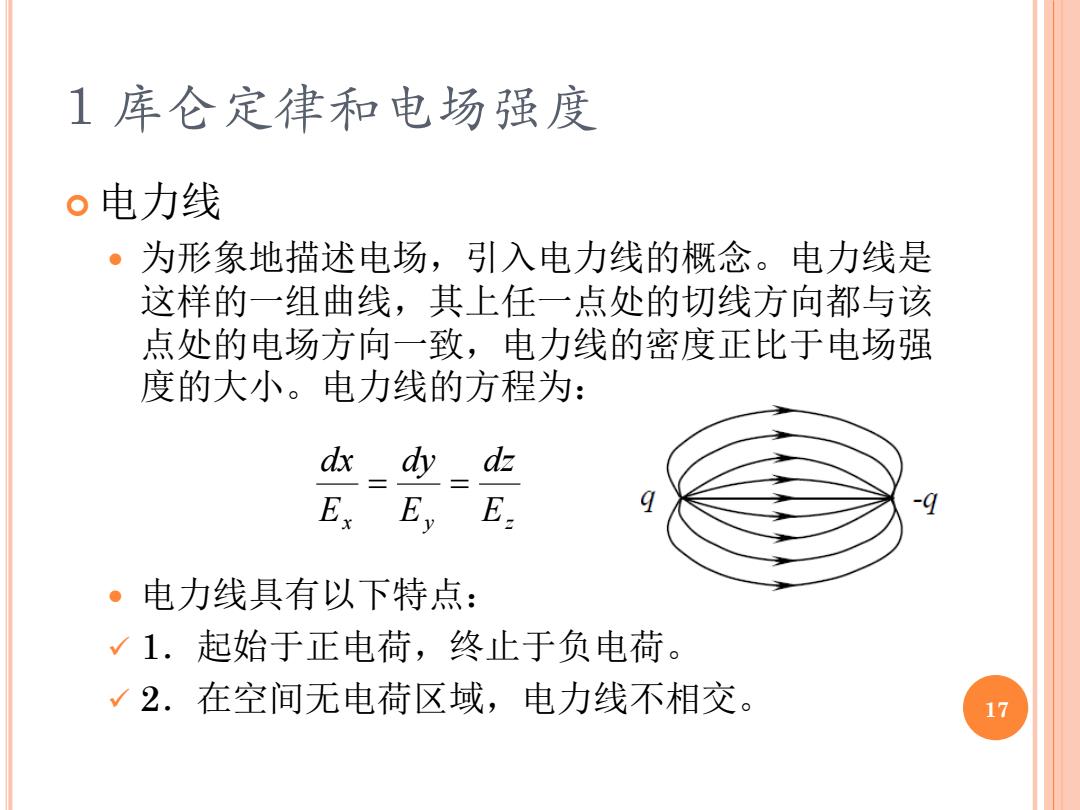
1库仑定律和电场强度 。电力线 ·为形象地描述电场,引入电力线的概念。电力线是 这样的一组曲线,其上任一点处的切线方向都与该 点处的电场方向一致,电力线的密度正比于电场强 度的大小。电力线的方程为: dx dy dz Ex Ey E q ·电力线具有以下特点: 1.起始于正电荷,终止于负电荷。 2.在空间无电荷区域,电力线不相交。 17
1 库仑定律和电场强度 电力线 为形象地描述电场,引入电力线的概念。电力线是 这样的一组曲线,其上任一点处的切线方向都与该 点处的电场方向一致,电力线的密度正比于电场强 度的大小。电力线的方程为: 电力线具有以下特点: ✓ 1.起始于正电荷,终止于负电荷。 ✓ 2.在空间无电荷区域,电力线不相交。 x y Ez dz E dy E dx = = 17
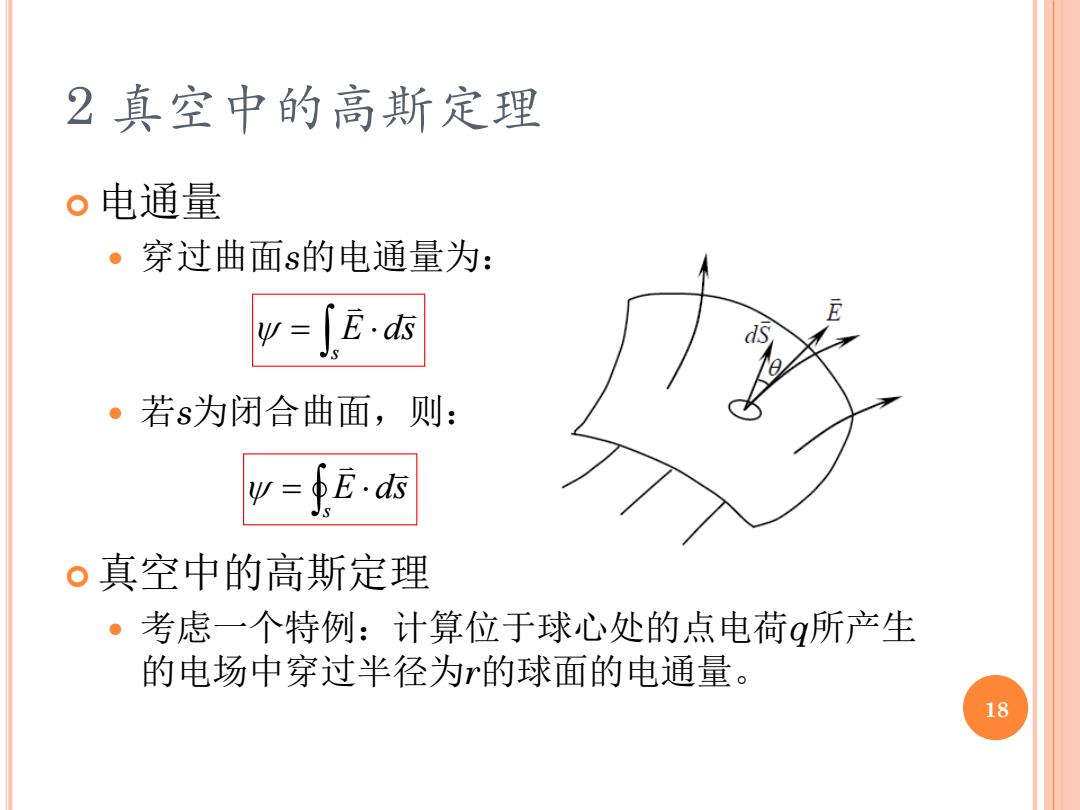
2真空中的高斯定理 。电通量 ·穿过曲面s的电通量为: w=∫E 。若s为闭合曲面,则: ds w=f 。真空中的高斯定理 考虑一个特例:计算位于球心处的点电荷g所产生 的电场中穿过半径为r的球面的电通量。 18
2 真空中的高斯定理 电通量 穿过曲面s的电通量为: 若s为闭合曲面,则: 真空中的高斯定理 考虑一个特例:计算位于球心处的点电荷q所产生 的电场中穿过半径为r的球面的电通量。 = s E ds = s E ds 18

2真空中的高斯定理 在球面上: E9 π6r尺 所以:v-本杰 这里下与d5方向一致。 9·4=9 4元80 80 该结果与球面半径无关,即穿出任一以g为球心的 球面的电通量均为q/,,在无电荷的区域,电力线 19 数目既不会增加,也不会减少
2 真空中的高斯定理 在球面上: 所以: 这里 与 方向一致。 ∴ 该结果与球面半径r无关,即穿出任一以q为球心的 球面的电通量均为 ,在无电荷的区域,电力线 数目既不会增加,也不会减少。 3 0 4 r q r E = = = s s ds r q r E ds 3 0 4 ds r = = = 2 0 0 2 2 0 2 0 2 0 sin 1 4 1 4 4 r d d r q ds r q r q ds s s 0 0 4 4 q q = = 0 q 19

2真空中的高斯定理 。再看两种较一般的情况: (1)穿过s和s,的电力线数目都是9,而穿过 S2 S s和s,的电力线必穿过s。 S 穿过s的电通量必为9。 (2).'穿出s和s,的电力线数目相等,故穿入 S2 s的电力线没有增多也没有减少地穿出s。 总的效应是∮E5=0 S q
2 真空中的高斯定理 再看两种较一般的情况: 20