
银川大学教学课件 物理学电子课件 功和能、机械能与机械能守恒定律 1、功和能、动能定理 2、保守力与非保守力势能 3、功能原理机械能守恒定律
1、 功和能、动能定理 2、 保守力与非保守力 势能 3、 功能原理 机械能守恒定律 物理学电子课件 银川大学教学课件 功和能、机械能与机械能守恒定律

复习 牛顿运动三定律 几种常见的力 万有引力、弹性力、摩擦力 牛顿运动定律的应用
复 习 牛顿运动三定律 几种常见的力 万有引力、弹性力、摩擦力 牛顿运动定律的应用

第二节功和能 一、功 1.直线运动中恒力的功 力对质点所作的功等于该力在位移方向 上的分量与位移大小的乘积 A=Fs cosa A=FAcosa=F.AF 说明 功是标量,没有方向,只有大小,但有正负,<元2,功A 为正值,力对物体作正功;0=π/2,功A=0,力对物体不作 功;>π2,功A为负值,力对物体作负功,或物体克服该 力作功。 单位:焦耳J1J=1Nm
第二节 功和能 一、功 1. 直线运动中恒力的功 力对质点所作的功等于该力在位移方向 上的分量与位移大小的乘积 说明 •功是标量,没有方向,只有大小,但有正负,q<p/2,功A 为正值,力对物体作正功;q=p /2,功A=0,力对物体不作 功;q>p /2,功A为负值,力对物体作负功,或物体克服该 力作功。 •单位:焦耳(J) 1J=1N·m m m F F q r A Fs = cos A F r F r = = cos
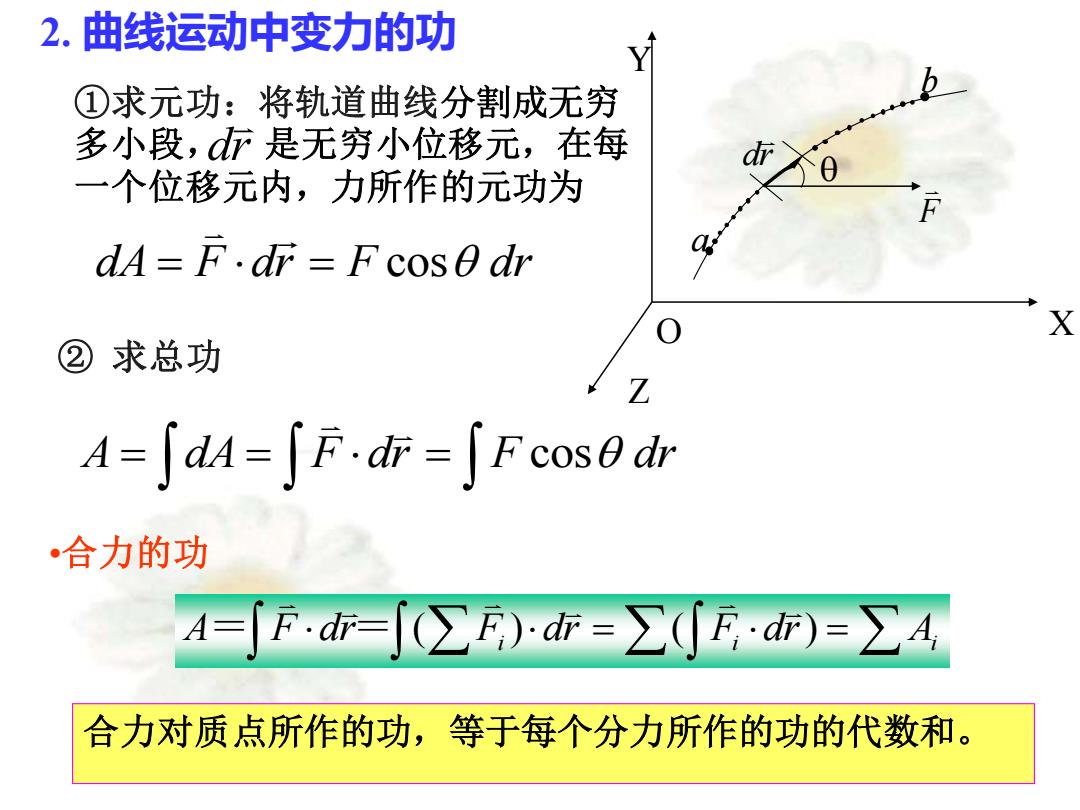
2.曲线运动中变力的功 ①求元功:将轨道曲线分割成无穷 多小段,厅是无穷小位移元,在每 一个位移元内,力所作的元功为 dA=F.dr =F cos0 dr X ② 求总功 A=∫dM=∫F,i=∫Fcos6dr 合力的功 A=∫F·=∫c∑F)=∑(F)=∑A 合力对质点所作的功,等于每个分力所作的功的代数和
dA = F dr = F cosq dr A = dA = F dr = F cosq dr •合力的功 i = i = Ai A F dr ( F ) dr ( F dr) = = 合力对质点所作的功,等于每个分力所作的功的代数和。 O X Z Y b a q dr F 2. 曲线运动中变力的功 ①求元功:将轨道曲线分割成无穷 多小段, 是无穷小位移元,在每 一个位移元内,力所作的元功为 dr ② 求总功

例某物体在平面上沿Ox轴的正方向前进。平 面上各处的摩擦系数不等,因而作用于物体的摩擦力 是变力。已知某段路面摩擦力的大小随坐标变化的规 律为: f=1+x(x≥0) 求从x=0到x=L,摩擦力所作的功
例 某物体在平面上沿 Ox 轴的正方向前进。平 面上各处的摩擦系数不等,因而作用于物体的摩擦力 是变力。已知某段路面摩擦力的大小随坐标变化的规 律为: 求从 ,摩擦力所作的功。 f = 1+ x ( 0) x x = 0到x = L