
1库仑定律和电场强度 。迭加原理 当真空中存在两个以上的点电荷时,实验表明,任 何两个点电荷间的作用力不受其它点电荷的影响, 所以点电荷g所受的力是其它所有点电荷对它的作 用力的矢量和,即满足迭加性。 F,())=F+F2++则=2 9〉二 下-列 其中F①表示处的点电荷9:对q的作用力。 6
1 库仑定律和电场强度 迭加原理 当真空中存在两个以上的点电荷时,实验表明,任 何两个点电荷间的作用力不受其它点电荷的影响, 所以点电荷q所受的力是其它所有点电荷对它的作 用力的矢量和,即满足迭加性。 其中 表示 处的点电荷 对q的作用力。 = − − = + + + = n i i n i i q q q q r r q q r r F r F F F 0 1 (1) (2) ( ) ( ) 4 ( ) (i) Fq ir i q 6

1库仑定律和电场强度 例有三个点电荷电量分别为9,=92=106C,4=-102C, 它们处于一个边长为1m的等边三角形的顶点上,求9所 受的力。 解:由图知下= 2 -a,=-a, 93 92 下-月= F-引=1 f-g=空a-4F-到-l 7
例 有三个点电荷电量分别为 C, C, 它们处于一个边长为1m的等边三角形的顶点上,求 所 受的力。 1 库仑定律和电场强度 6 1 2 10− q = q = 12 3 10− q = − q3 7

1库仑定律和电场强度 由叠加原理得: 93 9,G-9,厅-) 46F-F- 9j小会] =-9√5×10°a,(牛顿) 8
1 库仑定律和电场强度 由叠加原理得: 8
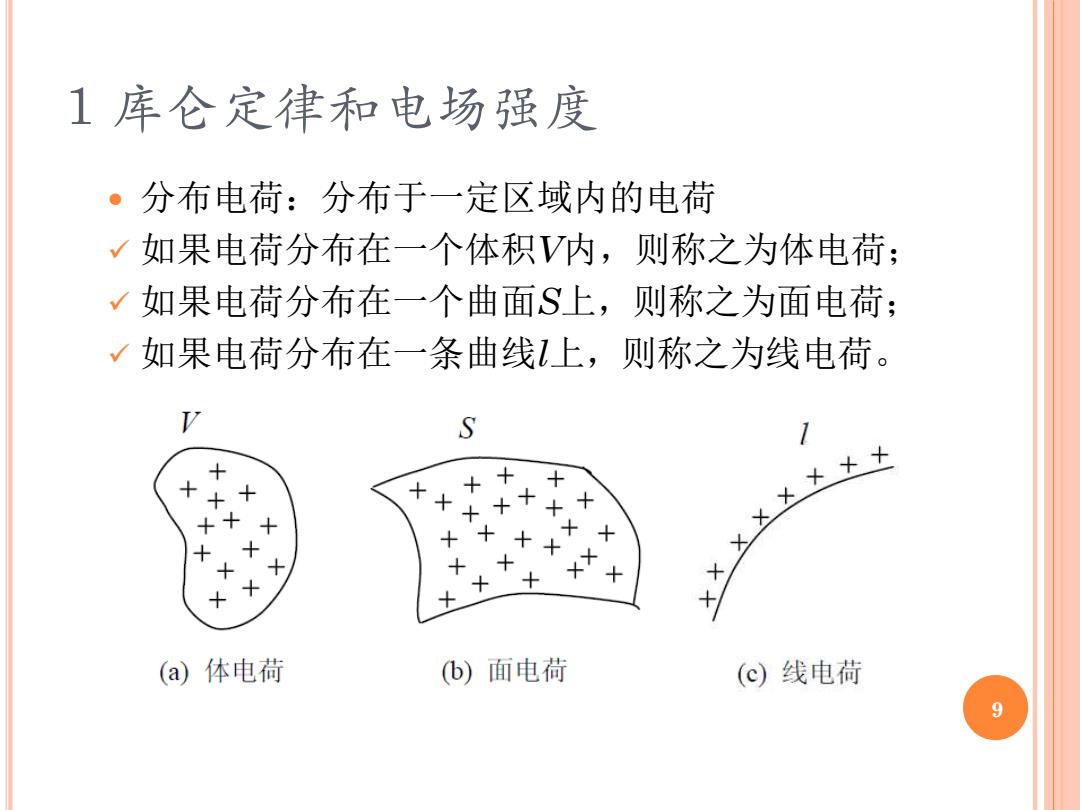
1库仑定律和电场强度 。分布电荷:分布于一定区域内的电荷 V 如果电荷分布在一个体积V内,则称之为体电荷: V1 如果电荷分布在一个曲面S上,则称之为面电荷: √如果电荷分布在一条曲线上,则称之为线电荷。 S + × + ×× + + + + 大大×××火+土 (a)体电荷 (b)面电荷 (c)线电荷 9
1 库仑定律和电场强度 分布电荷:分布于一定区域内的电荷 ✓ 如果电荷分布在一个体积V内,则称之为体电荷; ✓ 如果电荷分布在一个曲面S上,则称之为面电荷; ✓ 如果电荷分布在一条曲线l上,则称之为线电荷。 9

1库仑定律和电场强度 为了定量地描述电荷在区域内分布的疏密程度,引入 电荷密度的概念。 ·对于体电荷,在电荷分布在区域V内下处取体积元△V,, 若其中电荷的电量为△q,则定义: 体电荷密度:p(r)=lim △g=dg A-→0△VdW (C/m3)) ·类似地,可定义面电荷密度和线电荷密度分别为: p,(F)=lim △5→0 △s d函 (C/m2) p,()lim △9= dq (C/m〉 △1-→0 dl 10
1 库仑定律和电场强度 为了定量地描述电荷在区域内分布的疏密程度,引入 电荷密度的概念。 对于体电荷,在电荷分布在区域V内 处取体积元 , 若其中电荷的电量为 ,则定义: 类似地,可定义面电荷密度和线电荷密度分别为: (C/m²) (C/m) r V q dV dq V q r V = = →0 ( ) lim ( ) ds dq s q r s s = = →0 lim ( ) dl dq l q r l l = = →0 lim 体电荷密度: (C/m³) 10