
非线性物理:混沌物理 还要解决微分运算问题。通常采用由运算放大器组成的有源积分 电路来完成。一个常见的有源积分电路,其输入电压山,与输出电 压u。之间存在关系: uo = du. RC dt u =-RC dt ·非线性函数在电路上可以用二极管电路或二极管-运算放大 电路来实现。几种电路如下图所示:
非线性物理:混沌物理 • 还要解决微分运算问题。通常采用由运算放大器组成的有源积分 电路来完成。一个常见的有源积分电路,其输入电压 ui 与输出电 压 uo之间存在关系: • 非线性函数 f(x) 在电路上可以用二极管电路或二极管–运算放大 电路来实现。几种电路如下图所示: u dt RC u i 1 0 dui dt RC duo 1 dt du ui RC o
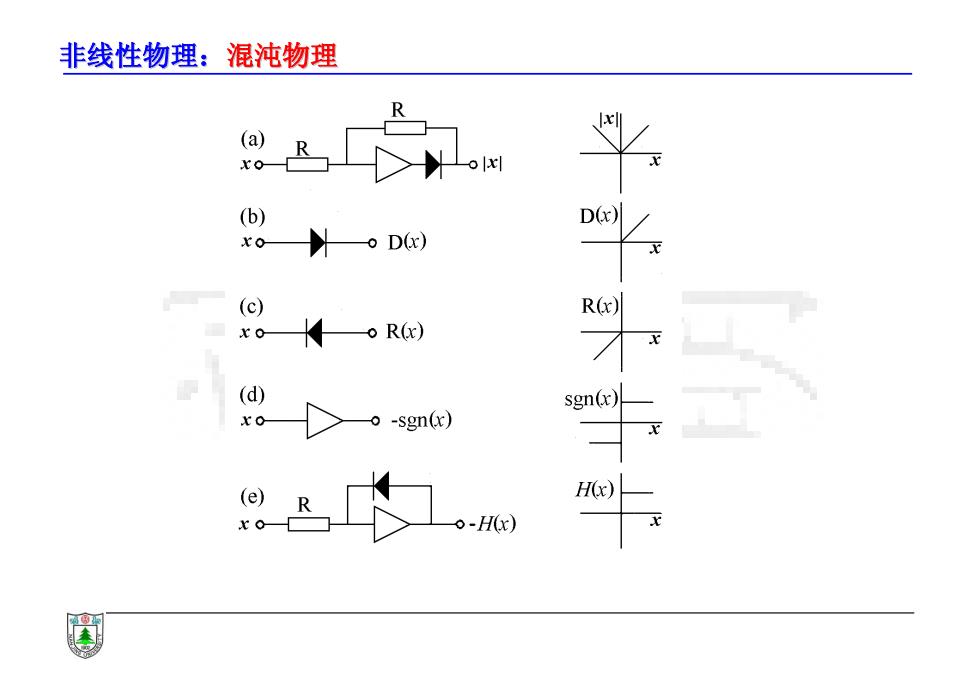
非线性物理:混沌物理 (a) ro (b) D(x) xo- oD(x) (c) R() -oR(x) (d) sgn(x) -sgn(x) (e H(x) -H(x)
非线性物理:混沌物理
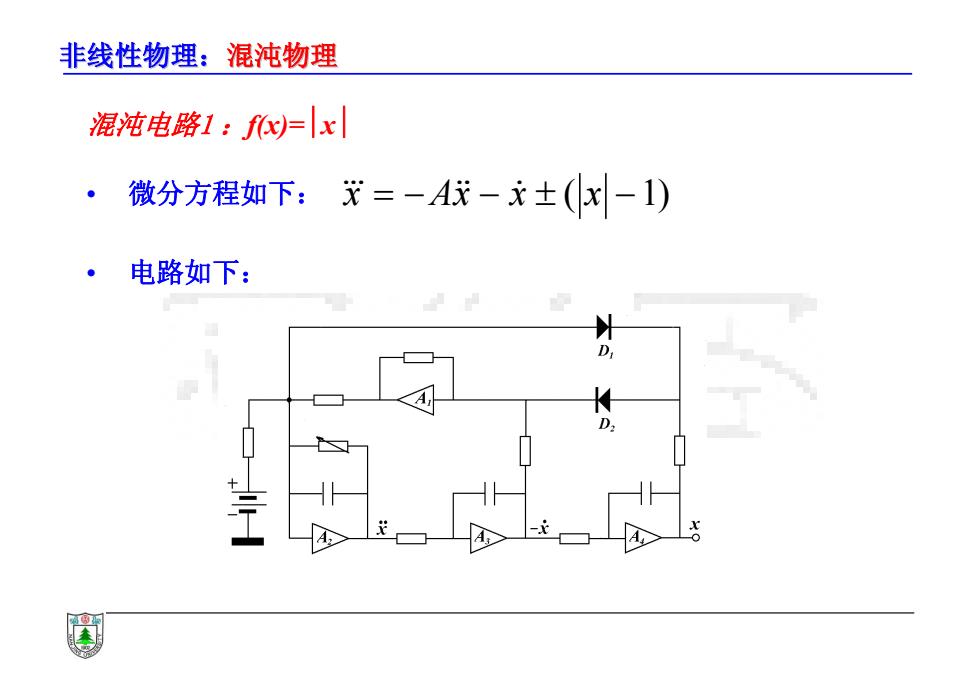
非线性物理:混沌物理 混沌电路1:fx)=|x 微分方程如下:x=-A代-元±(x-1) 电路如下: D
非线性物理:混沌物理 混沌电路1 :f(x)=x • 微分方程如下: • 电路如下: x Ax x ( x 1)

非线性物理:混沌物理 ·取方程右边的正负号为负号,初始条件为0,得0.5<A<0.8区间的 分岔图。当A由0.8向0.64085逼近时,系统以倍周期分岔进入混 沌。值小于0.64085后,出现类似于平方映射那样的带有大大小 小窗口的典型的混沌带。 .8 .5
非线性物理:混沌物理 • 取方程右边的正负号为负号,初始条件为0,得0.5<A<0.8区间的 分岔图。当A由0.8向0.64085逼近时,系统以倍周期分岔进入混 沌。A值小于0.64085后,出现类似于平方映射那样的带有大大小 小窗口的典型的混沌带

非线性物理:混沌物理 跃变非线性函数混沌: 利用运算放大器的内在非线性特性,即开环特性。当输入电压过 零时理想放大器的输出将从负饱和值跃变到正饱和值。 一个简单的以跃变非线性函数的微分方程为: 1, x>0 =-0.5 [x-sgn(x)] sgn(x)=0, x=0 -1, x<0 不同正负号对应的奇怪吸引子的形式很不相同。取正号时电路如 下图,电阻的选取是使运算放大器正向饱和电流为1mA,图中的 其它电阻均1k2
非线性物理:混沌物理 跃变非线性函数混沌: • 利用运算放大器的内在非线性特性,即开环特性。当输入电压过 零时理想放大器的输出将从负饱和值跃变到正饱和值。 • 一个简单的以跃变非线性函数的微分方程为: • 不同正负号对应的奇怪吸引子的形式很不相同。取正号时电路如 下图,电阻R的选取是使运算放大器正向饱和电流为1mA,图中的 其它电阻均1k。 x 0.5x x [x sgn(x)] 1, 0 0, 0 1, 0 sgn( ) xxx x