
非线性物理:混沌物理 。 电路方程如下: igiuc=cos( dt Cduc=in dt 些+c +uc uo cos(27fi+0) ·单结晶体管的V-关系g近似表示为: 4R2≈8()=a,+a,iL+ag2+a,记 可以监测电容两端电压uc(状态量)与可变参量uf之间的关系 来判断混沌进程
非线性物理:混沌物理 • 电路方程如下: L C L i dt du C R i gi u u ( ft+ dt di L cos 2 ) 1 L L C 0 cos 2 ) 2 1 C 0 2 u u ( ft+ dt du g C dt du R C dt d u L C C C • 单结晶体管的V-I关系 g 近似表示为: 3 3 L 2 R2 L 0 1 L 2 L u g(i ) a a i a gi a i • 可以监测电容两端电压 uC (状态量)与可变参量 u0、f 之间的关系 来判断混沌进程

非线性物理:混沌物理 实验取L=30mlH,C=0.07μf,R=1252,R=33.8k2,E。=28V,单结晶 体管BT33D。 取不同o可得系统不同运动状态:①当u,=0时,电路处于单 稳状态;②固定w,改变f使其逐步接近电路固有频率,电路出 现突变的锁频状态;③固定f)将山增加,在一定范围内出现倍 周期分岔与混沌。但不同f下出现倍周期分岔与混沌范围不同, 过程也不一样;④当f远离固有共振时,随山升高电路出现倍周 期分岔一混沌一反倍周期过程;⑤山值进一步升高,倍周期分岔 与混沌现象消失,电路表现出一般非线性电路所共有的畸变波形
非线性物理:混沌物理 • 实验取L=30mH, C=0.07F, R1=125, R3=33.8k, Ec=28V, 单结晶 体管BT33D。 • 取不同u0、f可得系统不同运动状态:① 当u0=0时,电路处于单 稳状态;② 固定u0,改变 f 使其逐步接近电路固有频率,电路出 现突变的锁频状态;③ 固定 f,将u0增加,在一定范围内出现倍 周期分岔与混沌。但不同 f 下出现倍周期分岔与混沌范围不同, 过程也不一样;④ 当 f 远离固有共振时,随u0升高电路出现倍周 期分岔-混沌-反倍周期过程;⑤ u0值进一步升高,倍周期分岔 与混沌现象消失,电路表现出一般非线性电路所共有的畸变波形

非线性物理:混沌物理 混沌特性的模拟电子电路: 能产生混沌行为的典型非线性常微分方程是由三个独立变量的一 阶微分方程组成。 可以将产生混沌行为的非线性微分方程写成一个三阶方程: x=ax+af()+ax+aaf (x)+asx+af(x)+a ·其中x)为非线性函数,由不同电子元件的伏安特性产生。 一个三阶方程描述的系统有三个李雅普诺夫指数,它是否具有混 沌行为要求其中至少有一个是正值,且散值之和非正。下表表示 一些对应的方程
非线性物理:混沌物理 混沌特性的模拟电子电路 : • 能产生混沌行为的典型非线性常微分方程是由三个独立变量的一 阶微分方程组成。 • 可以将产生混沌行为的非线性微分方程写成一个三阶方程: 1 2 3 4 5 6 7 x a x a f (x) a x a f (x) a x a f (x) a • 其中f(x)为非线性函数,由不同电子元件的伏安特性产生。 • 一个三阶方程描述的系统有三个李雅普诺夫指数,它是否具有混 沌行为要求其中至少有一个是正值,且散值之和非正。下表表示 一些对应的方程
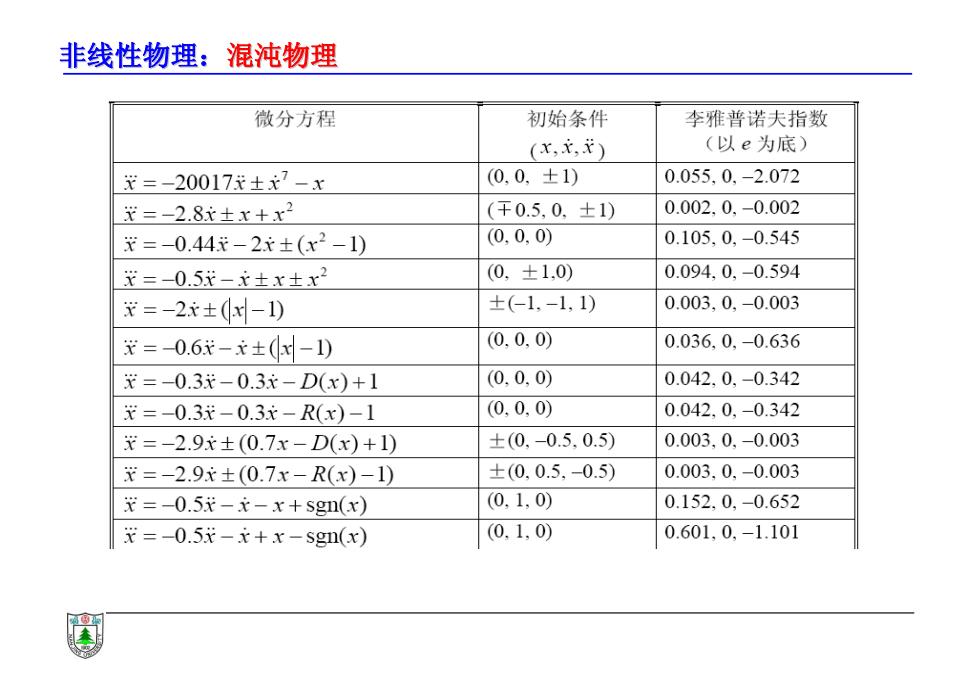
非线性物理:混沌物理 微分方程 初始条件 李雅普诺夫指数 (x,元,求) (以e为底) x=-20017:±x7-x 0,0.±1) 0.055,0.-2.072 ¥=-2.8x±x+x2 (千0.5,0.±1) 0.002.0.-0.002 =0.44t-2x±(x2-1) (0,0,0) 0.105,0,-0.545 x=-0.5-±x±x2 (0,±1,0) 0.094.0,-0.594 =-2±(-1) ±(-1.-1,1) 0.003,0,-0.003 ¥=-0.6x-x±-10 (0.0,0) 0.036,0,-0.636 =-0.3求-0.3x-D(x)+1 (0.0,0) 0.042,0,-0.342 ¥=0.3元-0.3x-R(x)-1 (0,0,0) 0.042,0,-0.342 x=-2.9x±(0.7x-D(x)+1) ±(0,0.5,0.5) 0.003,0.-0.003 x=-2.9x±(0.7x-R(x)-1) ±(0.0.5,-0.5) 0.003.0.-0.003 戈=0.5求--x+sgn(x) (0,1,0) 0.152.0,-0.652 =-0.5+x-sgn(x) (0.1,0) 0.601,0,-1.101
非线性物理:混沌物理

非线性物理:混沌物理 x=-0.7-元-x+H(x) (0.1.0) 0.085.0.-0.785 x=-0.4x-x-x+2S(x) (0.1,0) 0.072.0,-0.472 =-0.4r-x+x-2S(x) (0.1,0) 0.091,0,-0.491 =-0.19x+2tanh(x) (0.1,0) 0.128,0,-0.318 =-0.19+x-2tanh(x) (0.1,0) 0.067.0.-0.257 =-3.7x±(x-x3) (0.±0.5,0) 0.002.0.-0.002 ¥=-0.6求+2.8x-x3-x (0,1,0) 0.034,0,-0.634 ¥=0.7代-+x-x3 (0.1.0) 0.138.0,-0.838 =-0.35求--x+x3 (0.1.0) 0.082.0,-0.432 x=-0.2x-x±sin(x) (0,1,0) 0.123.0,-0.323
非线性物理:混沌物理