
k(k-1)+2k-九。k(k+1)-元 Ck+2= (k+2(k+1) (k+2)(k+1) y(x)=(x)+(x): 可以证明y、Jy2(x)在x=±1时,级数发散.(证明从略) 对于本征值问题: -)岛y=。只能取定值时,级数才能收数 =有界 若孔=1(1+1)(1=0,1,2,.) ,-k飞+-+.-0-0+k+0 6+24+)6,= (k+2(k+1) 6
6 ( ) ( )( ) ( ) ( )( ) 2 1 2 1 2 1 2 1 k k k k k k k k c c c k k k k + − + − + − = = + + + + 2 2 1 1 2 2 2 1 0 0 , k k k k k k y c x y c x + + = = = = ( ) ( ) ( ) 1 2 y x y x y x = + . 可以证明y1 (x)、y2 (x)在x = 1时,级数发散. (证明从略) 对于本征值问题: ( ) 2 1 1 0 x d dy x y dx dx y = − + = = 有界 只能取一定值时,级数才能收敛. 若 = + = l l l ( 1 0,1,2, ) ( ) ( ) ( ) ( )( ) ( )( ) ( )( ) 2 1 1 1 2 1 2 1 k k k k k l l l k l k c c c k k k k + + − + − + + = = − + + + +

当k=I时, (1-k)(1+k+1) C+2=0,→C44=C46=.=0 Ck+2= (k+2)(k+1) I为偶数时,y)退化为次的多项式,y2c)在x=±1发散,故 应该排除y2x); 为奇数时,y2()退化为次的多项式,y4(X)在x=±1发散,故 应该排除y(). (1-k)(1+k+1) (k+2)(k+) (1-k+2(1+k-1) k(k-1) k(k-1) 1(1-1) k=l: 2(21-1) C1, k=1-2:9-4=- 0 4(21-3)
7 ( )( ) ( )( ) 2 1 2 1 k k l k l k c c k k + − + + = − + + 当 k l = 时, 2 4 6 0, 0 l l l c c c + + + = → = = = l为偶数时,y1 (x)退化为l次的多项式,y2 (x)在x = 1发散,故 应该排除y2 (x); l为奇数时,y2 (x)退化为l次的多项式,y1 (x)在x = 1发散,故 应该排除y1 (x). ( )( ) ( )( ) 2 1 . 2 1 k k l k l k c c k k + − + + = − + + ( )( ) ( ) 2 2 1 , 1 k k l k l k c c k k − − + + − = − − ( ) ( )( ) 2 1 , 2 1 k k k k c c l k l k − − = − − + + − k l = : ( ) ( ) 2 1 , 2 2 1 l l l l c c l − − = − − k l = − 2 : ( )( ) ( ) ( ) ( )( )( ) ( )( ) 4 2 2 3 1 2 3 2 , 4 2 3 2 4 2 1 2 3 l l l l l l l l l c c c l l l − − − − − − − = − = − − − −
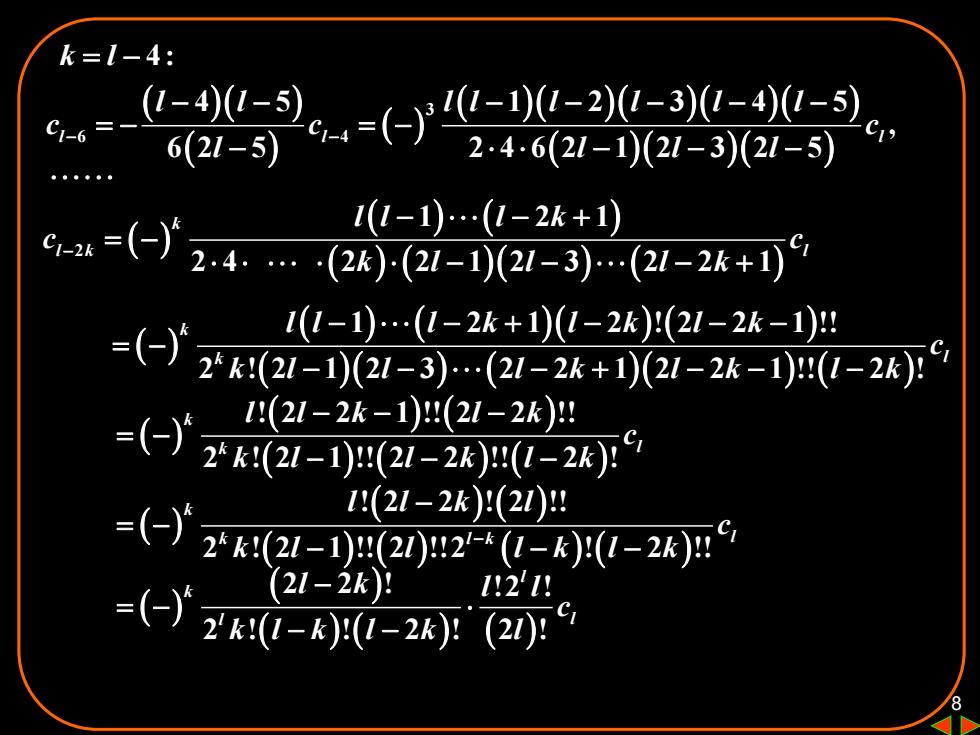
k=l-4: s=-《-。-yg=02-2000g 6(21-5) 246(21-1(21-3)(21-5) 1(1-).(1-2k+) c=(-24(2h)-(2-i021-3(21-2k+0 =(-) 11-).(1-2k+1(1-2k)(21-2k-1)H 2k(21-1)21-3)(21-2k+)2-2k-1)r(1-2k):7 I(21-2k-1)(21-2k)H 2*k(21-1)(21-2k)H(1-2k)1 =(-) I:(21-2k)(2I)H 2*k(21-1)H(2)2-*((I-k)(1-2k)H =( (21-2k)日 1214 2Yk(1-k)(1-2k): (2)1
8 k l = − 4 : ( )( ) ( ) ( ) ( )( )( )( )( ) ( )( )( ) 3 6 4 4 5 1 2 3 4 5 , 6 2 5 2 4 6 2 1 2 3 2 5 l l l l l l l l l l l c c c l l l l − − − − − − − − − = − = − − − − − ( ) ( ) ( ) ( ) ( )( ) ( ) 2 1 2 1 2 4 2 2 1 2 3 2 2 1 k l k l l l l k c c k l l l k − − − + = − − − − + ( ) ( ) ( )( ) ( ) ( )( ) ( )( ) ( ) 1 2 1 2 ! 2 2 1 !! 2 ! 2 1 2 3 2 2 1 2 2 1 !! 2 ! k k l l l l k l k l k c k l l l k l k l k − − + − − − = − − − − + − − − ( ) ( ) ( ) ( ) ( ) ( ) ! 2 2 1 !! 2 2 !! 2 ! 2 1 !! 2 2 !! 2 ! k k l l l k l k c k l l k l k − − − = − − − − ( ) ( ) ( ) ( ) ( ) ( ) ( ) ! 2 2 ! 2 !! 2 ! 2 1 !! 2 !!2 ! 2 !! k k l k l l l k l c k l l l k l k − − = − − − − ( ) ( ) ( ) ( ) ( ) 2 2 ! !2 ! 2 ! ! 2 ! 2 ! l k l l l k l l c k l k l k l − = − − −

= (21-2k)1 2'(2 2'k:(1-K)1-2K):(2I)月 (2) (21-2k) 2'(9 一c-)700- 内a爱瑞4-a内-名V22 1-2k 1+1 为奇数时,k=0,12,2, (+1)/2 (21-2k)月 ()=三F)2k-k)-2 (2I-2k)! 阶勒让德多项式 21
9 ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 ! 2 ! 2 ! ! 2 ! 2 ! l k l l l k l c k l k l k l − = − − − ( ) ( ) 2 2 ! 2 ! l l l c l 令 = ( ) ( ) ( ) ( ) 2 2 2 ! 2 ! ! 2 ! k l k l l k c k l k l k − − = − − − l为偶数时, ( ) ( ) ( ) ( ) ( ) / 2 2 1 0 2 2 ! 0,1,2, , , 2 2 ! ! 2 ! l k l k l k l l k k y x x k l k l k − = − = = − − − l为奇数时, ( ) ( ) ( ) ( ) ( ) ( 1 / 2 ) 2 2 0 2 2 ! 2 ! ! 2 ! l k l k l k l k y x x k l k l k + − = − = − − − 1 0,1,2, , , 2 l k + = ( ) ( ) ( ) ( ) ( ) 2 2 0 2 2 ! 2 ! ! 2 ! l k l k l l k l k P x x k l k l k − = − == − − − l阶勒让德多项式

问-222 (21-2k)1 2 (1=偶) r-2,N= 21 1+1 (1=奇) 综上: -]= 本征值问题. y儿=有界 =(1+1)(1=0,1,2,. 本征值. -a (21-2k月 本征函数 y(x)=cP(x)
10 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 0 2 2 ! 2 , 2 ! ! 2 ! 1 , 2 N k l k l l k l l l k P x x N k l k l k l l − = = − == − = − − + = , 偶 奇 综上: ( ) 2 1 1 0 x d dy x y dx dx y = − + = = 有界 = l l l ( + = 1 0,1,2, . ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 0 2 2 ! 2 ! ! 2 ! l k l k l l k l k P x x k l k l k − = − == − − − ( ) ( ) l y x cP x = —— 本征值问题. —— 本征值. —— 本征函数