
例8-3:正弦交流电路中()=100cos(01-平)4%=2aad/s 试求l)t=0.5S时(2)ot=2.5nrad时(3)ot=受rad时, 电流的大小及实际方向。 ()1=05s,i=100c0s(2×0.5-)=10c0s(-平)=-100cs7 =-50v2=-70.7mA b→a 2)o1=2.5rad,i=10co257-7)=10cos2r+罕)=100cos4 =50/2=70.7mA a-→b (3)ot=罗ad,i=100cos(Ξ-平)=100cos平=70.7n4 a->b
例8-3:正弦交流电路中, , 试求: i t t ) mA 4 ( ) 100 cos( p w w 2p rad /s 电流的大小及实际方向。 (1) t 0.5 S 时(2)w t 2.5p rad 时 时, 2 (3) t rad p w 4 ) 100 cos 4 ) 100 cos( 4 (1) 0.5 100 cos(2 0.5 p p p p t s,i p 50 2 70.7mA b a 4 ) 100 cos 4 ) 100 cos(2 4 2 2.5 , 100 cos(2.5 p p p p ( )w t p rad i p 50 2 70.7mA a b 解: t rad i 70.7mA 4 ) 100 cos 2 4 , 100 cos( 2 (3) p p p p w a b
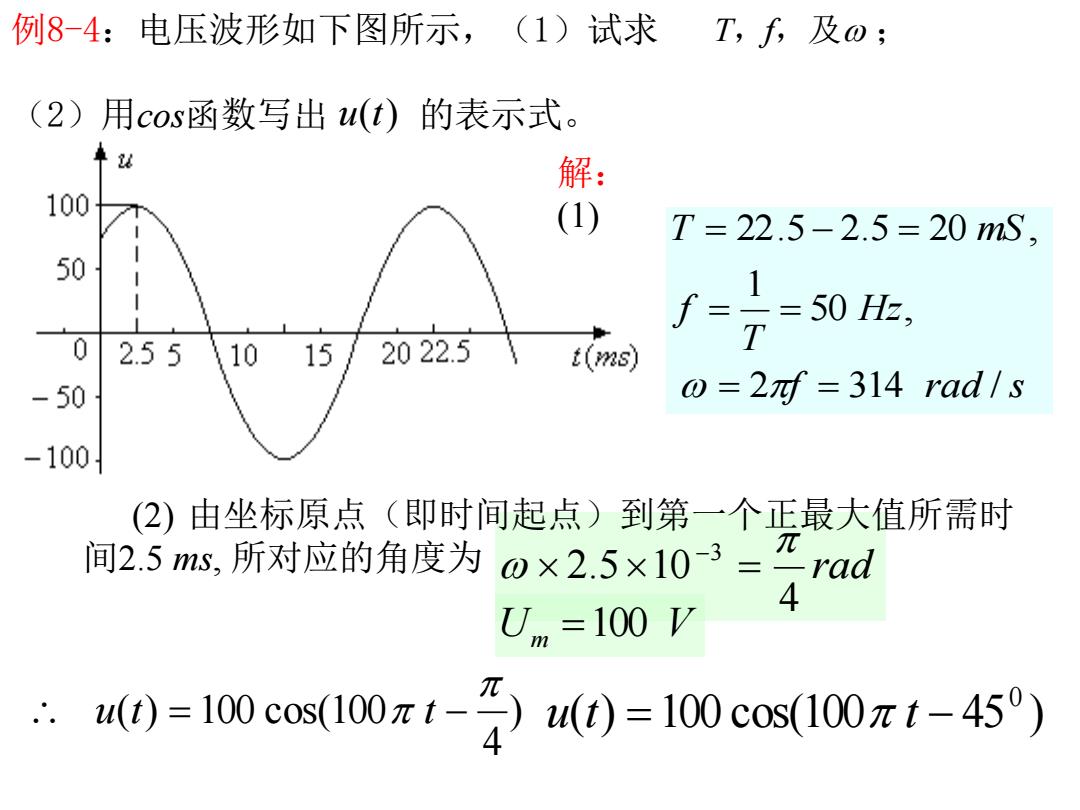
例8-4:电压波形如下图所示,(1)试求 T,f及0; (2)用cos函数写出u(t)的表示式。 解: 100 (1) T=22.5-2.5=20mS, 50 1 f==50Hz, 0 2.55101572022.5 t(s) T -50 o=2nf=314 rad/s -100 (2)由坐标原点(即时间起点)到第一个正最大值所需时 间2.5ms,所对应的角度为0×2.5×103-元rad π 4 U,=100 V 4)=100cos(100z1-至40=100cos100元1-450)
解: (1) 例8-4:电压波形如下图所示,(1)试求 T,f,及w ; (2)用cos函数写出 u(t) 的表示式。 f rad s Hz T f T mS 2 314 / 50 , 1 22.5 2.5 20 , w p rad 4 2.5 10 3 p w (2) 由坐标原点(即时间起点)到第一个正最大值所需时 间2.5 ms, 所对应的角度为 ) 4 ( ) 100 cos(100 p u t p t ( ) 100 cos(100 45 ) 0 u t p t Um 100 V
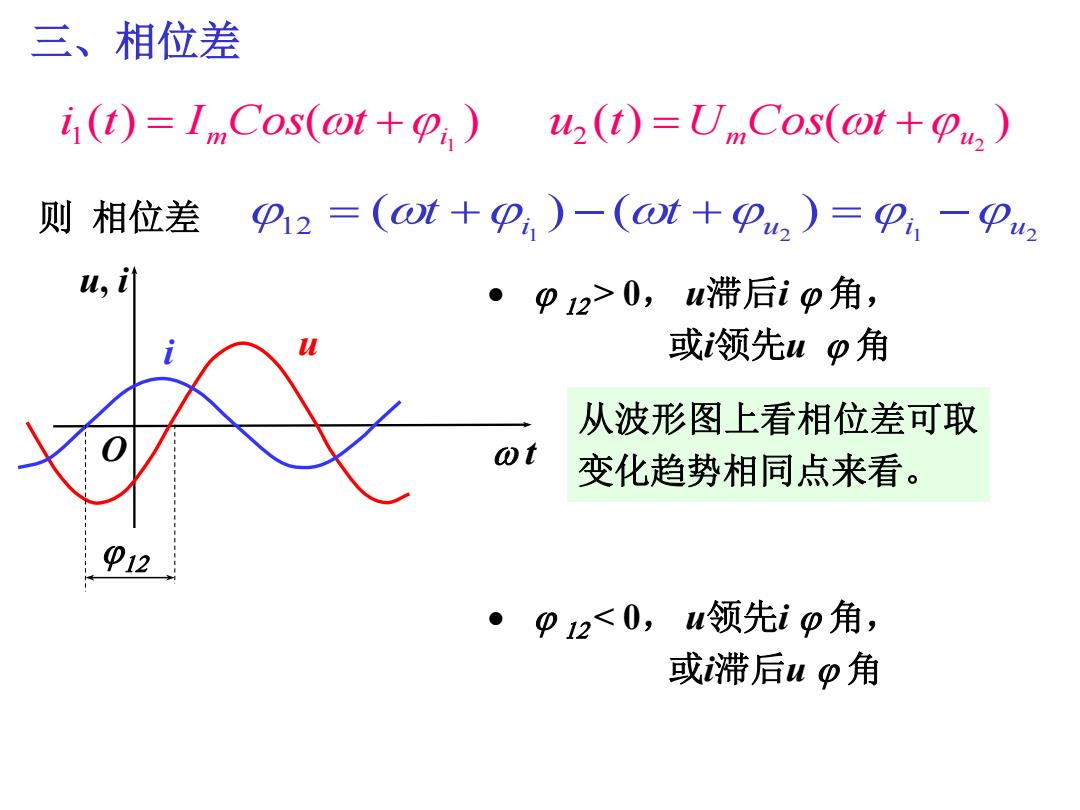
三、相位差 i(t)=I Cos(ot+i)u2 (t)=(ot+ 则相位差 p12=(ot+p)-(ot+Pu,)=P,-P2 ,计 。p2>0,u滞后ip角, 或领先wp角 从波形图上看相位差可取 变化趋势相同点来看。 12 ●p2<0,u领先ip角, 或滞后up角
三、相位差 则 相位差 ( ) ( ) ( ) ( ) 1 1 2 m u2 m i i t I Cos wt u t U Cos wt 1 2 1 2 ( ) ( ) 1 2 i u i u wt wt w t u, i i u 12 O 12> 0, u滞后i 角, 或i领先u 角 从波形图上看相位差可取 变化趋势相同点来看。 12< 0, u领先i 角, 或i滞后u 角
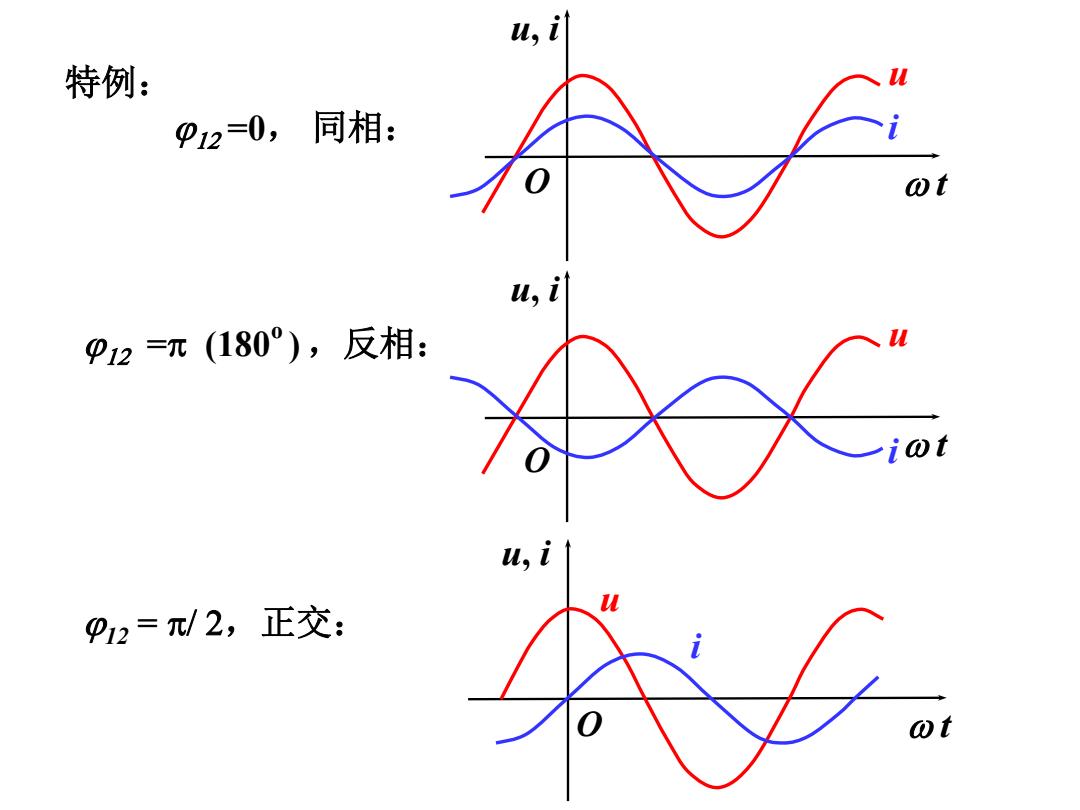
w,计 特例: p2=0,同相: ot P2=π(180°),反相: u,i P2=/2,正交: ot
12 =0, 同相: 12 =p (180o ),反相: 特例: w t u, i u i O w t u, i u O i 12 = p/ 2,正交: w t u, i u i O