
例如: B B=0 r IdI r 二.毕一萨定律的应用 1.载流直导线的磁场 求距离载流直导线为α处 一点P的磁感应强度 解 dB=toIdlsin 4π 8-a-经m0
例如: I l d P I l d I l r d B r B r B r B = 0 二.毕-萨定律的应用 1. 载流直导线的磁场 I a I l d r B 解 2 0 d sin 4 d r I l B = 求距离载流直导线为a处 一点P 的磁感应强度 B 2 0 d sin 4 d r I l B B = = P
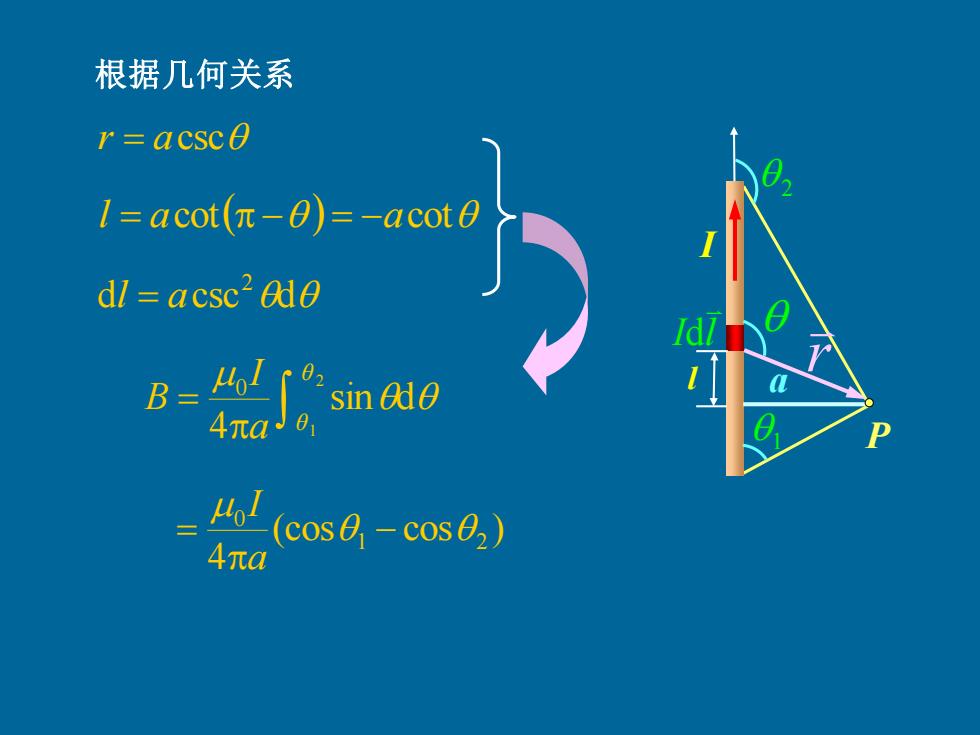
根据几何关系 r acsco 1=acot(π-O)=-acot0 dl acsc2 0d0 B= sin ado 4πaJ8 D 编csA-c风)》
1 2 r = acsc d csc d 2 l = a l = acot( − ) = −acot 根据几何关系 (cos cos ) 4 1 2 0 − = a I = 2 1 sin d 4 0 θ a θ I B I a I l d r P l
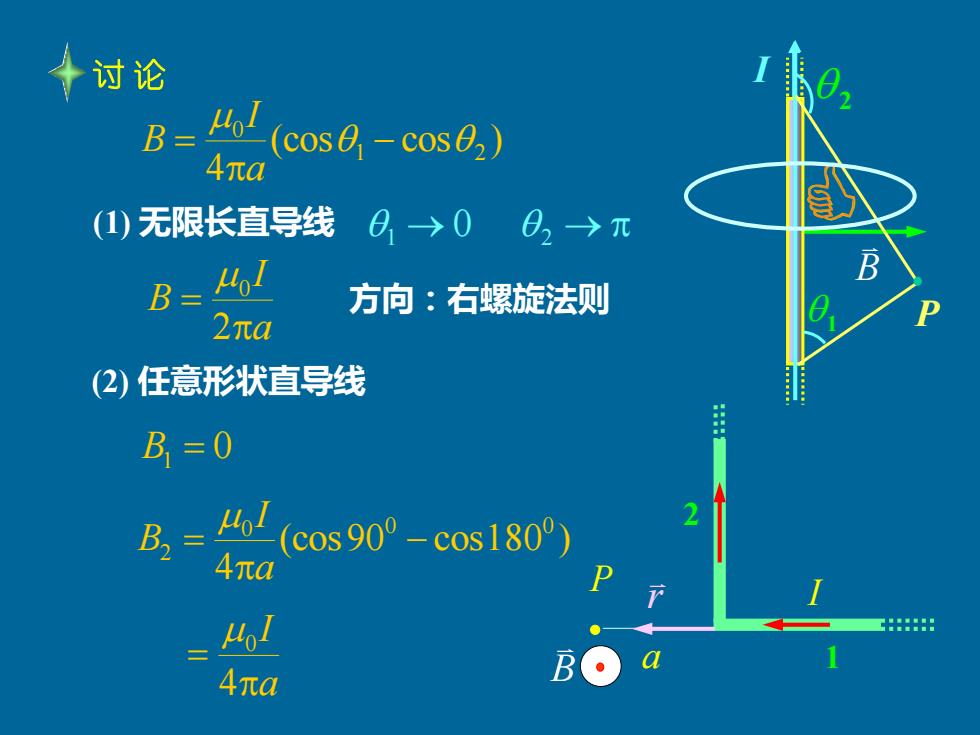
十讨论 B= (cos0-cos0,) 4πa (1)无限长直导线0,→0 02→元 B=46I 方向:右螺旋法则 2πa (2)任意形状直导线 B=0 B,=6/(cos90°-c0s180) 2 4元a 46 C::8 4πa B
(1) 无限长直导线 (cos cos ) 4 1 2 0 − = a I B 1 → 0 2 → a I B = 2 0 方向:右螺旋法则 B (2) 任意形状直导线 P a I 1 2 B1 = 0 (cos90 cos180 ) 4 0 0 0 2 − = a I B a I = 4 0 B r 讨 论 I 1 2 P
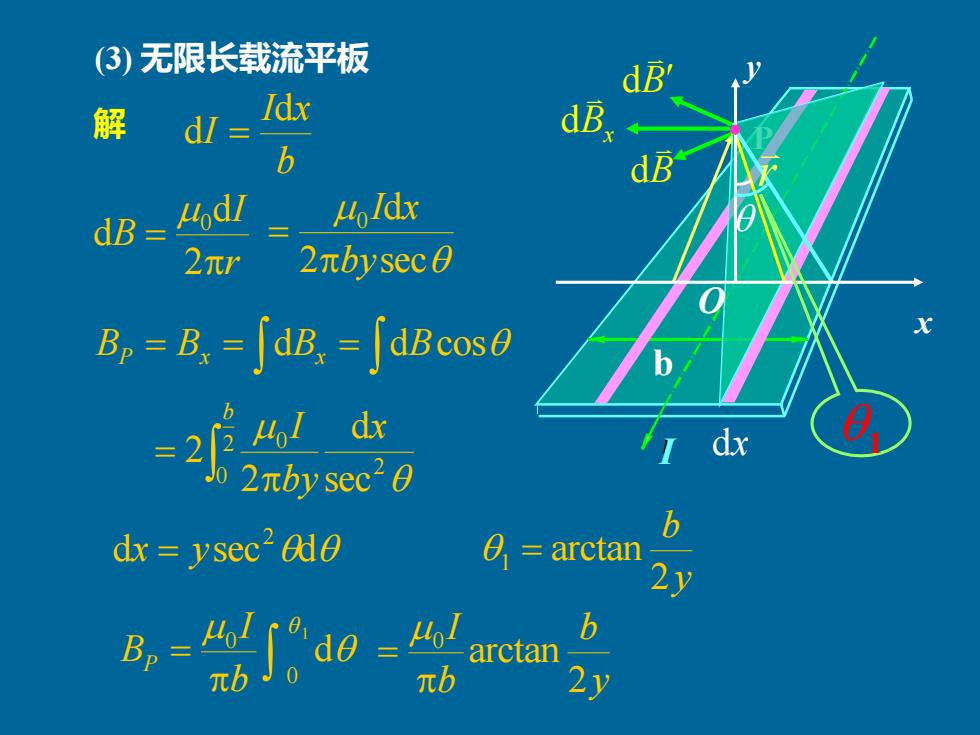
(③)无限长载流平板 解 Idx d/ dB. b dB dB d 461d 2π 2πbysec0 B,=B,=∫dB=∫dBcos0 。 dx dx ysec2ade 0 arctan 21 0=4 b arctan
I b (3) 无限长载流平板 P B d Bx 解 d b I x I d d = r I B = 2 d d 0 BP = Bx = Bx d = dBcos = 1 0 0 d θ P b I B y b b I 2 arctan 0 = d sec d 2 x = y r 2 sec d 0 by I x = = 2 0 2 0 sec d 2 2 b x by I x y O dx y b 2 1 = arctan B d 1
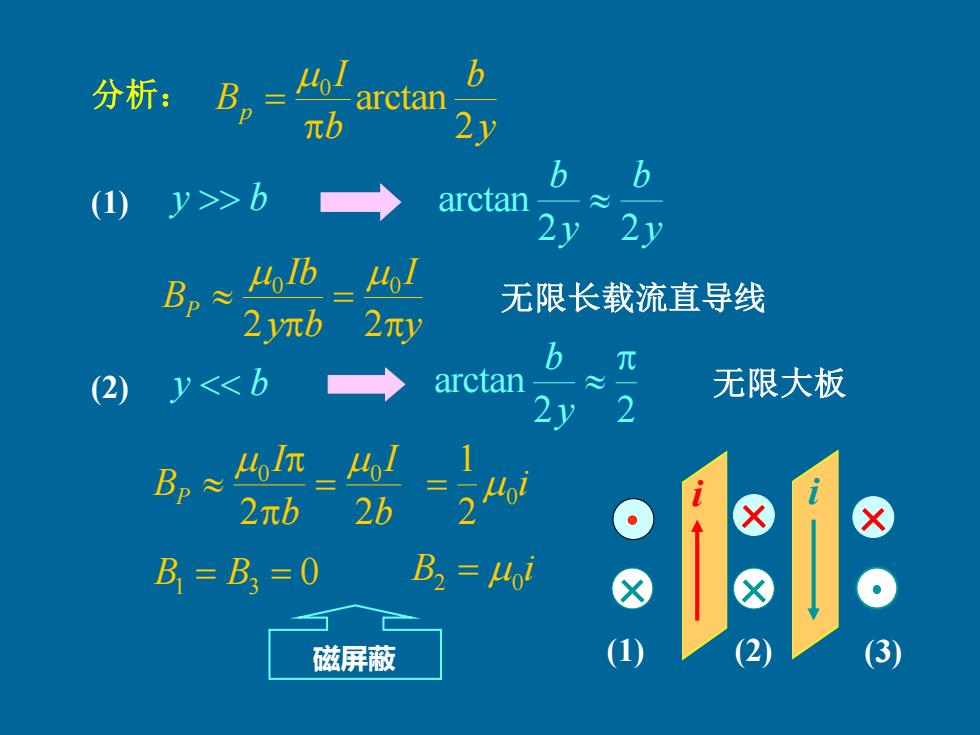
b 分析: B =o! arctan πb 2y (1) y>>b arctan 无限长载流直导线 2yπb b (2 <<6 arctan 无限大板 2y B2≈ 4π 41 2πb B=B3=0 B2=4o1 磁屏蔽 3
(1) (2) (3) 分析: y b b I Bp 2 arctan 0 = (1) y b y I y b Ib BP = 2 2 0 0 y b y b 2 2 arctan 无限长载流直导线 (2) y b 2 2 arctan y b b I b I BP 2 2 0 0 = i 0 2 1 = 无限大板 0 B1 = B3 = B i 2 = 0 磁屏蔽 i i