
分类问题2 1
分类问题2 1

Outline ·4.3补充:优化算法NNDL《神经网络与深度学习 》附录p418-425 ·4.3支持向量机 哈尔滨工业大学计算机学院刘远超 2
Outline • 4.3 补充:优化算法NNDL《神经⽹络与深度学习 》附录p418-425 • 4.3 ⽀持向量机 哈尔滨工业大学计算机学院 刘远超 2

数学优化的类型 ·离散优化(Discrete Optimization) ·组合优化(Combinatorial Optimization) ·整数规划(Integer Programming) ·连续优化(Continuous Optimization) ·无约束优化(Unconstrained Optimization) ·约束优化(Constrained Optimization) ·线性规划(Linear Programming) ·非线性规划(Nonlinear Programming) ·凸优化(Convex Optimization) 哈尔滨工业大学计算机学院刘远超 3
数学优化的类型 • 离散优化(Discrete Optimization) • 组合优化(Combinatorial Optimization) • 整数规划(Integer Programming) • 连续优化 (Continuous Optimization) • ⽆约束优化(Unconstrained Optimization) • 约束优化(Constrained Optimization) • 线性规划(Linear Programming) • ⾮线性规划(Nonlinear Programming) • 凸优化(Convex Optimization) 哈尔滨工业大学计算机学院 刘远超 3
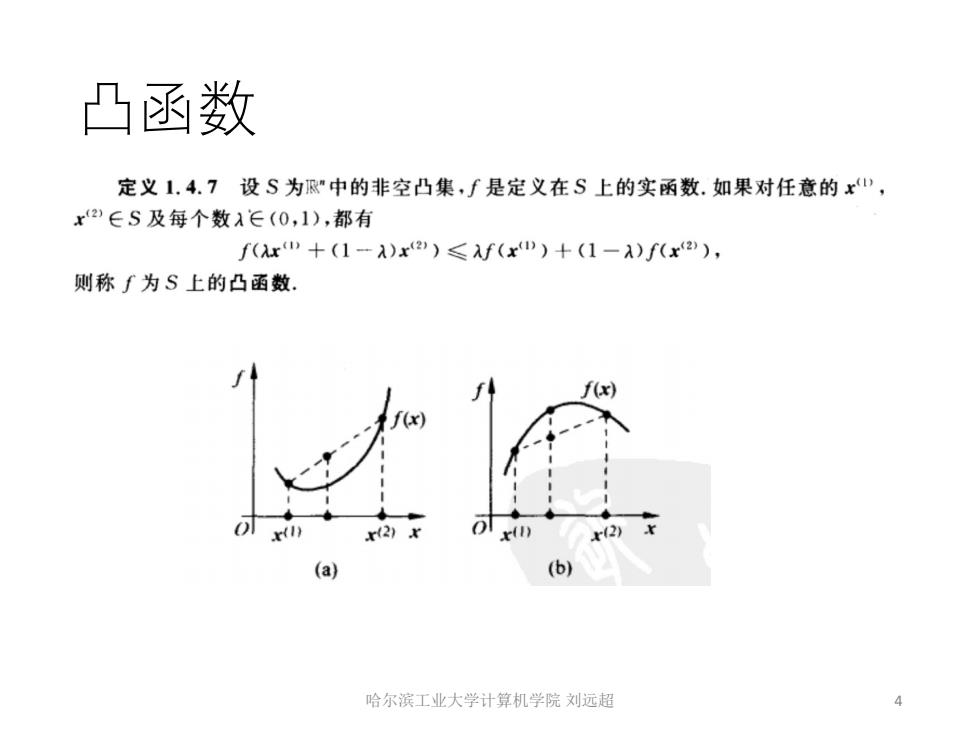
凸函数 定义1.4.7设S为"中的非空凸集,f是定义在S上的实函数.如果对任意的x”, x2∈S及每个数1∈(0,1),都有 f(x+(1-A)x2)≤f(x)+(1-A)f(x2), 则称f为S上的凸函数 f(x) (x) x(2)x ol xin r2) (a) (b) 哈尔滨工业大学计算机学院刘远超 4
凸函数 哈尔滨工业大学计算机学院 刘远超 4
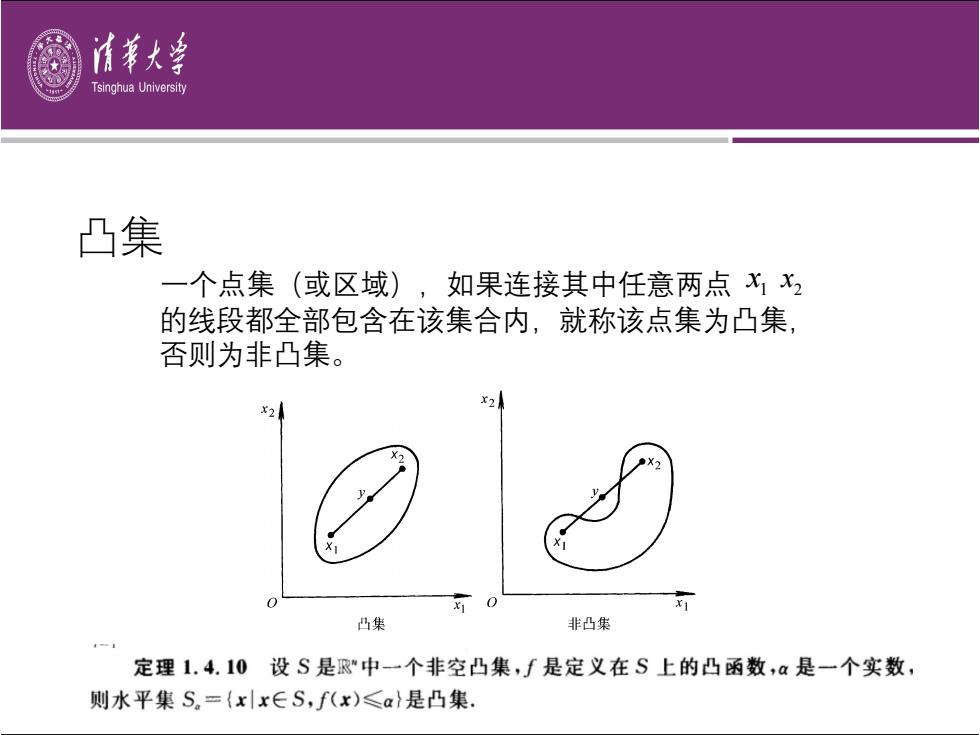
清蒂大学 Tsinghua University 凸集 一个点集(或区域),如果连接其中任意两点xx2 的线段都全部包含在该集合内,就称该点集为凸集, 否则为非凸集。 X2 凸集 非凸集 定理1.4.10设S是歌"中一个非空凸集,f是定义在S上的凸函数,a是一个实数, 则水平集S。={xx∈S,f(x)≤a}是凸集
的线段都全部包含在该集合内,就称该点集为凸集, 否则为⾮凸集。 ⼀个点集(或区域),如果连接其中任意两点 1 x 2 x 凸集