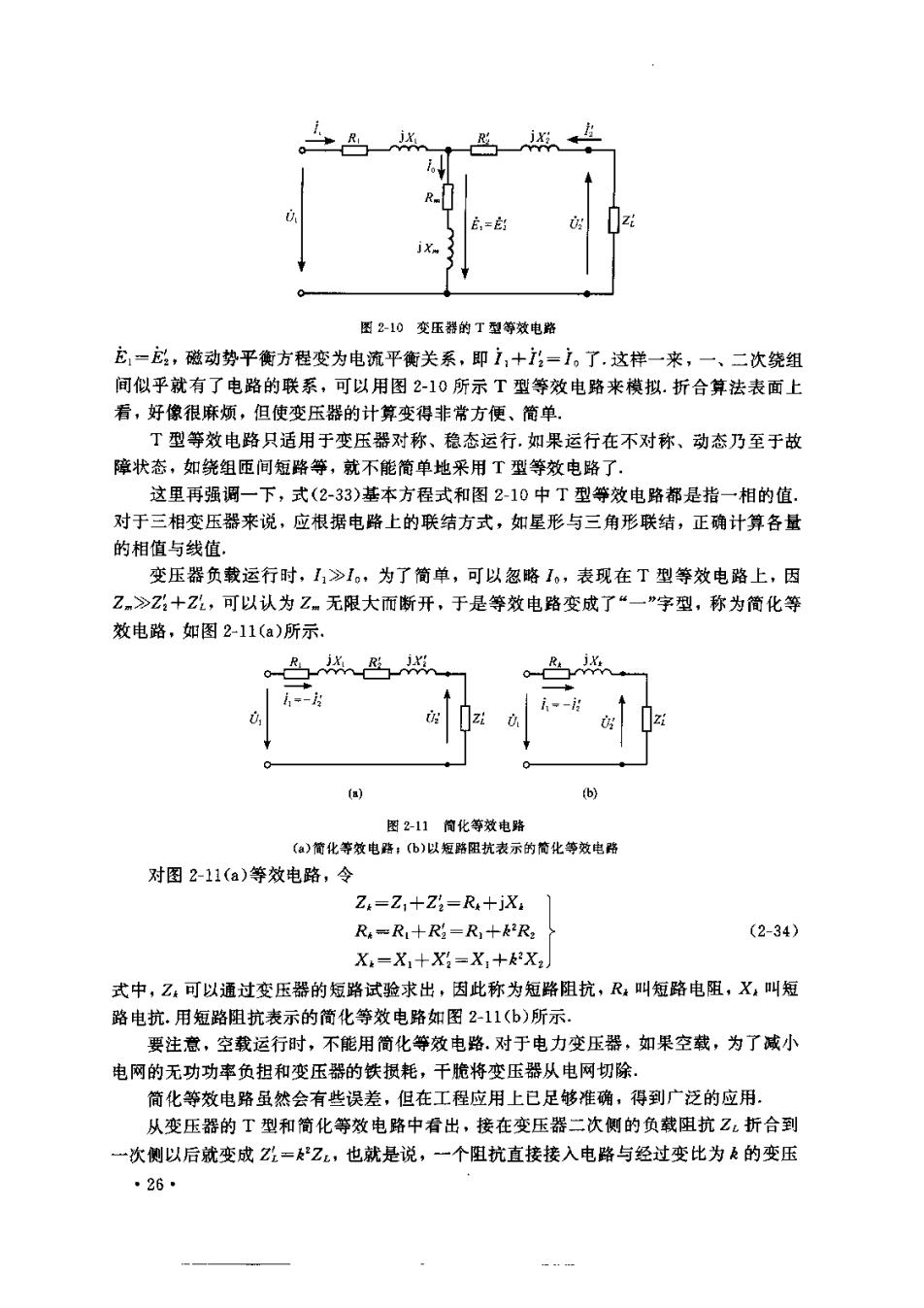
图?10变压器的T型等效电路 龙,-,磁动势平衡方程变为电流平衡关系,即1,+:-。了.这样一来,一、二次绕组 间似乎就有了电路的联系,可以用图2-10所示T壅等效电路来模拟.折合算法表面上 看,好像很麻烦,但使变压器的计算变得非常方便、简单, T型等效电路只适用于变压器对称、稳态运行,如果运行在不对称、动态乃至于故 障状态,如绕组匝间短路等,就不能简单地采用T型等效电路了, 这里再强调一下,式(2-33)基本方程式和图2-10中T型等效电路都是指一相的值 对于三相变压器来说,应根据电路上的联结方式,如星形与三角形联结,正确计算各量 的相值与线值. 变压器负载运行时,1》1。,为了简单,可以忽略1。,表现在T型等效电路上,因 Z>+2弘,可以认为乙。无限大而断开,于是等效电路变成了“一”字型,称为简化等 效电路,如图211(a)所示. 2-11筒化第效电路 6简化等效电路 )以短 粗抗表示的简化等效电路 对图2-11(a)等效电路,令 Z=Z:+Z=R,+iX. R,=R,+R2=R,+k2R, (2-34】 X=X+X=X+X 式中,乙:可以通过变压器的短路试验求出,因此称为短路阻抗,R叫短路电阻,X,叫短 路电抗.用短路阻抗表示的简化等效电路如图2-11(b)所示 要注意,空载运行时,不能用简化等效电路.对于电力变压器,如果空载,为了减小 电网的无功功率负担和变压器的铁损耗,干脆将变压器从电网切除 简化等效电路虽然会有些误差,但在工程应用上已足够准确,得到广泛的应用. 从变压器的T型和简化等效电路中看出,接在变压器二次侧的负载阻抗Z,折合到 一次侧以后就变成Z=Z,也就是说,一个阻抗直接接入电路与经过变比为®的变压 ·26

器接入电路,对电路而言,二者的数值就差了倍。这就是变压器变阻抗的作用.例如 在电子学中,带一只扬声器的功率放大器,为了能够输出尽可能的最大功率,需要一定 的负载阻抗值,而扬声器线圈的阻抗数值往往又与需要的数值相差太远,直接接上去, 输出功率太小,因此,就采用在功率放大器与扬声器之间接一个输出变压器,来实现扬 声器阻抗变换,达到最大的功率输出,这就是阻抗匹配 前面讨论折合算法时曾提到,也可以把一次绕组折合到二次绕组匝数的基础上.这 样,二次各县都用实际值,一次各量都加“”,为折合值.如果还用同一变比是=N/Nz, 则一次各量分别为 R=R,X=点x, R=京R·X=X, 0=0,i=i,6=ei 6.相量图 根据变压器折合后的基本方程式(233)及T型等效电路或简化等效电路,可以画出 变压器负载运行的相量图. 变压器接感性负载,即负载阻抗由电阻和电感组成,c3即cos为滞后的功率因 数,此时的6个基本方程式及T型等效电路画出的相量图见图2-12(a).图212(b)为接 容性负载(即负载阻抗由电阻和电容组成,c0s4为超前的功率因数)时的相量图.为了清 楚起见,图中各漏阻抗压降及励磁电流1。的相量都做了夸大,实际上U,与E:大小相差 不多,U与E:大小也相差不多. 相量图的画法要视变压器所给定的及求解的具体条件而定.给定量和求解量不同 画图步骤也不一样.例如,若给定U、12,c0s%、及各个参数,画图步骤为:(1)画出 心和,其夹角为,这里要注意负载是感性的,还是容性的,才能正确画出:与 哪一个超前,哪一个滞后,(2)在相量上,如上:,再加上X:得出,(3) 它,=:(4)画出超前它,90的主磁通本.:(5)根据1。=一龙/2.,画出i。,它超前中. 个铁耗角;(6)画出(-:),它与1。的相量和为1:(7)画出(一E),加上i,R,再加上 iX,得到0.通过以上7步,完成了相量图.画相量图的步骤可以不同,但是,每一步 或每画一个相量,都依据着相应的基本方程式,相量图是基本方程式的体现,或者说是 基本方程式的图形表示法.6个基本方程式都在图上表示清楚了,相量图也就画完了,其 结果并不因画图步不同而有什么变化. 从图2-12相量图中看出,变压器一次电压0,与电流1的夹角为9,称为变压器负 载运行的功率因数角,c$9为功率因数.对于运行着的变压器,负载的性质和大小决定 了0,是超前还是滞后于1,决定了9的数值以及cos%的大小.实际上,由于1《1 1《U1,1,Z,<U,cos的数值接近于cos%,图2-12中由于夸大了1,、1和i2 相量,这一关系不明显, ·27
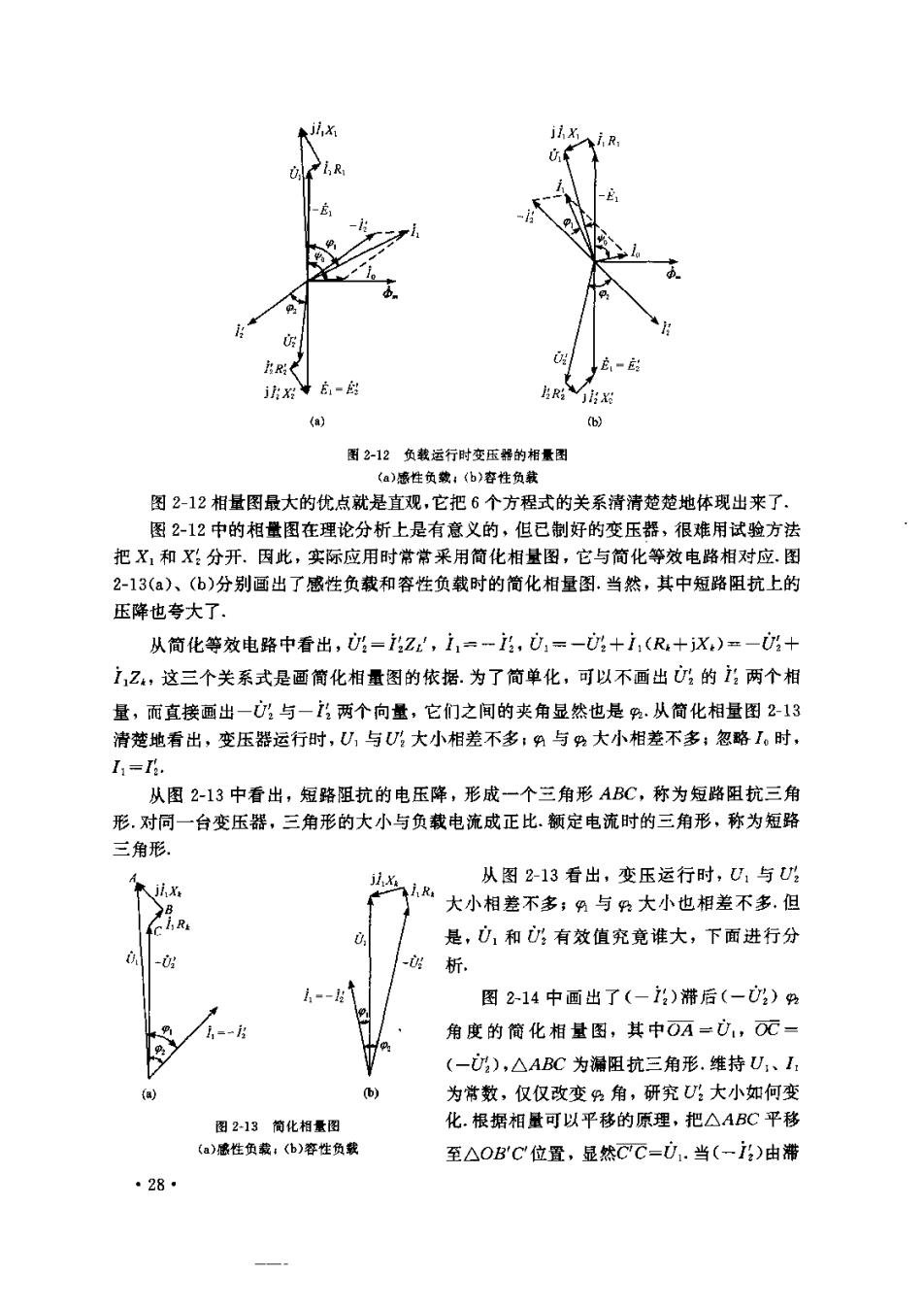
图212负载运行时变压释的相景图 (a)感性负救:《化)容性负载 图2-12相量图最大的优点就是直观,它把6个方程式的关系清清楚楚地体现出来了」 图2-12中的相量图在理论分析上是有意义的,但已制好的变压器,很难用试验方法 把X,和:分开.因此,实际应用时常常采用简化相量图,它与简化等效电路相对应.图 2-13(a)、(b)分别面出了感性负载和容性负载时的简化相量图.当然,其中短路阻抗上的 压降也夸大了. 从简化等效电路中看出,=Z,1=一,0,=-:+,(R+X)=一+ ,乙4,这三个关系式是画简化相量图的依据.为了简单化,可以不画出:的:两个相 量,而直接画出一与一:两个向量,它们之间的夹角显然也是.从简化相量图213 清楚地看出,变压器运行时,山与大小相差不多:与9大小相差不多:忽略1。时, I=. 从图2-13中看出,短路阻抗的电压降,形成一个兰角形ABC,称为短路阻抗三角 形.对同一台变压器,三角形的大小与负载电流成正比、额定电流时的三角形,称为短路 三角形 从图2-13看出,变压运行时,1与 ji R 大小相差不多:与大小也相差不多,但 是,心,和有效值究竟谁大,下面进行分 析. 图2-14中画出了(-)滞后(-0)% 角度的简化相量图,其中OA=心,OC (-),△ABC为漏阻抗三角形.维持U:、1 为常数,仅仅改变马角,研究大小如何变 图213筒化相B 化.根据相量可以平移的原理,把△ABC平移 少性负载 6)性负我 至△OBC位置,显然CC=U.当(-i)由滞 28

后逐渐变为超前(-)时,由于U1大小不变,0,端点轨迹在以0为圆心、以OA为半径 的圆周上.又由于(一:)有效值不变,△ABC大小不变,只能平移,但不管移到哪里,最 终都能移至△OBC处,从而使CC的长短不变.可见,相量(一:)的端点轨迹是以C为 圆心,以CC为半径的圆周上(见图2-14).例如,当(一)超前(一)4时,A点移至 A:,△ABC移至△AB,C,这时,CC-D1,OC-(-),这时U5>U.在图2-14中 的。点,U=U.接在电力系统的变压器,空载时,输电线之间及输电线对地电容,对变 压器来说,相当于带了超前性负载,有可能抬高二次电压。 图2-14变压器橙潘后安超前性负栽二次端电玉惭迹 至此,我们介绍了分析计算变压器负载运行的基本公式、等效电路和相量图,三者 都能各自独立地表示变压器在一定条件下运行时各个电磁量之间的关系,既可分别独立 使用,也可以联合使用。 7.功率关系 将式(222)两边与定子电流相量11取点积(标量积),得 0,·i1=(-E)·i1+[i,(R+ix1)]·i1 =(-E)·(i。-ii)+R =R+:·i+R. (2-35) 上式为,一次侧输入功率一铁损耗十传给二次侧的电磁功率十一次铜损耗 将式(227)两边与电流1:取点积,得 ·i=·i-[i(+x)]· =·i-2R4 (2-36) 上式为,二次侧输出功率一一次侧传递给二次侧的电磁功率十二次铜损耗 将式(2-36)代入式(2-35),得 01·i1-I8R+1R-1R'=0·i U,I:cos-IiR-IiR:-IiR:=U;Ficosg (2-37) 上式为,变压器一次侧输入的电功率减去本身各种损耗,包括铁损耗,一、二次铜损耗, 才是二次侧输出给负载的电功率 ·29·

关于无功功率,将式(2-22)两边与电流,取叉积,得 0,×i1=(-E)×i+[i,(R+ijX)门×i -(-E)×(i。-i)+x =Xx+ (2-38) 将式(226)两边与电流取叉积,得 ×1:=E:×-[i(R%+iX)]× =×-X: (2-39) 将式(2-39)代入式(2-38),得 UI,sing-IiX.-IiX-I'X:-Uilising 如染变压器二次侧接的是感性负载,则一次侧从电源吸收滞后性无功功率,减去励 磁电抗,一、二次漏电抗上需要的无功,余下的则供给二次侧负载所需要的无功功率, $2-4标么值 在变压器和电机里,各物理量的大小,除了用它们各自的计量单位表示外,还可用 标名值来表示.所调标么值,就是某一个物理量的实际值与选定一个同单位的固定数值 进行比较,它们的比值就是这个物理量的标么值,把选定同单位的固定数值称为基值。 实际值(任意单位) 标么值一素值(与实际值同单位) 例如,有两个电压:U1=99V:U2-11kV,如果选110kV作为电压的基值时,这 两个电压用标么值表示,用U和U表示,即 &-0-器=1.0 这就是说,电压U1是所选基值110kV的0.9倍:电压,是基值的1倍. 既然各物理量用标么值表示时,都要被各自选定的基值去除,所以,选基值就显得 很重要了.在变压器和电机里,一般都选额定值作为自已的基值.关于选基值的个数,不 是任意的,还应注意各基值之间的一定联系.例如,对单相变压器,选额定电压、额定电 流分别作为基值,其容量(或功率)和阻抗的基值就不能任意选择.容量(或功率)的基值 用Sw表示,为 Sx=UNIN 阻抗的基值用zw表示,为 对三相变压器,选额定线电压、新定线电流分别作为基值,其容量(或功率)的基值 为 Sw=√/3Uwlx 30·